机床热误差的检测与建模方法

赵万芹， 刘昊栋， 施 虎

(1.西安交通大学， 机械制造系统国家重点实验室， 西安 710049； 2.上海工程技术大学材料工程学院， 上海 201620)

随着制造业的迅速发展，机床作为制造业的基础，对其加工速度和精度提出了更高的要求。热误差是影响机床加工性能的重要因素，已成为机床加工误差的最大误差源，占比达40%～70%[1-2]。要提高机床加工精度，需要对机床热误差进行控制，主要包括：误差防止法和误差补偿法[3-4]。前者主要通过减少热源数目或降低热源热量，增加散热路径，以及采用热稳定结构设计等方法来控制机床热误差[5]，是对机床硬件的设计和制造过程进行改进，因此又称为硬件补偿法，该方法可以在一定程度上降低热源温升、均衡温度场和减少机床热变形，但是补偿成本高且补偿效果不明显，具有很大的局限性[6]。后者即误差补偿法也称为软件补偿法，其主要机制为通过软件输入人为制造新的逆方向误差，削弱甚至抵消原始误差[7]，该方法无需对机床进行硬件上的改造，却可使被加工工件精度显著提高，较热误差防止法具有高柔性、高经济性的优势，因此在机械加工业中受到越来越广泛的重视，并且已作为国际上提高数控机床精度的主要方法[8-9]。在误差补偿法中，获得机床热误差并建立热误差模型是整个补偿过程的核心与关键。现对热误差补偿过程中上述两项重要步骤展开叙述，论述了机床热误差的检测方法和建模方法，并结合目前的研究现状，展望了未来的发展。

1 机床热误差的检测方法

机床热误差的检测在整个误差补偿环节中有着相当重要的作用，检测目的是对机床原始误差参数进行精确测定，准确、快速、稳定地实现机床热误差的检测是进行热误差建模、补偿的基础和前提[10]。机床热误差的检测方式通常可以分为：直接法和间接法。

1.1 直接检测法

直接检测法是通过各类仪器对热误差直接测量，通过表盘或显示界面可直接得到机床某个部件产生的热误差数值，因其测量方式简便且精度较高，目前应用较为广泛。直接检测法的检测装置主要包括传统测量仪器、位移传感器、激光干涉仪等。需要说明的是，在采用直接检测法对热误差进行检测前，首先需要明确热误差的表现形式，目的是明确热误差的研究对象并确定机床的检测部位。由于机床的不均匀温升，致使某些温升明显的部件尺寸发生变化或同其他部件的相对位置改变，具体可表现为主轴变形，床身及立柱的热膨胀变形，丝杠的膨胀，工作台的变形等众多方面[11]，其中，作为影响机床加工精度的最主要因素，主轴变形可以分解为轴向伸长，X、Y向热漂移，X、Y向热倾斜[12]，如图1所示。

直接检测法中传统的热误差检测工具包括直角尺、千分表、水平仪等，这一类仪器具有价格较低、操作简单等优点，测量结果可通过表盘读数直接获得，故在工厂实际测量中应用较为广泛[10]。阳红等[13]在丝杠前端安装百分表测量丝杠前端热变形；Umezu等[14]利用千分表来测量主轴和夹具间的位移，得到了立式加工中心的主轴X、Y向热倾斜夹角，并进行了各测点温度与热倾斜夹角的相关性分析。虽然传统检测工具检测过程简便，但由于其采用机械测量的方式，除去测量设备自身精度的限制，测量精度还会因人为误差的存在而降低，因此应用场合受限，故近年来逐渐被学者们淘汰。

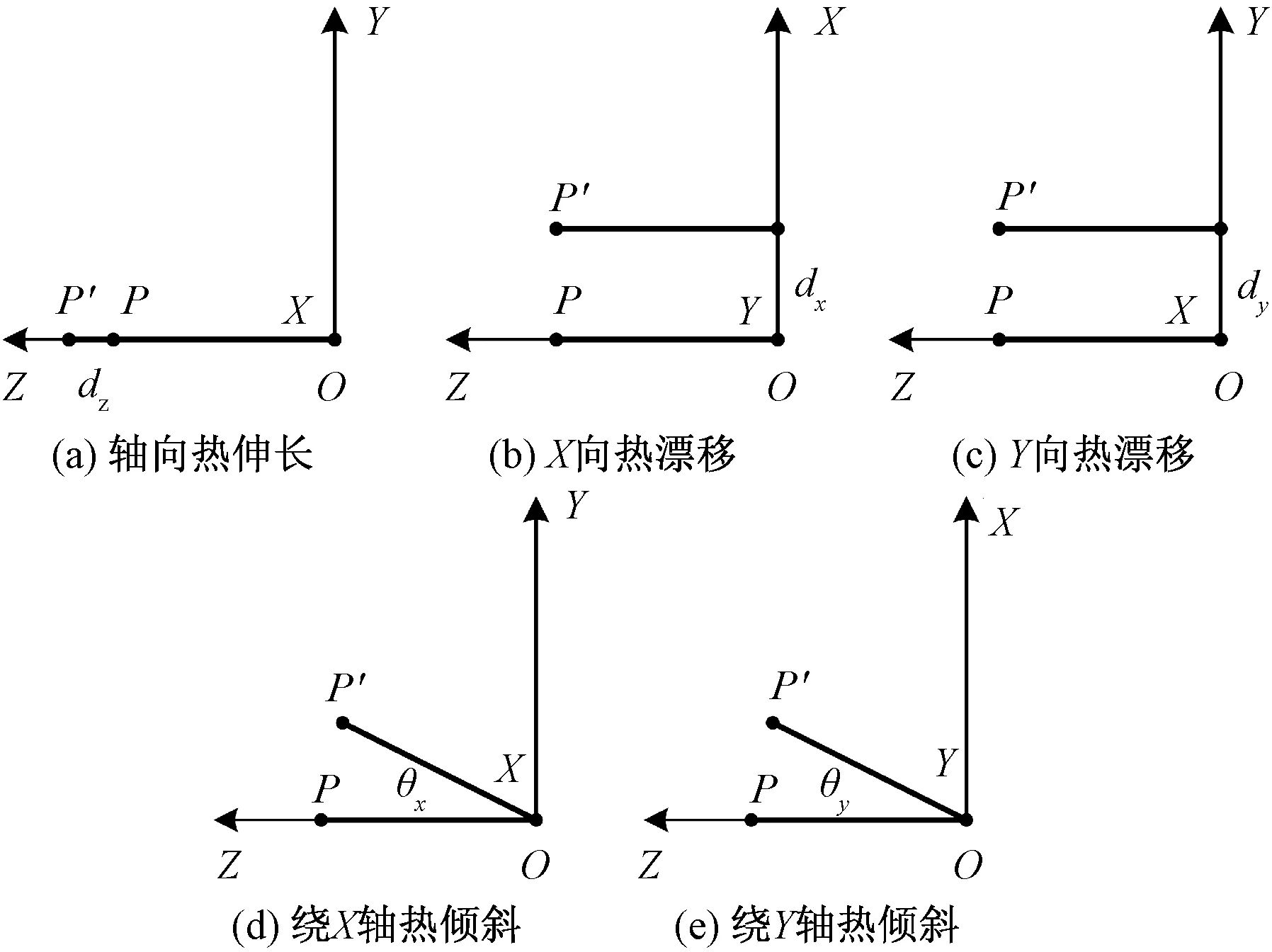
dx、dy分别表示主轴X向和Y向的热漂移量；dz表示主轴轴向 热伸长量；P、P′分别表示变形前和变形后主轴端部的位置；θx和θy 分别表示主轴绕X轴和Y轴的热倾斜角度图1 主轴热变形[12]Fig.1 Thermal deformation of spindle[12]

与传统热误差检测工具不同，位移传感器是通过非接触的方式来测量，还可以直接测量旋转轴的状态，且其有高灵敏性、强抗干扰性、可长时间稳定工作的特点，常用的位移传感器有电涡流位移传感器和激光CCD(charge coupled device)位移传感器等。张腰等[15]使用电涡流位移传感器测量立式加工中心Z向热误差变形量，获取了随该机床的温度变化与对应热变形变化的规律；张子祥等[16]将激光CCD位移传感器安装于镗铣床的主轴Y向和Z向的平行位置，直接测量镗轴两个方向的热误差数据，得到了热误差随时间变化的曲线，如图2(a)所示，比对后选取了主导误差Z轴误差作为研究对象。虽然位移传感器有众多优点，但每种传感器都有其局限性，如电涡流位移传感器量程不大，为±500 μm；激光CCD位移传感器体积较大，某些狭小空间安装极为不便甚至无法使用。上述问题致使各类位移传感器应用场合不同，需根据具体实验环境选择合适的传感器。曹永洁等[17]结合主轴工作环境设计了热误差检测系统，用于测量机床主轴工作时的热变形，热误差检测装置如图2(b)所示，其中，两个激光CCD位移传感器分别与检验棒X、Y向平行，测量X、Y向的主轴热变形，电涡流位移传感器置于检验棒下方，测量主轴轴向热伸长。

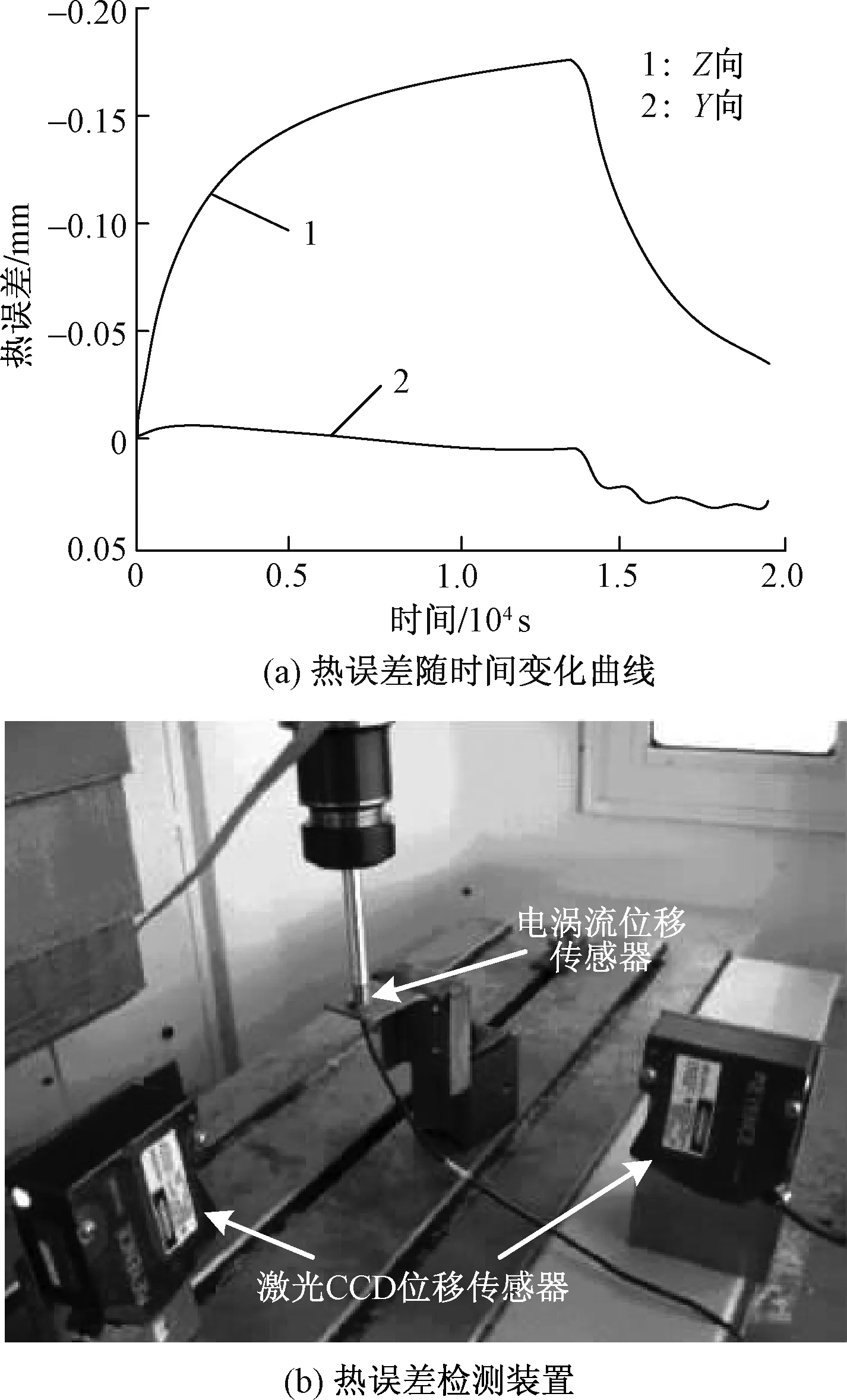
图2 热误差变化曲线及检测装置[16-17]Fig.2 The curve and the detection device of thermal error[16-17]

激光干涉仪因其采用非接触式测量的方式，且测量速度快、测量精度高，20世纪末期投入市场即受到了机床制造业的青睐[18]，众多学者将其应用于热误差的测量。林献坤等[19]使用两个双频激光干涉仪测量了进给轴的热变形量，该测量系统采集到的热误差和温度值一同作为样本库，为后续热误差模型建立提供数据。陈明等[20]采用激光干涉仪对某立式加工中心进给轴的热误差进行了测试，监测了进给轴近端、中端及远端不同热机时间的热误差变化，以用于同温升变化的分析。此外，任小洪等[21]在实时测量机床温度的同时采用激光干涉仪检测出对应时刻机床的热误差值，随后输入到模型中，通过数控系统(CNC系统)进行反馈补偿。虽然激光类仪器测量精度高，但其设备昂贵，光路调整困难且抗干扰性能较差，难以在高速加工过程中测量热误差[22]，故很多情况下将位移传感器与激光干涉仪配合使用。孙志超等[23]使用激光干涉仪测量车床进给轴热误差值同时使用电涡流位移传感器测量主轴热误差，将该机床主轴和进给轴耦合热误差建模补偿。

1.2 间接检测法

与直接检测法不同，间接法无法直接得出热误差的具体数值，而是经由其他媒介间接地反映出机床的热误差状况。常用的热误差间接检测法有两种：基于球杆仪检测法和试切法。

1982年，Bryan发明了可以测量机床动态精度的球杆仪，该装置由于测量简单便捷且精度补偿效果良好，现已被ISO 230国际机床检验标准推荐使用[10-24]。具体而言，球杆仪是通过两端的精密球的插补运动所形成的轨迹来判断热误差，将球杆仪的运动轨迹与标准圆进行比对，若与标准圆存在偏差，则误差存在，通过简单地辨识可以得到误差[25-27]，其测量原理如图3(a)所示。杨宝鹏等[28]基于如图3(b)所示的球杆仪实验装置，测量了不同时间段的机床主轴漂移误差。Delbressine等[29]利用球杆仪测量多轴机床的热漂移，并对该类机床建立了预测精度可达60%的通用热误差模型。虞敏等[30]基于球杆仪提出了一种热误差检测方法，通过将球杆仪运动轨迹设计为X、Y轴联动构成的圆锥体，建立杆长变化值与主轴热变形量之间的空间矢量几何关系，并以补偿实验进行了验证。尽管球杆仪检测过程简单，但其只能在较小空间内测量误差，且其安装时会存在原始误差，可采取一定措施减小但无法完全避免。

图3 球杆仪测量原理及实验装置Fig.3 The measuring principle and the experimental device of ball bar

直接检测法和基于球杆仪的热误差检测过程中，普遍是使机床空转来模拟加工时地状态，上述方法忽略了加工过程中的刀具磨损变形等因素的影响，而试切法是通过机床真实加工出来工件的尺寸参数，与标准件进行比较分析，进而反推出机床产生的热误差。如齿轮加工精度与径向热误差存在函数关系，加工过程中测量齿轮M值(又称跨球尺寸或圆柱尺寸)间接得到蜗杆砂轮磨齿机的径向热误差[31]。以试切的方式进行热误差检测，能够更真实、准确地反映机床的加工精度，获得的热误差数据的可信度也较高。2012年，由中国中航工业成都飞机工业公司提出的S型检测试件具有众多零件的典型结构特征，能够有效检测机床加工精度，S型试件在ISO国际会议获得一致认可，并通过其作为标准试件的草案[32]。虽然间接检测法能够反映机床真实加工时的精度状况，但该方法无法完成对整个加工系统的解耦与评估，且检验周期长、成本高。

综上所述，在选择机床热误差的测量方法时，要权衡直接和间接检测法的利弊，选择最优的方案来获取热误差数据，以保证能为接下来的机床热误差建模工作提供准确的数值。

2 机床热误差的建模方法

机床热误差建模是获取测点温度与热误差间关系的数学模型。热误差模型以测点温度为输入值，热误差为输出值，通过建立的模型，根据温度值便可预测机床即将发生的热变形。所以在热误差补偿中，建模技术是重点，热误差模型精度的优劣直接决定了机床加工精度的提升效果[33-34]。高预测精度与强鲁棒性是衡量热误差模型是否优异的标准，依据这个标准学者们寻找到了一系列建模法，如多元回归分析法、人工神经网络法、支持向量机法、灰色理论分析法及贝叶斯算法等。

2.1 多元回归分析法

多元回归分析(multiple regression analysis，MRA)是一种以单个或多个变量为输入、单一变量为输出的建模法，因该方法建立的模型具有高预测精度、高可靠性、表述简单等优点[35]，被广泛应用于各个领域，如医学[36]、自然科学[37]、统计学[38]等。基于多元回归分析法建立的机床热误差模型，以多个温度测点的温度值为自变量，以机床的热变形误差作为因变量，可以表示为[39-40]

Y=β0+β1X1+β2X2+···+βnXn+ε

(1)

式(1)中：Y为热变形误差；β0，β1，…，βn为自变量温度值的回归系数；ε为常数项；X1，X2，…，Xn为自变量温度值。

Chen等[41]于1993年首次将多元回归分析用于机床误差建模中，以进给轴工作位置与热误差间的函数方程进行了表示，模拟了热误差有关的11项误差。罗勇等[42]对NL201HA型数控卧式车床X轴进行了回归建模分析，在进行升温降温实验后绘制了热变形拟合曲线，如图4所示，其中，Δy为热误差增量，升温段模型误差预测值与实际值的最大拟合残差为4.8 μm，降温段模型的最大拟合残差为2.6 μm，预测效果较好。余蔚荔等[43]在筛选出最优的温度测点后，基于多元回归分析对铣床主轴建立了Y向、Z向热误差预测模型并进行了补偿，误差补偿后，Y向最大热误差值由45.0 μm减少到3.2 μm，Z向由28.0 μm减小到3.8 μm，机床精度得到明显提高。

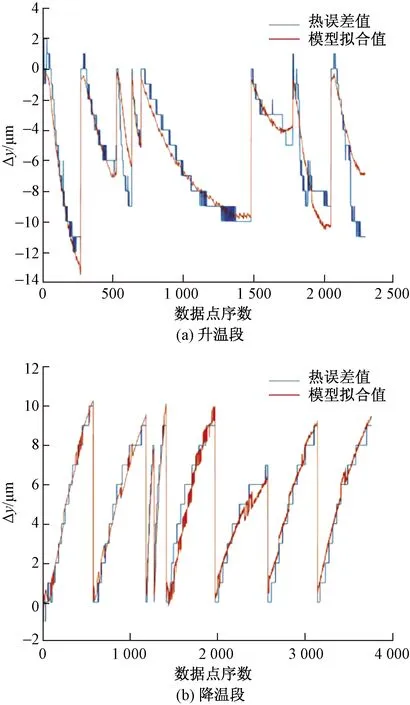
图4 线性回归模型拟合曲线[42]Fig.4 The fitting curve of linear regression model[42]

还需要说明的是，MRA模型对于结构、工况均为比较简单的机床具有较好的预测能力[44]，但在对模型系数选取时可能会与实际情况相反，使热误差模型稳定性降低，此外，模型构建时可能会出现超越方程，使得求解过程变复杂、运算的收敛性变差[45]。

2.2 人工神经网络法

人工神经网络(artificial neural network，ANN)是一种模仿人脑神经元对信息处理并组建网络的建模法。人工神经网络具有很强的逼近任意非线性函数的能力，且能够并行处理并存储数据，故该方法具有较强的鲁棒性和容错性[46-47]。

1986年，反向传播(back propagation，BP)神经网络由Rumelhart等[48]提出，BP神经网络作为一种误差反向传播的前馈型网络，现已成为应用最为广泛的ANN之一。图5展示了一个典型的三层神经网络的结构，分别为输入层、隐含层和输出层，在神经网络工作时，三层结构逐层处理输入的信号，当输出层的输出信号大于期望误差时，输入信号会进行反向传播，并自调整BP神经网络的权值和阈值，使模型输出可以不断接近期望输出[49]。

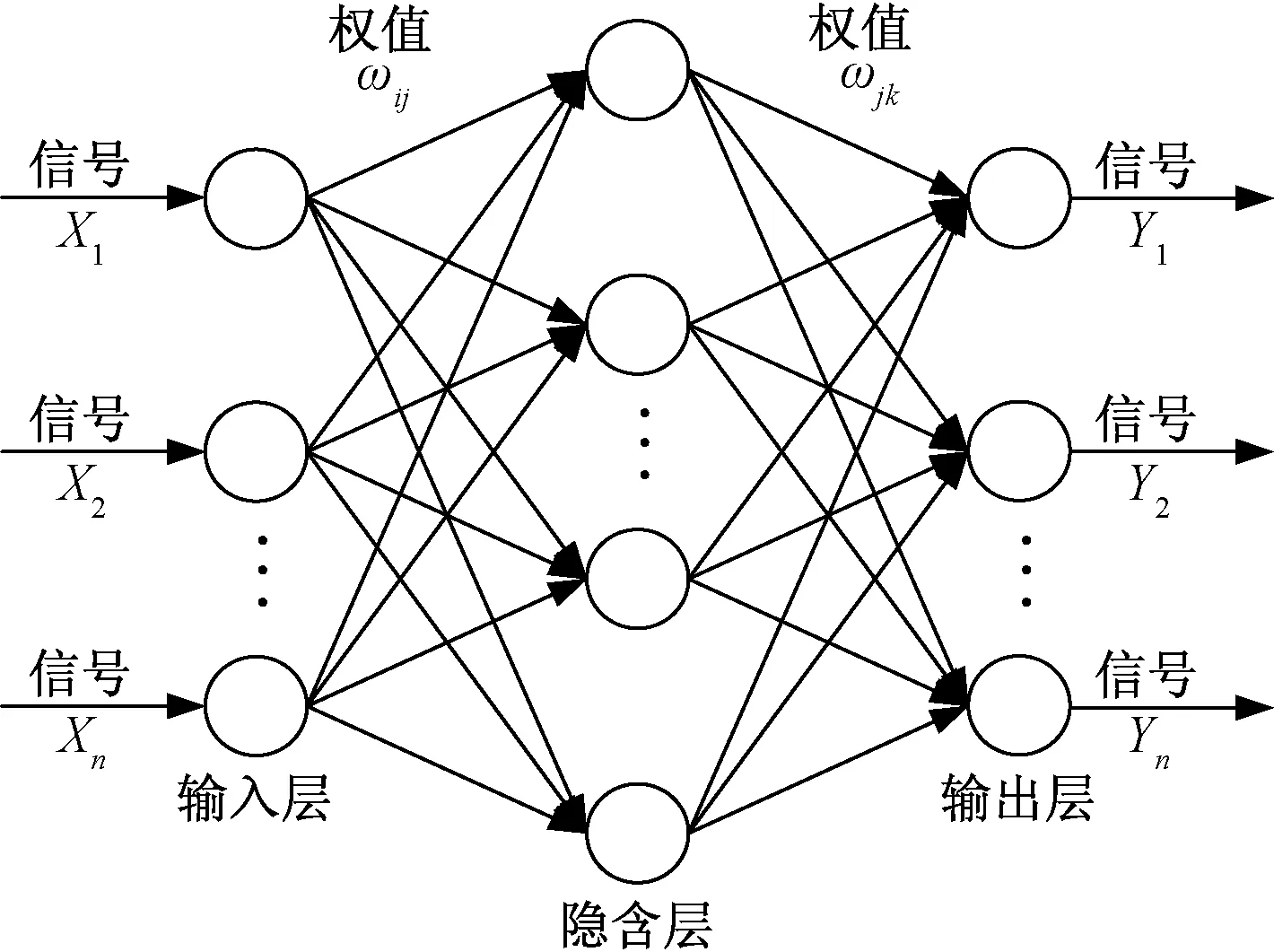
图5 BP神经网络结构Fig.5 The structure of the BP network

BP神经网虽然得到了广泛的应用，但它也存在不足之处，如收敛速度慢，训练时间长，有网络冗余性、遗忘性，存在局部极小、过度拟合等现象[50]。因此近年来学者往往将该建模方法进行预处理以避免其劣势。吴金文等[51]为避免BP网络产生局部极小值的问题，使用粒子群算法结合模拟退火法来优化了BP网络，对机床Y轴、Z轴方向进行了建模预测，优化前最大预测误差分别为7.3 μm和7.5 μm，优化后误差控制在3 μm以内，分别为2.3 μm和2.6 μm。

径向基函数(radial basis function,RBF)神经网络，同BP神经网络类似，同样有三层结构，输入层、隐含层和输出层，输入信号同样被输入层、隐含层和输出层逐层处理，不同的是，BP和RBF神经网络的隐含层不同，RBF神经网络的隐含层往往为径向基函数，该函数需要更多的神经元，但是它的训练速度也将更快，尤其是在输入信息样本数较大时，径向基神经网络往往能达到很好的效果[52]。陈松等[53]以5个测点温度作为模型输入值，建立了铣床主轴的RBF神经网络热误差预测模型，发现该模型预测值与实测值最大相差2.7 μm，且在导入补偿系统补偿后，最大热误差由43 μm减小到2.2 μm，大幅度提高机床精度。

ANN构建热误差模型时，虽然可以逼近任意非线性函数，但是很难选择使模型预测精度达到最优的网络结构，且因权值和阈值的不确定性，模型中可能会出现过拟合现象，此外，ANN模型往往需要较大的计算量，会增长反馈控制所需的时间，影响建模和补偿效率[54-55]。

2.3 支持向量机法

支持向量机(support vector machines，SVM)，于1964年由Vapnik等[56-57]提出，被认为是针对小样本统计和预测学习的最佳理论。该方法建模后的模型结构简单，有着较强的泛化能力，能处理少样本、非线性、高维数等问题，且能避免ANN中局部最优的问题，可以得到全局最优解[58-59]。

但由于支持向量机的核函数参数的选取会对模型精度有较大影响，因此核函数的选取至关重要[60]。林伟青等[61]率先将最小二乘支持向量机用于机床主轴热误差预测中，该方法的核函数为最小二乘线性系统，经建模和分析后，热误差预测值与热误差测量值的绝对百分比误差为1.88%，模型拟合精度高。刘善林等[62]基于支持向量机对数控加工中心不同时间的热误差进行预测，选取了高斯径向基作为其核函数，以第一批数据作为建模数据，并与多元回归模型进行了比对，如表1所示，发现当实际加工时的环境温度接近于模型预测时的环境温度时，支持向量机的预测精度远高于多元回归模型，在3、4月份的试验中，两种模型的预测精度相差不多，而当环境温度变化巨大时，多元回归模型的预测精度反而更高，由此也得出支持向量机对影响因素有着高敏感性，因此该模型的鲁棒性较差。

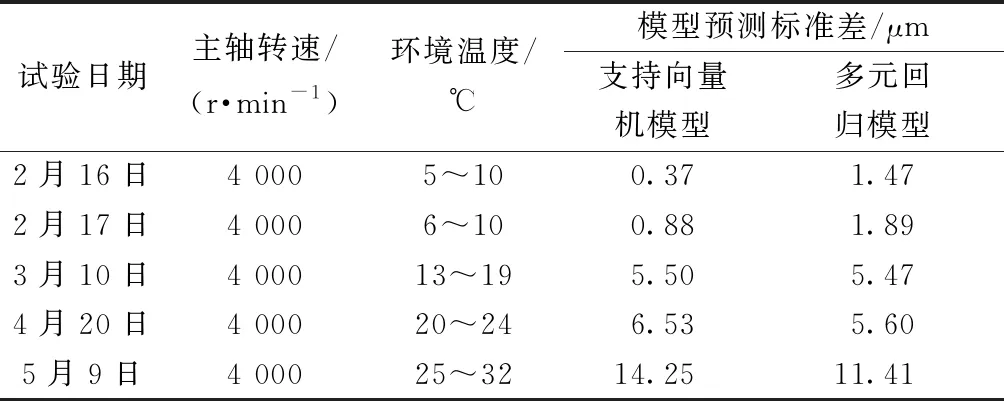
表1 5批试验参数的预测精度[62]Table 1 The prediction accuracy of five test parameters[62]

2.4 灰色系统理论法

灰色系统理论模型(grey system theory model，GM)是邓聚龙创立的灰色系统理论的核心内容，可对由数量少、无规律的样本组成的系统的内在发展规律进行描述[63-64]。2006年，李永祥等[65]应用三种灰色系统GM(1，1)模型进行了车床径向热误差的建模，三种模型分别为普通GM(1，1)模型、新信息GM(1，1)模型(只引入一个新变量)、新陈代谢GM(1，1)模型(每引入一个新变量，剔除一个旧变量)，建模前通过试验测量获取28组数据，将前18组进行建模，后10组进行验证，如表2所示，序号11为模型预测相对误差平均值，得出了灰色模型的预测优势，且随着新老数据的不断更替，模型预测效果会不断提高，最大相对误差只有13.51%。同样，李志伟[66]基于灰色理论模型突出的非线性拟合功能，对轮槽铣床主轴箱过建立灰色理论热误差预测模型，结果证明温度测点实测值与理论模型预测值接近，因此灰色理论模型具有准确性较好的预测水平。

表2 模型预测结果与测量值比较[65]Table 2 Comparison of model prediction results with measured values[65]

但与ANN相比，GM模型预测能力较弱，会因无关数据的存在或新旧数据的更替而对模型精度产生较大影响，且其并无自学习、自组织能力。因此，张毅等[67]提出了一种基于灰色理论预处理的人工神经网络机床热误差补偿模型(GM-ANN模型)，并将该模型的热误差和残差同GM模型和ANN模型进行了比对分析，分别如图6(a)、图6(b)所示，证实了GM-ANN模型的高预测精度，将车削中心的加工精度提高70%，有效弥补了GM模型和ANN模型的缺点。

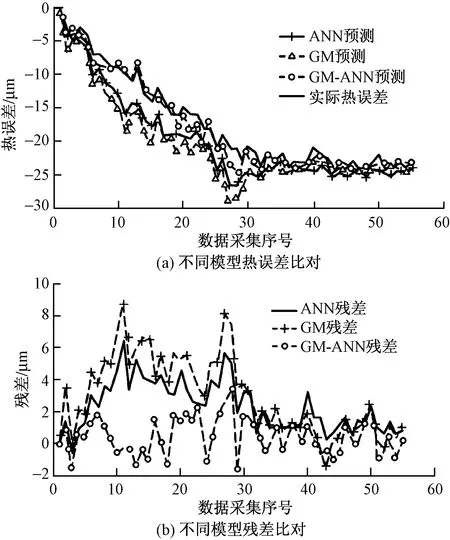
图6 GM-ANN、GM、ANN热误差和残差比对[67]Fig.6 The comparison of thermal error and residual value of GM-ANN, GM and ANN[67]

2.5 贝叶斯网络

1988年，Pearl[68]提出了贝叶斯网络(Bayesian network，BN)；2008年，白福友[69]率先利用贝叶斯网络对机床热误差进行建模。贝叶斯网络可以处理不完备数据集，相比于ANN，其优势在于解决复杂设备不确定性和关联性引起的问题，其模型建立流程如图7所示[70]，首先进行先验贝叶斯网络构造，随后基于样本数据进行学习与建模，最后基于贝叶斯网络的推理与热误差预测补偿。文献[70-72]基于贝叶斯网络进行了一系列探索，发现在热误差模型建立时，若只有较少的温度测点数据，则模型是以先验网络为主导，而随着温度测点数据的增多，模型预测更多地以数据为基础，符合认知规律。Shi等[73]经聚类和相关分析优化温度测点后，提出了一种基于贝叶斯神经网络的热误差建模方法，经试验证明该模型有着较高的预测精度，且在不同工况下，最大热误差从18.2 μm减小到5.14 μm，使进给驱动系统的热误差约减少了71%。但是BN同ANN一样，若想达到最优的预测效果，必须选择能够最为准确描述研究对象的网络结构，然而BN的网络结构复杂，且具有多项式复杂度，随着因素的增加，模型算法的复杂度将会呈指数型增长，极大的限制了BN的效果。

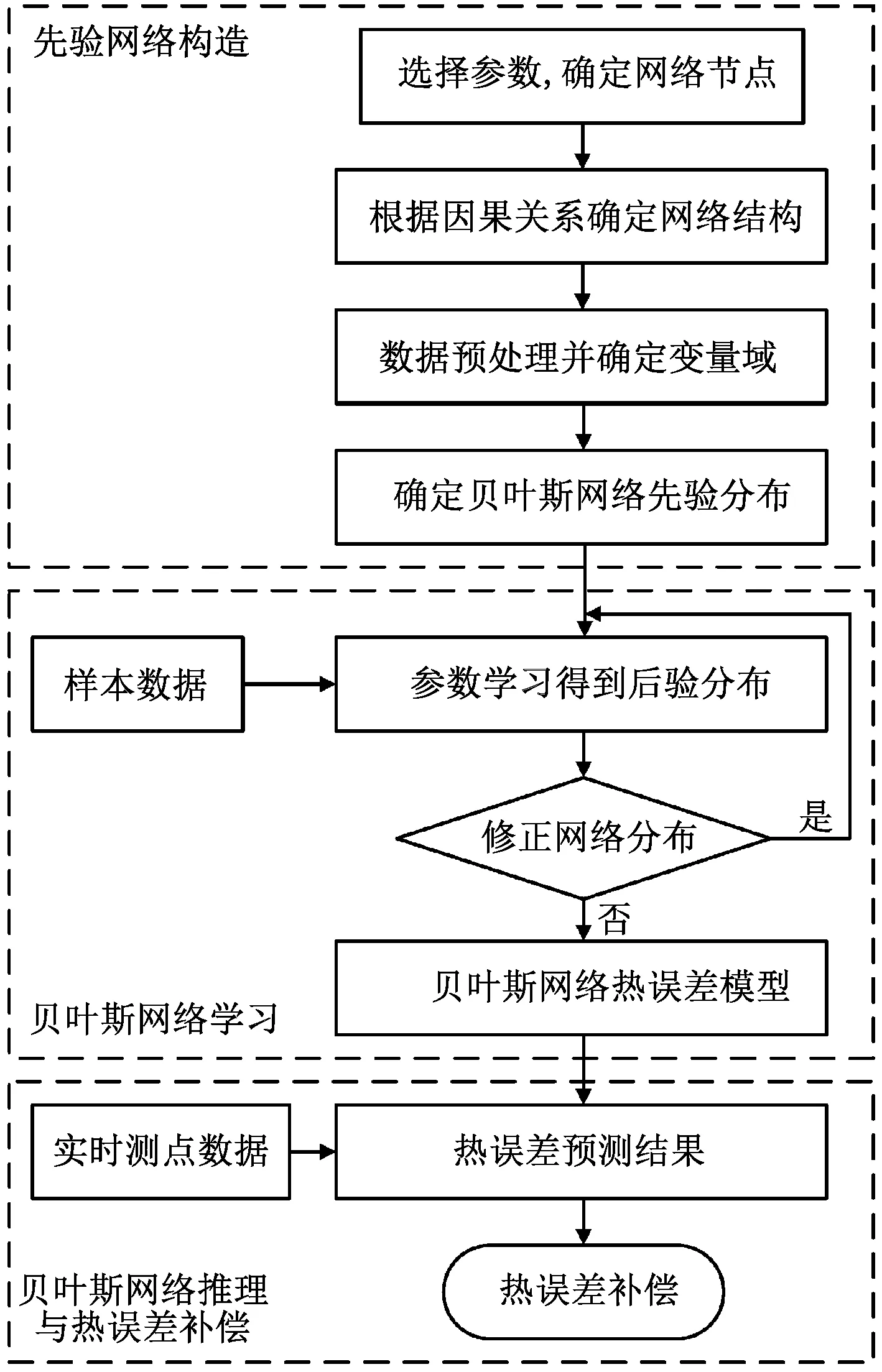
图7 贝叶斯网络建模流程图[70]Fig.7 The flowchart of Bayesian network modeling[70]

3 结论与展望

针对机床热误差补偿环节中的热误差检测方法和热误差建模方法展开叙述，得出如下主要结论。

(1)机床热误差的检测方法和工具颇多且各自都有独特的优点，但也都存在各自的限制，如传统测量工具测量精度不能保证，位移传感器安装会因机床内部环境而受限，激光干涉仪不能在高速加工条件下测量，球杆仪测量量程较小，试切法周期长、花费多，因此，实际测量中，需根据试验现场的工作状况选取一种或多种方法或工具的组合，以保证获取的热误差数据尽可能准确。

(2)机床热误差模型选择会很大程度上影响到热误差补偿的效果，五种方法所建立的热误差模型，都有着彼此无法替代的优势，也各有缺陷，表现为：MRA表述简单、预测精度高但可能会因超越方程的出现使运算变复杂；ANN能够自学习、自组织、自适应，却会存在过度拟合现象；SVM能对少样本的数据集进行有效预测，但模型鲁棒性较差；GM可以对无规律的样本进行预测，但预测精度较低；BN能够分析不完备的数据集并进行预测，但其网络模型难以确定。

(3)针对机床热误差的检测与建模方法，笔者认为还可以进一步探究：首先，误差防止法是从根本上控制热误差的方法，在机床设计阶段对其结构优化是至关重要的，除此之外，热误差检测时的安装空间受限等问题，也可在机床设计阶段得以解决，如适当增大内部空间，或机床内部增加自监控装置，能够实时检测机床温度和热误差状态。随着对机床精度要求的不断提高，单一预测模型的鲁棒性和其补偿后的精度无法满足补偿要求，对上述5类模型的优化仍是热误差建模研究中的热点。此外，5类模型中有的模型预测精度高，但需要较多参数和大量计算，有的模型只需少量样本和计算，但预测精度低，因此寻找到既满足高预测精度又只需少量数据，或能在二者间找到最优平衡的新模型，是热误差建模的研究方向之一。