基于IDA的铅黏弹性阻尼减震结构地震易损性研究

黄炜元 张超 周云 石菲

摘 要：为系统评估铅黏弹性阻尼器（Lead Viscoelastic Damper，LVD）减震设计钢筋混凝土框架结构的抗震性能，设计了8度（0.2g）地区的一栋6层钢筋混凝土抗震框架结构（Reinforced Concrete Frame，RCF）和铅黏弹性阻尼减震框架结构（LVD-damped Frame，LVDF）。使用OpenSees软件建立了RCF结构和LVDF结构的弹塑性分析模型，采用ATC-63推荐的22条远场地震动对RCF和LVDF进行增量动力分析，基于增量动力分析结果对其进行概率地震需求分析和地震易损性分析，定量評估了RCF结构和LVDF结构超越各损伤状态的概率。研究表明：铅黏弹性阻尼器可以有效控制结构地震动响应，使同一地震作用下LVDF结构的地震动响应小于RCF结构;由概率地震需求分析结果可知，铅黏弹性阻尼器可以降低因地震动特性差异导致的结构动力分析结果的离散性;由地震易损性分析结果可知，LVDF结构在不同损伤状态下的超越概率均低于RCF结构，表明铅黏弹性阻尼器可以显著降低结构的损伤，提高结构的抗震性能。

关键词：铅黏弹性阻尼器;增量动力分析;易损性分析;抗震性能;钢筋混凝土结构

中图分类号：TU375.4 文献标志码：A 文章编号：2096-6717（2021）03-0075-08

Abstract： To systematically evaluate seismic performance of reinforced concrete frame structure designed with lead viscoelastic damper （LVD）， a 6-layer RC frame （RCF） and LVD-damped RC frame （LVDF） in 8 degree （0.2g） were designed and established. Finite analysis models of the RCF and LVDF were built using OpenSees. Incremental dynamic analysis （IDA） was conducted to both RCF and LVDF using a total of 22 far field ground motion records as recommended from ATC-63. Based on results of IDA， probabilistic seismic demand analysis followed with the seismic fragility analysis was carried out for RCF and LVDF， and the probability of achieving different damage states of RCF and LVDF were quantitatively evaluated. The analysis results show that lead viscoelastic damper can be used to seismically control structural dynamic behavior so that structural response of LVDF is smaller than that of RCF under the same earthquake. As shown in results of probabilistic seismic demand analysis， LVD reduce dispersion of structural dynamic analysis results due to differences characteristics of ground motion records. As shown in seismic fragility analysis results， LVDF has lower probability of exceedance under different damage states than that of RCF， indicating that LVD can significantly both release structural damage and improve seismic performance of the structure.

Keywords： lead viscoelastic damper; incremental dynamic analysis; fragility analysis; seismic performance; reinforced concrete structure

历次震害调查发现，钢筋混凝土（RC）框架结构在强地震作用下损伤严重，甚至倒塌[1]。近年来，消能减震技术的发展和应用为降低主体结构损伤、提高结构抗震抗倒塌性能提供了有效可靠的技术支持[2]。铅黏弹性阻尼器由于具有铅芯屈服耗能和黏弹性材料剪切滞回耗能双重耗能机制共同耗能的优点，以及铅芯在常温下具备动态回复和再结晶的特点，且黏弹性材料在设计变形范围内具有超弹性的特性[3]，具有优异的耗能能力，在既有建筑的抗震加固和新建建筑的抗震与抗风设计中均有广泛的应用前景。目前，铅黏弹性阻尼器的研究主要集中在阻尼器力学性能和减震结构抗震性能的提升，对铅黏弹性阻尼减震结构抗震性能的系统评估对推动铅黏弹性阻尼器的发展和应用具有重大意义[4]。

地震易损性作为基于性能的地震工程是重要一环，表征结构在不同强度水平的地震作用下发生不同极限状态破坏的超越概率，可以从概率角度量化地震动和结构的不确定性对结构抗震性能的影响[5]。

介绍了基于IDA方法的地震易损性分析方法，设计并建立了一栋6层RC抗震结构（RCF）和铅黏弹性阻尼减震结构（LVDF）的有限元模型，采用ATC-63推荐的22条远场地震动对该结构进行IDA分析和地震易损性分析，定量评估该结构达到各极限状态的概率。

1 基于IDA的地震易损性分析方法

1.1 IDA基本原理

增量动力分析（Incremental Dynamic Analysis，IDA）广泛用于结构抗震性能评估，可量化评估结构的地震易损性[6]。IDA方法通过将一系列按一定比例系数进行缩放的地震动分别作用于结构，得到结构的非线性时程响应及结构损伤指标（Damage Measure，DM）和地震动强度指标（Intensity Measure，IM）之间的关系曲线，即IDA曲线[7]。

1.2 地震动选取

美国应用技术委员会在ATC-63报告[6]中给出的22条远场地震动记录较好地考虑了地震动的峰值、频谱特性和持时等地震动不确定因素对结构响应的影响，因此，选取这22条地震动记录对RCF结构和LVDF结构进行IDA分析。

1.3 地震动强度指标和结构损伤指标

合理选取地震动强度指标和结构损伤指标能够更好地反映地震动和结构特性并降低结构分析结果的偏差，更准确地评估结构在动力荷载作用下的抗震性能[5]。研究表明，最大层间位移角θmax可以很好地反映框架结构的整体抗震性能[6]，而且中国抗震规范中采用地震动峰值加速度PGA表示不同烈度的设防地震动强度，并使用最大层间位移角θmax作为结构整体性能指标[8]。因此，选取PGA和θmax作为结构IDA分析的IM和DM指标。

1.4 损伤状态划分

根据文献[5]可列出RC框架结构破坏等级或性能水平与结构响应之间的关系，以RC框架结构在小、中、大震下的最大层间位移角限值[θmax]为依据，建立4个损伤状态并进行量化，如表1所示。

1.5 地震易损性分析

地震易损性表示不同强度地震作用下结构动力反应超过某损伤状态的条件概率，计算表达式为[6]

式中：结构反应超过某一损伤状态的概率为Pf，文献[7]研究认为，特定损伤状态下结构抗震能力概率函数C和结构反应概率函数D满足对数正态分布，根据文献[9]，式（1）可简化为

式中：λD和βD分别为结构反应概率函数D的对数平均值和对数标准差;λC和βC分别为结构抗震能力概率函数C的对数平均值和对数标准差;Φ（x）为标准正态分布累积概率函数;参照文献[10]的研究结论，当以PGA为变量时，β2D+β2C可取为0.5;C 为结构的损伤状态值;式（2）中的参数A、B按式（3）计算。

式中：A=ln α，B=β，系数A和B通过对结构IDA数据进行统计回归分析获得，α和β由式（4）获得[7]。

1.6 基于IDA的地震易损性分析基本步骤

1）建立合理的结构弹塑性分析模型;

2）依据相关规范要求选择符合要求的一系列地震动记录，选择合适的地震动强度指标IM和结构损伤指标DM，确定结构损伤状态;

3）确定地震动调幅原则和步长，得到一系列调幅后的地震动加速度时程记录。为了得到较完整的IDA曲线，且获得较精确的不同主震损伤状态所对应的IM值，结构IDA分析中IM增量步长取为0.01g;

4）计算结构在该调幅后地震动记录作用下的非线性动力时程响应，记录每次分析中的IM和DM值，得到IDA曲线簇;

5）统计IDA曲线簇的50%、84%、16%分位IDA曲线;

6）对IDA数据进行线性回归，建立以IM指标为自变量的结构概率地震需求模型;

7）计算不同地震动强度下结构达到损伤状态的失效概率，绘制地震易损性曲线。

2 模型概况

2.1 RC框架结构设计

根据中国现行建筑抗震设计规范[11]和混凝土结构设计规范[12]，使用PKPM软件对一栋6层钢筋混凝土框架结构进行抗震设计并计算截面配筋。结构主要设计参数如下：地震设防烈度为8度，设计基本地震加速度0.2g，场地类别Ⅱ类，设计地震分组第二组，场地特征周期0.40 s。结构底层层高4.2 m，其余层为3.6 m，6层结构总高22.2 m，抗震等级二级，建筑设防类别丙类。开间均为4 m，进深为6 m和2.7 m（走廊处），结构平面和立面图如图1所示。楼面永久荷载标准值取6 kN/m2，楼面可变荷载标准值取2 kN/m2，走廊可變荷载标准值取3.5 kN/m2，屋面永久荷载标准值取7 kN/m2，屋面可变荷载标准值取0.5 kN/m2，梁上线荷载标准值取8 kN/m2。梁、板、柱混凝土强度等级均为C30，梁、柱纵筋和箍筋均选取HRB400。RC抗震框架结构（RCF）构件截面尺寸及配筋详分别见表2和表3。

2.2 LVD减震框架结构设计

铅黏弹性阻尼器主要由约束钢板、黏弹性材料、剪切钢板、铅芯、连接端板等构成[3]，其内部构造如图2所示。根据建筑消能减震技术规程[13]，基于与RCF结构相同的设计参数，采用铅黏弹性阻尼器设计与RCF结构动力特性相近的铅黏弹性阻尼减震框架结构（LVDF）。依据文献[14]选取LVD的力学性能参数为：屈服荷载60 kN，初始刚度40 kN/mm，屈服位移1.5 mm。铅黏弹性阻尼器与主体结构连接方式示意图见图3，LVDF结构的梁柱截面见表1，梁柱配筋见表2。文中RCF结构和LVDF结构的反应谱最大层间位移角分别为1/559、1/564，两者较为接近。

2.3 OpenSees有限元模型

使用OpenSees软件[15]建立结构数值分析模型。铅黏弹性阻尼器采用考虑金属材料应变强化和包辛格效应的Steel02材料[16]进行模拟。如图4所示，通过与文献[3]中铅黏弹性阻尼器试件试验的滞回曲线对比可知，模拟得到的阻尼器最大阻尼力与试验结果相差仅2.47%，屈服前刚度和屈服后刚度基本吻合，说明该单元可以较好地模拟铅黏弹性阻尼器的力学特性。

根据文献[17]的建议，在OpenSees模型中使用刚性杆将水平荷载传递给阻尼器，阻尼器单元使用零长度单元模拟，支撑使用truss单元模拟，结构在地震动下的变形示意图见图5。

采用可以有效模拟RC构件塑性铰区强度和刚度退化的改进的IMK恢复力模型[18]模拟梁柱构件塑性铰区域的弹塑性力学行为，并将其置于Joint2D单元[19]的弹簧1～4，根据文献[20]提出的节点应力应变模型，Joint2D节点域的剪切弹簧5使用Hysteretic模型模拟，使用修正刚度的弹性梁柱单元[21]模拟RC梁柱构件中部未发生塑性变形的部分，使用零长度单元模拟首层柱柱脚的塑性铰，LVDF结构OpenSees模型详见图6。RCF结构建模方法与LVDF结构的主体框架结构相同。

3 地震易损性分析

3.1 IDA曲线

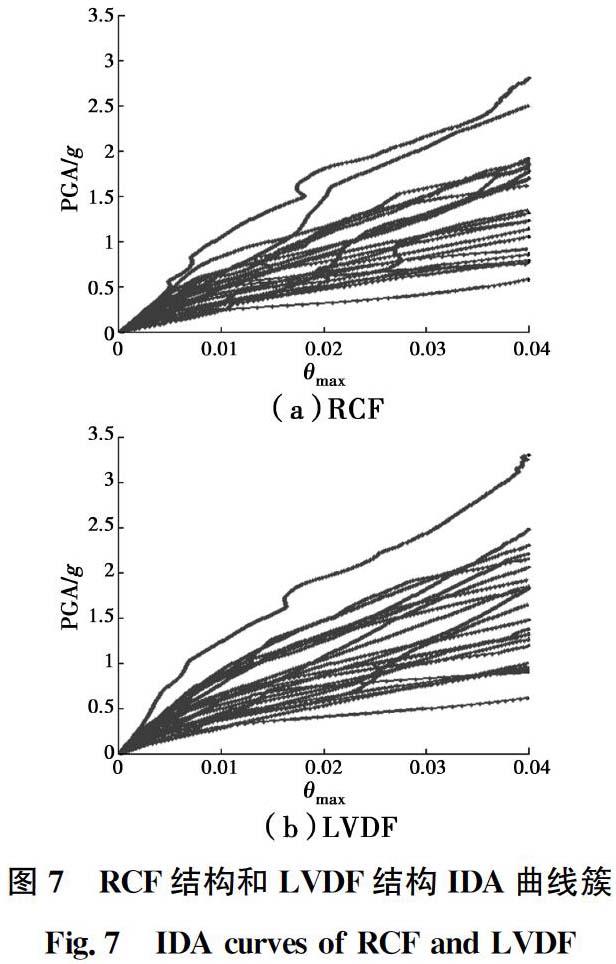
基于1.6节中的分析步骤，对结构分别输入调幅后的地震动记录进行弹塑性时程分析，得到IDA曲线簇如图7所示。由图7可知，相同最大层间位移下，LVDF结构的峰值地震动强度需求明显大于RCF结构，说明LVD对结构进行了有效的振动控制。

3.2 IDA分位曲线

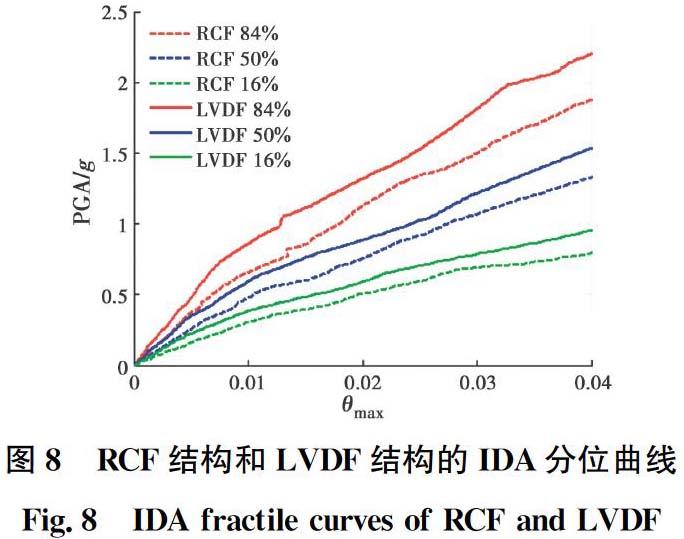
为准确评估结构的地震动响应特性，将IDA曲线汇总为可以表征IDA曲线簇平均水平和离散性的16%、50%和84%IDA分位曲线，如图8所示。由图8可知，LVDF结构的50%分位曲线比RCF结构低约3.7%，同一PGA下的LVDF结构的地震动响应小于RCF结构，说明LVD对结构进行了有效的振动控制。此外，RCF结构和LVDF结构的δIM中位数分别为0.348 5和0.338 6，说明LVDF结构的地震动响应离散性比RCF结构低约3%，使结构分析结果更加可靠。

3.3 概率地震需求模型

通过对数线性拟合建立结构反应DM与IM的结构地震需求概率函数关系式，如图9所示。

其中，RCF结构的概率地震需求模型为

LVDF结构的概率地震需求模型为

RCF结构和LVDF结构线性回归方程的相关系数R2分别为0.966 2和0.970 5，均大于0.95，表明线性回归方程与数据点之间的相关性较高，拟合效果较好，可以根据IDA结果得到的数据对RCF结构和LVDF结构进行地震易损性分析。此外，LVDF结构的R2大于RCF结构，这与前述IDA分位曲线的分析结果吻合，即LVD不仅可以降低整体结构的动力响应，还可以降低结构因地震动不确定性导致的动力响应的离散性。

3.4 地震易损性曲线

将式（5）和式（6）分别代入式（2），得到RCF结构和LVDF结构在各损伤状态的失效概率分别如式（7）和式（8）所示。

式中：C 为结构的损伤状态值，按照表1取值。根据失效概率公式即可绘制以PGA为横坐标的地震易损性曲线，如图10所示。由图10可知，各损伤状态下，LVDF结构在同一地震动强度下的超越概率均低于RCF结构，表明LVDF结构可以较好地降低结构在各损伤状态下的超越概率，提高结构的抗震性能。

3.5 结构破坏概率矩阵

根据图10的易损性曲线，可以预测量化8度（0.2g）设防地区的RCF结构和LVDF结构在小震、中震、大震和巨震[22]作用下发生不同损伤状态的破坏概率，形成结构破坏概率矩阵，如表4所示。

由表4可见，在8度小震作用下，RCF和LVDF均能保证结构的稳定性和安全性，达到损伤状态DS1的概率分别为38.62%和14.96%，超越其他损伤状态的概率基本为0。中震作用下，RCF结构有明显的损伤，达到损伤状态DS1和DS2的概率分别为96.02%和4.68%，而LVDF结构的超越概率为87.70%和1.16%，均小于RCF结构，说明LVDF结构的抗震性能优于RCF结构。大震作用下，RCF结构的损伤较为严重，损伤状态DS1的超越概率基本为1，DS2～DS4的超越概率分别为37.15%、4.32%和0.10%，均明显高于LVDF结构的20.67%、1.38%和0.02%，说明LVDF结构损伤得到较好的控制，具有较高的抗震性能。巨震作用下，虽然LVDF结构在DS1的超越概率与RCF结构相近，均接近100%，但LVDF在其他损伤状态下的超越概率均远小于RCF结构，说明LVDF结构即使在8度（0.2g）的极罕遇地震作用下也有较好的性能表现。综上所述，由图10和表4对比可知，在相同地震水平下，LVDF结构的破坏概率均小于RCF，平均降低约21%，即在结构震害评估过程中，LVD可以显著降低结構损伤，提高结构的抗震性能。

4 结论

基于相同设计参数分别设计并建立了动力特性相近的6层RCF结构和LVDF结构的有限元模型，对结构进行了增量动力分析和地震易损性分析，得到以下结论：

1）LVDF结构在同一地震动强度下的地震动响应比RCF结构低约4%，说明LVD可以有效降低结构地震动响应。

2）LVDF结构在不同地震动记录下地震动响应的离散性比RCF抗震结构低约3%，说明LVD可以降低因地震动特性差异导致的结构动力分析结果的离散性。

3）通过地震易损性分析结果可知，LVDF结构在不同损伤状态下的超越概率比RCF结构平均低约21%，说明LVD可以显著降低结构的损伤，提高结构的抗震性能。

参考文献：

[1] 潘毅， 陈侠辉， 赵俊贤， 等. 基于剪力比的黏弹性阻尼腋撑-RC框架结构设计方法[J]. 建筑结构学报， 2018， 39（Sup1）： 79-86.

PAN Y， CHEN X H， ZHAO J X， et al. Seismic design method of RC frame structure with knee brace of viscoelastic damper based on shear ratio [J]. Journal of Building Structures， 2018， 39（Sup1）： 79-86. （in Chinese）

[2] 房晓俊， 周云， 张超. 采用铅黏弹性连梁阻尼器的框架核心筒结构减震分析[J]. 土木工程学报， 2018， 51（Sup2）： 1-7， 13.

FANG X J， ZHOU Y， ZHANG C. Energy dissipation analysis of a frame-corewall structure equipped with lead-viscoelastic coupling beam dampers [J]. China Civil Engineering Journal， 2018， 51（Sup2）： 1-7， 13. （in Chinese）

[3] 石菲. 新型（铅）黏弹性阻尼器性能与应用研究 [D]. 广州： 广州大学， 2012.

SHI F. Performance and application research of （lead） viscoelastic damper [D]. Guangzhou： Guangzhou University， 2012. （in Chinese）

[4] 周云， 商城豪， 张超. 消能减震技术研究与应用进展[J]. 建筑结构， 2019， 49（19）： 33-48.

ZHOU Y， SHANG C H， ZHANG C. Progress in research and application of energy-dissipated technology [J]. Building Structure， 2019， 49（19）： 33-48. （in Chinese）

[5] 国巍， 曾晨， 潘毅， 等. 基于增量动力分析法的高层建筑-阻尼器系统地震易损性分析[J]. 土木与环境工程学报（中英文）， 2019， 41（4）： 59-68.

GUO W， ZENG C， PAN Y， et al. IDA based seismic fragility analysis of high-rise building-damper system [J]. Journal of Civil and Environmental Engineering， 2019， 41（4）： 59-68. （in Chinese）

[6] Quantification of building seismic performance and factors： FEMA-P695 [R]. Washington， DC： Federal Emergency Management Agency， 2009.

[7] VAMVATSIKOS D， CORNELL C A. Incremental dynamic analysis [J]. Earthquake Engineering & Structural Dynamics， 2002， 31（3）： 491-514.

[8] 潘毅， 包韵雷， 国巍， 等. 摆式电涡流TMD-钢框架结构的耦合计算方法与减震分析[J]. 土木与环境工程学报（中英文）， 2020， 42（4）： 84-93.

PAN Y， BAO Y L， GUO W， et al. Coupling calculation method and seismic analysis of pendulum eddy current TMD-steel frame structures [J]. Journal of Civil and Environmental Engineering， 2020， 42（4）： 84-93. （in Chinese）

[9] HUANG W Y， ZHANG C， SHI F， et al. Study on seismic performance and energy demand of RC frame constructed with lead viscoelastic damper under strong earthquake [C]// The 9th Asia-Pacific Young Researchers and Graduates Symposium， Shanghai， China， 2019.

[10] Earthquake loss estimation methodology： users manual： FEMA HUZUS99 [R]. Washington， DC： Federal Emergency Management Agency， 1999.

[11] 建筑抗震设计规范： GB 50011—2010 [S]. 北京： 中国建筑工业出版社， 2010.

Code for seismic design of buildings： GB 50011-2010 [S]. Beijing： China Architecture & Building Press， 2010. （in Chinese）

[12] 混凝土结构设计规范： GB 50010—2010 [S]. 北京： 中國建筑工业出版社， 2011.

Code for design of concrete structures： GB 50010-2010 [S]. Beijing： China Architecture & Building Press， 2011. （in Chinese）

[13] 建筑消能减震技术规程： JGJ 297—2013 [S]. 北京： 建筑工业出版社， 2013.

Technical specification for seismic energy dissipation of buildings： JGJ 297-2013 [S]. Beijing： China Architecture & Building Press， 2013. （in Chinese）

[14] 房晓俊. 功能自恢复连梁抗震性能研究[D]. 广州： 广州大学， 2018.

FANG X J. Study on seismic performance of self-resilient coupling beam [D]. Guangzhou： Guangzhou University， 2018. （in Chinese）

[15] OpenSees. Open system for earthquake engineering simulation[R]. Pacific Earthquake Engineering Research Center， University of California： Berkeley， CA， 2007.

[16] FILIPPOU F C， POPOV E G， BERTERO V V. Effects of bond deterioration on hysteretic behavior of reinforced concrete joints [R]. Berkeley： Earthquake Engineering Research Center， 1983.

[17] MOHAMMADI R K， NASRI A， GHAFFARY A. TADAS dampers in very large deformations [J]. International Journal of Steel Structures， 2017， 17（2）： 515-524.

[18] IBARRA L F， MEDINA R A， KRAWINKLER H. Hysteretic models that incorporate strength and stiffness deterioration [J]. Earthquake Engineering & Structural Dynamics， 2005， 34（12）： 1489-1511.

[19] CELIK O C， ELLINGWOOD B R. Modeling beam-column joints in fragility assessment of gravity load designed reinforced concrete frames [J]. Journal of Earthquake Engineering， 2008， 12（3）： 357-381.

[20] TERAOKA M， FUJII S. Seismic damage and performance evaluation or R/C beam-column joints [C]// The Second US-Japan Workshop on Performance-Based Engineering for Reinforced Concrete Building Structures， Hokkaido， Japan， 2000， 379-390.

[21] IBARRA L F， KRAWINKLER H. Global collapse of frame structures under seismic excitations [R]. The John A. Blume Earthquake Engineering Center， Stanford University， Stanford， CA， 2005.

[22] 中国地震动参数区划图： GB 18306—2015 [S]. 北京： 中國标准出版社， 2016.

Seismic ground motion parameters zonation map of China： GB 18306-2015 [S]. Beijing： Standards Press of China， 2016. （in Chinese）

（编辑 胡玲）