基于完全活性空间自洽场的杂化多组态密度泛函方法λ-DFCAS

应富鸣，计辰儒，苏培峰，吴 玮

（厦门大学固体表面物理化学国家重点实验室,福建省理论与计算化学重点实验室,化学化工学院,厦门361005）

1 Introduction

Correlation energy plays an important role in computational quantum chemistry to provide accurate enough numerical results of physical and chemical properties，such as bond dissociation energy（BDE），reaction barrier and reaction energy.Correlation energy can be roughly classified into static and dynamic correlations.Static correlation comes from the near-degenerate configuration states，which cannot be described properly by a single-determinant wave function，while dynamic correlation is due to the excitations of the electrons from occupied orbitals to virtual ones.Complete active space self-consistent field（CASSCF）is a typical multi-configurational method and is widely used to get static correlation［1，2］.Post-CASSCF methods were developed to make dynamic correlation included，such as multi-reference second-order perturbation theory（MRPT2）［3—6］，multi-reference configuration interaction（MRCI）［5，7］，and multi-reference coupledcluster（MRCC）etc.However，the computational cost goes up rapidly with the active space of molecule，which limits the applications of these methods.

On the contrast，Kohn-Sham density functional theory（KS-DFT）［8—11］becomes one of the most widely spread methods for its low cost and satisfactory accuracy.KS-DFT gets electronic density from a fictious singledeterminant wave function which provides the same densityρas the real system，and the correlation energy is included in exchange-correlation functionalEXC［ρ］.However，KS-DFT suffers from a difficulty of treating molecules with strong multireference character，due to the use of single-determinant wave function.To get rid of this difficulty，the idea of combining multireference wave function with density functional theory（DFT）seems a practical solution.As such，there have been various multireference based DFT methods，namely multireference density functional theory（MRDFT）［12—25］，proposed since 1990s，where most of them combine CASSCF/multiconfigurational self-consistent field（MCSCF）wave functions and KS-DFT functionals.One of the problems that should be solved carefully in MRDFT is double counting error（DCE），as the static and dynamic correlations cannot be separated strictly.Range separation treatment that divides the two-body operator in Hamiltonian into two terms can remedy the DCE problem，where the long-range term is involved in the wave function method，while the short-range term is treated with density functional theory.Alternatively，a simpler scheme，called multiconfigurational one-parameter hybrid（MC1H）approximation，is proposed by Toulouse and coworkers［26］，which decomposes the electron-electron interactions linearly with one hybrid parameterλto get rid of the DCE problem.

As one of the modern chemical bonding theories，valence bond（VB）theory［27—29］has provided an intuitive tool for exploring the nature of chemical bonding.Though computational VB methods are much less developed at theabinitiolevel than molecular orbital theory，VB theory has been enjoying a renaissance since 1980s［27—47］.In VB theory，a many-electron wave function is expressed as a linear combination of VB functions，which correspond to“classical”VB structures，and are further written in terms of atomic orbital based Slater determinants.That is to say，VB methods are inborn multireference wave function methods.Various schemes of combining VB method with KS-DFT have been attempted，including VBDFT（s）［48］，VB-DFT［49］，and DFVB［50—53］.Among them，λ-DFVB［52］is a recently presented DCE-free hybrid method that combines VB theory with DFT by utilizing the MC1H approximation.However，different from the MC1H approximation［26］，in which parameterλis suggested to a fixed value of 0.25，the value ofλis variable，according to the extent of multireference character of molecule.Primary test results show that the performance ofλ-DFVB is at par with complete active space second perturbation theory（CASPT2）.Lately，a revisitedλ-DFVB method［53］was published by defining parameterλas a function of natural orbital occupation numbers，instead of the free valence of molecule used in the originalλ-DFVB method.

Althoughλ-DFVB provides a novel VB method that covers both static and dynamic correlations，the VB-based MRDFT method still faces some practical difficulties.First，abinitioVB methods are still computational expensive，due to the use of nonorthogonal atomic orbitals，compared with CASSCF，particularly for full VB structure calculations.Secondly，abinitioVB programs are still scarce in computational quantum chemistry community，limiting the application ofλ-DFVB.On the contrast，as one of the widely used molecular orbital（MO）-based multireference wave function methods，CASSCF has been implemented in most of quantum chemistry programs，and algorithms used in CASSCF are fully optimized.Therefore，it is worthwhile to apply the strategy ofλ-DFVB to CASSCF.

The aim of the paper is to present a novel MO-based MRDFT method by using the same scheme as inλ-DFVB，namedλ-DFCAS.That is to say，the MC1H approximation is used，but the parameter value is variable as multireference character of molecule.Furthermore，one more term，which accounts for the correlation of a single determinant，is added to the MC1H energy expression［26］.The performance ofλ-DFCAS method is validated by computing various physical and chemical properties，including equilibrium bond length，vibrational frequencies，bond dissociation energies，reaction barriers and reaction energies.

2 Theory and Methodology

The CASSCF wave functionΨof aN-electron system is expressed as a linear combination of molecular orbital based Slater determinants｛DK｝，as

where both determinant coefficients｛CK｝and MOs are optimized simultaneously in SCF procedure.

In the MC1H approximation proposed by Toulouse and coworkers［26］，the MRDFT energyEMC1His expressed by

Inλ-DFVB，valence bond self-consistent field（VBSCF）［30，31］wave function is applied to Eq.（2）as the many-electronic wave functionΨVBSCF，and thus the total energyEλ-DFVBis expressed as

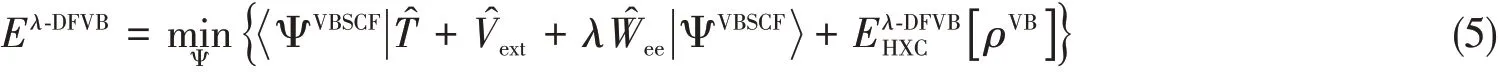
whereρVBis the corresponding density ofΨVBSCF.The Hartree-exchange-correlation density functionalinλ-DFVB is different from eq.（3），defined as

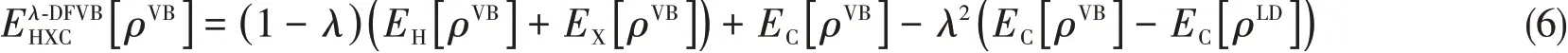
The difference between Eqs.（2）and（6）is thatEC［ρLD］is added in Eq.（6），which is the correlation functional of a single determinant in VBSCF wave function that shares the largest coefficient，thus called leading term（LD）.Furthermore，parameterλis defined as a function of free valence of molecule.

The free valenceFAon atomAis defined as

whereVAis the total valence on atomA

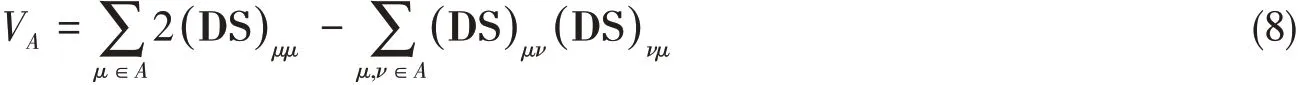
andOABis the Mayer’s bond order［54］between atomsAandBexpressed as

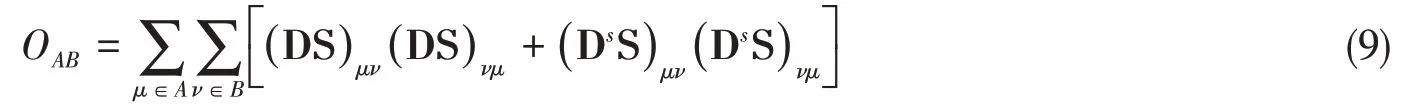
In Eqs.（8）and（9），S is the overlap matrix of basis functions，D=Pα+Pβis the total density matrix and Ds=Pα-Pβis the spin-polarized density matrix，where Pαand Pβare density matrices ofαandβelectrons respectively，and indicesμandνrefre to basis functions.The parameterλis defined as

As can been seen from Eq.（10），at the dissociation limit，FA=VA，and thusλ=1，resulting in the range of 0—1 of parameterλ.

Applying the scheme ofλ-DFVB to CASSCF wave function，one can design a new MRDFT method，namedλ-DFCAS.In theλ-DFCAS method，CASSCF wave functionΨCASSCFis used to compute the contribution of wave function theory to the total energy and determine the electronic density for functional.Thus，

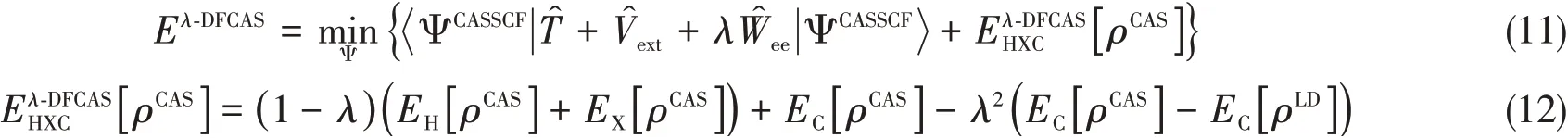
whereEC［ρLD］is theECenergy of the leading determinant in CASSCF wave function.

In theλ-DFVB method，the VB wave function is optimized by minimizing theλ-DFVB energy with Eq.（5）.Numerical test shows that the minimization through SCF does not affect the final result dramatically.Thus，to reduce the computational cost，instead of minimizing theλ-DFCAS energy with Eq.（11），theλ-DFCAS energy is computed directly with the CASSCF wave function，by

Therefore，theλ-DFCAS method just makes an energy correction based on CASSCF wave function，and the computational cost is the same as that of CASSCF calculation.

The computational procedure ofλ-DFCAS is as follows：（1）A CASSCF calculation is carried out to obtain the wave functionΨCASSCF，energyECASSCF，densityρCAS，and individual energy terms，T，Vext，WeeandEH；（2）evaluate theλvalue by Eqs.（7）—（10）；（3）determine the leading determinant in CASSCF wave function，then compute its densityρLD；（4）obtainEX［ρCAS］，EC［ρCAS］andEC［ρLD］from KS-DFT rountines with densitiesρCASandρLD；are computed by Eqs.（12）and（13）.

3 Computational Details

Theλ-DFCAS method has been implemented in a modified GAMESS program［55，56］.All CASSCF，CASPT2，λ-DFCAS and KS-DFT calculations were carried out by GAMESS.Valence bond calculations including VBSCF，dc-DFVB，hc-DFVB andλ-DFVB ones were computed by Xiamen Valence Bond program［57─60］.

Test calculations included thermodynamic properties of diatomic molecules of H2，HF，C2，N2and F2，the barriers of the seven reactions：（Ⅰ）NH3+CH3Cl→［NH3CH3］++Cl-；（Ⅱ）synchronous Diels-Alder reaction with cyclic transition state，C4H6+C2H4→C6H10；（Ⅲ）H+N2O→OH+N2；（Ⅳ）OH+N2→H+N2O；（Ⅴ）Cl-+CH3Cl→CH3Cl+Cl-；（Ⅵ）isomerization of HCN to HNC；（Ⅶ）isomerization of HNC to HCN.

Various methods，including VBSCF，dc-DFVB，hc-DFVB，λ-DFVB，CASSCF，CASPT2，λ-DFCAS.KS-DFT functionals PBE and B3LYP，were employed.For DFVB andλ-DFCAS，the exchange functional B88 and the correlation functional LYP were used.The basis set cc-pVTZ was used for thermodynamic properties，while 6-31G*and MG3S were employed for chemical reactions.For comparison，full configuration interaction（FCI）results were included in the potential energy curves.The FCI curve of H2was obtained by MRCISD with cc-pVTZ basis set，while others were obtained from literature［12］.

4 Results and Discussion

4.1 Time Cost ofλ-DFCAS

Table 1 lists the time costs by CASSCF，CASPT2 andλ-DFCAS for diatomic molecules F2，C2，and several transition states of chemical reactions.In general，the cost ofλ-DFCAS is close to CASSCF，smaller than CASPT2.For molecules with small active spaces such as F2and C2，λ-DFCAS takes similar time as CASPT2，while for the large active space，λ-DFCAS is faster than CASPT2.Most of the time consumed byλ-DFCAS is taken in the CASSCF procedure sinceλ-DFCAS energy is obtained directly from CASSCF wave function.

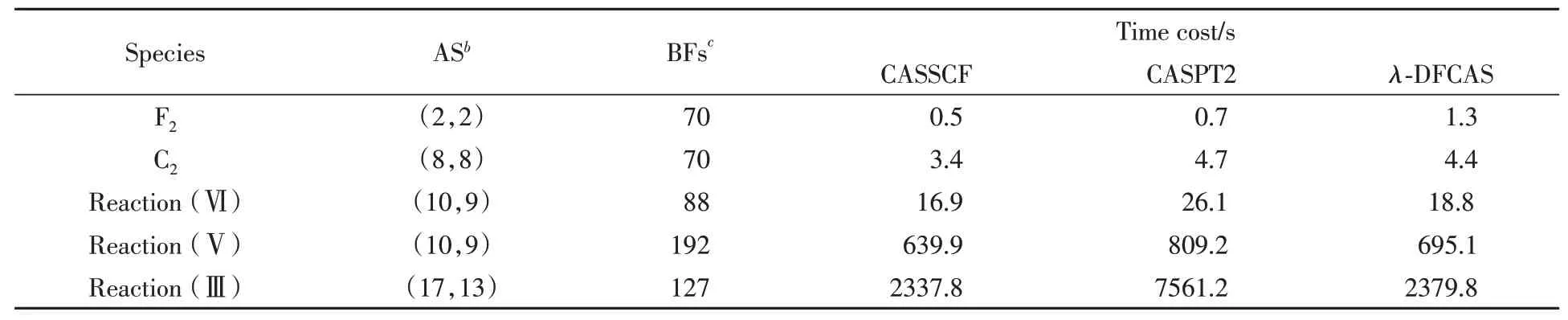
Table 1 Time costs for F2,C2 and TSs of reactions(Ⅲ),(Ⅴ)and(Ⅵ)by CASSCF,CASPT2 andλ-DFCAS a

4.2 Potential Energy Curves and Thermodynamic Properties of Diatomic Molecules

Figs.1（A）—（E）display the potential energy curves of diatomic molecules H2，F2，HF，C2and N2，respectively.For the convenience of comparison，the vertical axis is the relative energy（ΔE）compared with the energy at dissociation limit for all methods，and the subplot shows the data around the equilibrium bond distances.CASSCF shows energies far from FCI values and hence provides the poor BDEs due to the lack of dynamic correlation.In general，theλ-DFCAS curves are close to FCI，DFVB and CASPT2 at their short distances.When the bond dissociation proceeds，λ-DFCAS curves go to the dissociation limit faster than FCI.This is especially clear in F2and N2，as shown in Figs.1（B）and（E）.

The optimized equilibrium distances of diatomic molecules are listed in Table 2，where the results of the deviations to experimental data［61］are shown，the same below.It can be found thatλ-DFCAS is capable of predicting the excellent distances compared to high level computational methods.The mean unsigned error（MUE）for the deviations ofλ-DFCAS results to experimental data，0.0012 nm，is smaller than those of VBSCF and CASSCF，and close to those ofλ-DFVB，B3LYP and CASPT2.For instance，the deviation ofλ-DFCAS for C2is only 0.0004 nm，comparable to the value ofλ-DFVB（-0.0001 nm）.

Table 3 lists vibrational frequencies of diatomic molecules by various methods with reference data［50─52，61］.The MUE ofλ-DFCAS is 79 cm-1，which is the smallest among all the results.For example，for F2，the deviation ofλ-DFCAS is 109 cm-1，close to the value of B3LYP（139 cm-1），and smaller than that of CASSCF（-219 cm-1）.For C2and N2，the deviations ofλ-DFCAS are-45 and-37 cm-1，almost the same as those of CASPT2，43 and-39 cm-1，respectively.

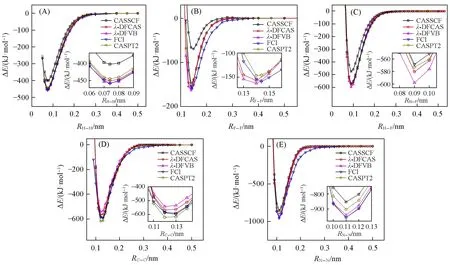
Fig.1 Potential energy curves of H2(A),F2(B),HF(C),C2(D)and N2(E)

Table 2 Equilibrium distances of diatomic molecules*

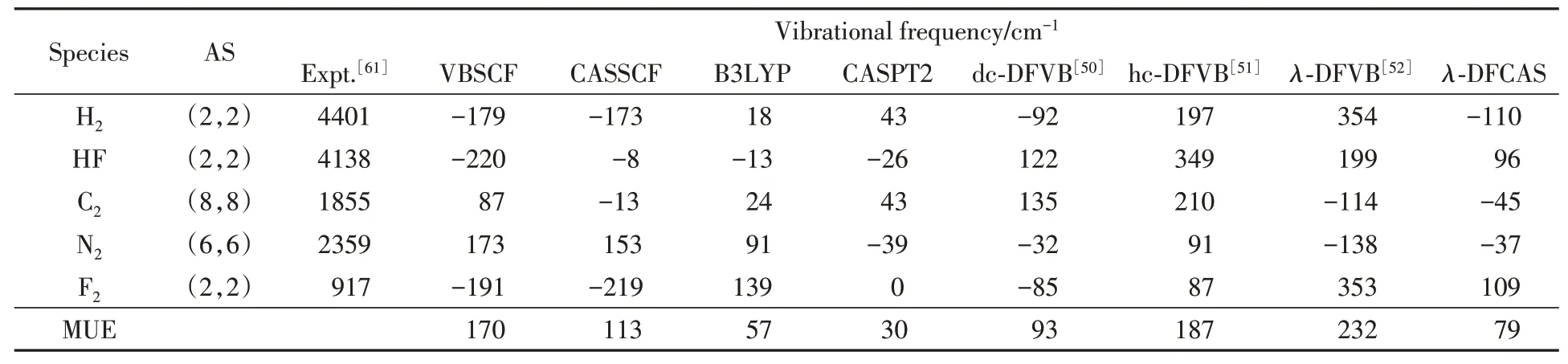
Table 3 Vibrational frequencies of diatomic molecules*

Table 4 shows the bond dissociation energies（BDEs）of diatomic molecules with reference data［50─52，61］.The results ofλ-DFCAS are as accurate as those ofλ-DFVB and CASPT2.In details，the MUE ofλ-DFCAS，17.2 kJ/mol，is close to that of CASPT2，20.1 kJ/mol，and better than that of B3LYP，24.7 kJ/mol.For example，the deviation ofλ-DFCAS for N2is-5.9 kJ/mol，which is the smallest among all the methods.

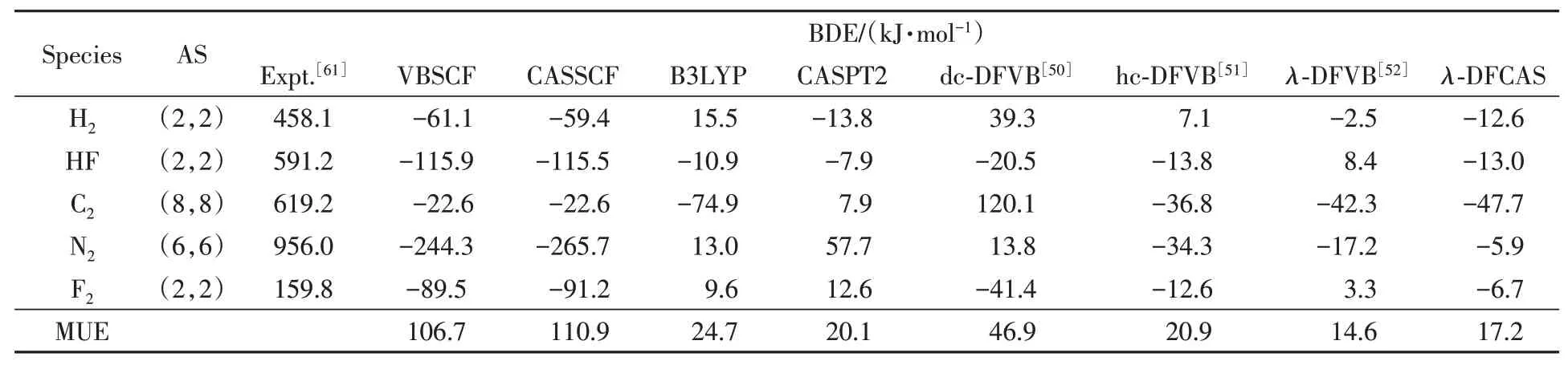
Table 4 BDEs of diatomic molecules*

4.3 Chemical Reactions

The reaction barriers by various methods with reference data［62─64］are shown in Table 5.In general，the MUE ofλ-DFCAS is 11.7 kJ/mol，which is close to that of CASPT2，9.6 kJ/mol，and better than those of KS-DFT.In details，the deviation ofλ-DFCAS is 4.2 kJ/mol for reaction（Ⅴ），which is better than CASPT2.For reaction（Ⅳ），the deviation ofλ-DFCAS is the same as that of CASPT2，better than those of PBE，B3LYP and MC-PDFT（-44.8 kJ/mol［62］）.

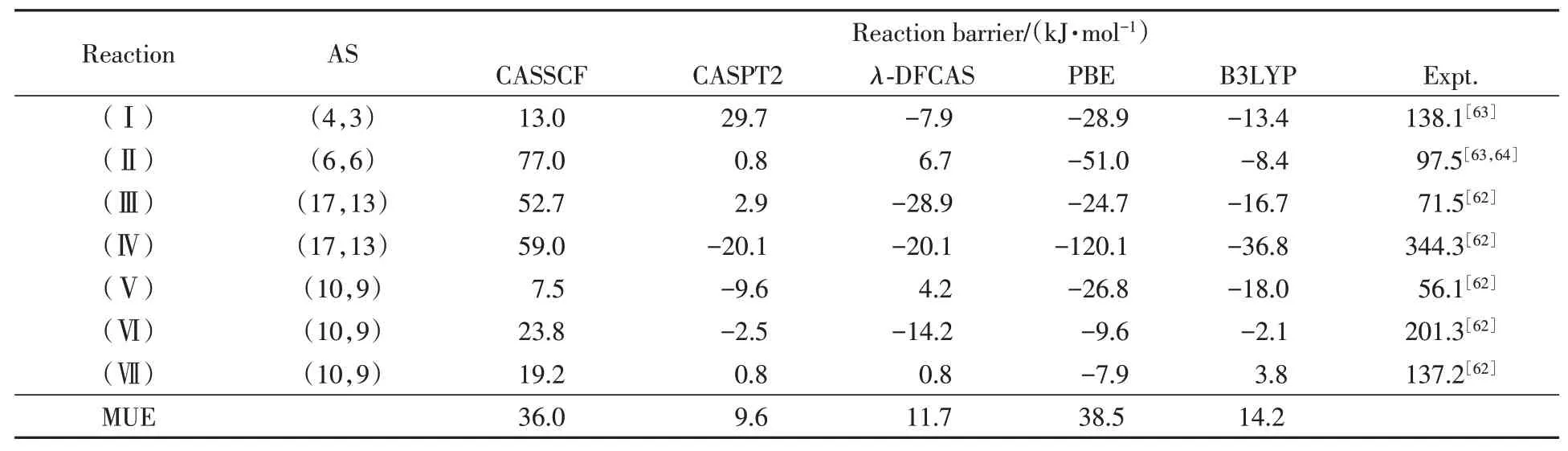
Table 5 Computational barriers of chemical reactions*

Table 6 lists the computational chemical energies for reactions（Ⅰ），（Ⅲ）and（Ⅵ）.In general，the performance ofλ-DFCAS is quite good.For instance，the deviation ofλ-DFCAS for reaction（Ⅲ）is 8.8 kJ/mol，better than CASPT2 and MC-PDFT shown in literature［62］.

Table 6 Chemical reaction energies by various methods*

5 Conclusions

The hybrid density functional complete active space self-consistent field method，λ-DFCAS，is proposed，which applies the same strategy asλ-DFVB.λ-DFCAS remedies the double-counting error of electron correlation by using a variable parameterλto decompose the electron-electron interactions into the wave function part and density functional part.The parameterλvaries from 0 to 1，measuring the multiconfigurational character of the system.Various examples，including potential energy curves，equilibrium distances，vibrational frequencies，bond dissociation energies，chemical reaction barriers，and chemical reaction energies are used to test the performance ofλ-DFCAS.In general，the accuracy ofλ-DFCAS is close toλ-DFVB and CASPT2，while its computational cost is almost the same as CASSCF.

This paper is supported by the National Natural Science Foundation of China（Nos.21733008，21973077）.