一种介质集成悬置线结构的介电常数测量装置
2021-07-11马奎刘长军陈倩
马奎,刘长军,陈倩
四川大学 电子信息学院,四川 成都 610064
作为表征介质电极化性能的重要电磁学参量,复介电常数一直是国内外学者研究的一个重要方向[1-2]。在工程应用中,准确、高精度、快速实时地对介电常数进行测量具有重要意义[3]。目前通常通过间接测量物体介电常数改变引起的测量系统其他参数,如传播常数、品质因数、频率偏移和相位衰减等[4-5]变化来达到测量目的。其中基于平面传输结构的谐振法测量装置[6-7]结构简洁,应用广泛。文献[8]提到一种利用微带线谐振法测量液体S 波段复介电常数的方法,使用了牛顿迭代法对数据进行反演,介电常数实部和虚部相对误差分别为4.4%和8.6%。文献[9]提出一种利用矩形基片集成波导谐振腔测量液体复介电常数的方法,使用人工神经网络进行反演,实部和虚部相对误差分别为5%和7%。文献[10]提出了一种使用基片集成波导构成的双频测量装置,通过2 个级联的谐振器,能够在双频点进行测量。
谐振法测量介电常数时,装置的衰减情况通常是制约测量性能和精度的最重要因素。在面对高损耗待测介质时,谐振状态往往不易保持。本文提出了一种使用介质集成悬置线(SISL)的复介电常数测量装置,通过使用封闭结构形成谐振腔,减少了损耗,提高了品质因数和介电常数测量的精度及适用范围。待测样品通过谐振腔表面的缝隙间接影响空腔内谐振的频率和Q值,使用人工神经网络对测量数据进行求解。
1 测量装置的原理分析及设计
传统的微带悬置线由于其出色的传输性能和功率容量在滤波器、功分器[11-12]等器件设计上具有很好的适用性,然而其体积结构笨重、难以与其他电路集成的劣势同样突出。2007 年Ma 等[13]提出了一种新的介质集成悬置线改良结构,有效地避免了悬置线尺寸上的劣势,同时保留了其良好的传输性能,并具有很高的集成度。目前基于这种新型结构的微波电路得到了国内外的广泛关注[14-15]。典型的SISL 物理结构如图1 所示,由5 层印刷电路板及电路板上下印制铜板(金属层1—金属层10)构成,四周采用金属过孔作电壁。电路设计主要在第3 层的金属层5 和金属层6 这2 个表面上,这使得SISL 与其他常见的微带以及共面波导(coplanar waveguide,CPW)等平面电路一样,易于集成。针对这种新型传输线的性能优势,使用有限元数值计算方法对几种主要传输线的衰减情况进行了仿真,图2 为多种传输线在特征阻抗为50 Ω 时的衰减常数对比。由图2 可以看到在同等条件下,悬置线的衰减常数比金属波导略高,这一定程度上证明了SISL 结构具有优秀的传输性能。
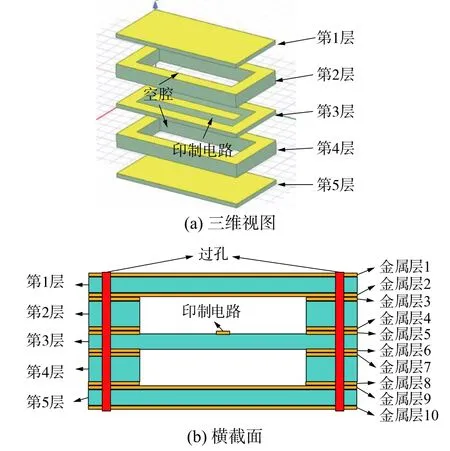
图1 介质集成悬置线结构
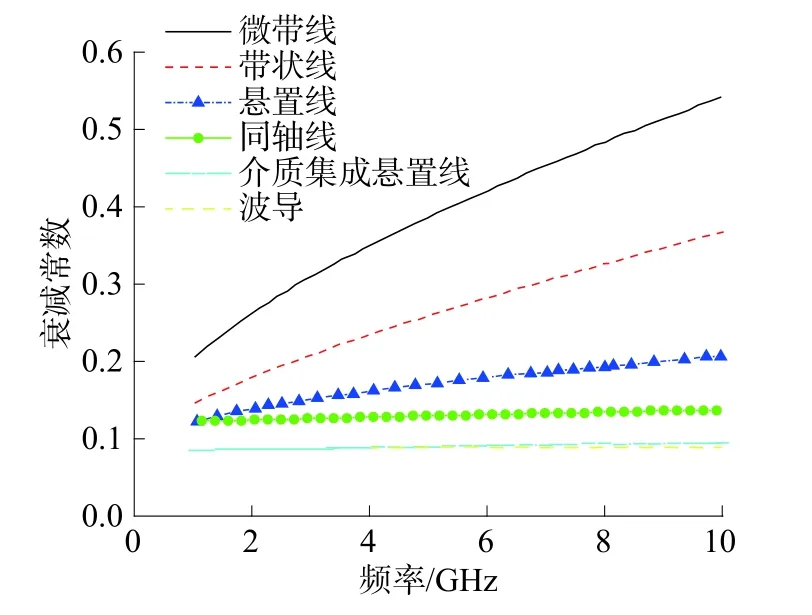
图2 SISL 与多种传输线衰减对比
本文基于谐振法测介电常数的原理,使用SISL 结构,根据其结构特点设计了一款工作于5.8 GHz 的悬置线谐振器。设计结构共5 层,第1、3、5 层介质板为1 mm 厚度的F4B 材质,相对介电常数为2.2;第2、4 层为中间正方形镂空的FR-4 介质板,厚度为1.6 mm,相对介电常数为4.3;中间镂空区域长度为25 mm,宽度为11 mm;谐振金属导带位于金属层5,宽度为3 mm;四周金属通孔的直径为1 mm,彼此间隔2 mm。
当谐振器工作在谐振状态时,其电磁场分布于内部空腔和第3 层介质板中,与外界几乎隔离。此时电磁场存在的空间可以看作被等效介电常数为εe的均匀介质填充,容易得出εe的大小介于空气和第3 层介质板介电常数之间,且与介质板所占空间的比例直接相关。结构整体厚度不变的情况下,介质板的厚度越薄,εe的值越接近1,电磁波在内部的介质损耗越小。此时SISL 的等效介电常数和特征阻抗计算可以视作与传统悬置线相同。根据导带宽度与空腔尺寸比值的不同,大致可以分为宽导带和窄导带2 种情况。文献[16]给出了不同尺寸和介电常数环境下的多种计算方法,可以方便地计算任意情况下的εe和特征阻抗。
本设计中谐振金属导带可以看作是四周增加金属屏蔽罩的微带线,其长度遵循终端开路的半波长微带谐振器设计方法,长度l为
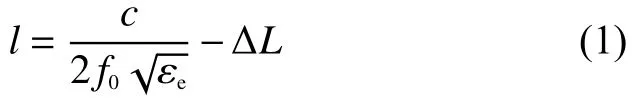
式中:c为真空中光速,f0为谐振频率,ΔL为导带与边框和地之间的耦合效应造成的长度缩减。
谐振器的Q值与电磁场的衰减有关,本结构中的衰减来源包括内部空腔上下金属壁上的导体损耗、金属化通孔之间的辐射损耗、谐振金属导带上的导体损耗和空腔内的介质损耗。其中辐射损耗极小,可以忽略。结构的空载品质因数为
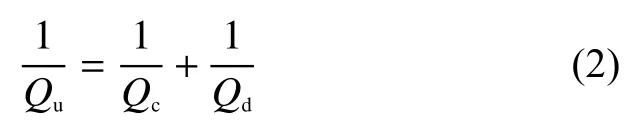
式中Qu、Qc和Qd分别代表空载品质因数、无介质损耗和无导体损耗时的品质因数值。
Qd与损耗正切的关系有
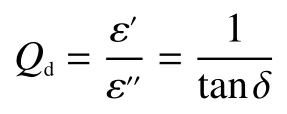
实际测量时,在谐振器第1 层介质层上下金属层对应位置开缝,用于引入不同待测样品对空腔内电磁场的微扰,从而改变谐振器的谐振频率和品质因数[17],可以认为只有介质损耗情况会发生变化。此时,待测样品的引入可以看作改变了空腔中等效介电常数εe。这将使空腔内部的介质损耗情况发生变化,从而改变式(2)中Qd和Qu的值;同时根据式(1),εe的变化将使谐振频率变化。
图3 为所设计耦合器各层介质板的结构。第1 层介质板上下对应位置开有细缝,缝隙宽度为2.5 mm,长度为17 mm,位于空腔上方正中央。设计的SISL 谐振器通过一个微带线—带状线—悬置线的3 级过渡结构与外部50 Ω 的同轴馈电接口连接,谐振金属导带则通过缝隙耦合的方式进行激励。微带线、带状线和悬置线均位于第3 层介质板的上表面,即金属层5。金属层6 作为微带线和带状线的公共地,谐振金属导带也位于这一层。为使每个部分连接处不出现反射,各个部分的设计阻抗均应为50 Ω,故微带线宽W1为3 mm,带状线宽度W2为1.4 mm;微带线Lmicro和带状线Lstrip长度分别为6 mm 和4.5 mm;同时微带线与地间隙S1为2.5 mm,带状线与地间隙S2为1.2 mm。悬置线宽度与缝隙耦合系数有关,根据计算机仿真结果选取宽度W3为1.1 mm,长度Lup为1.2 mm。由式(1)和仿真优化,选取谐振金属导带尺寸为21 mm×3 mm。
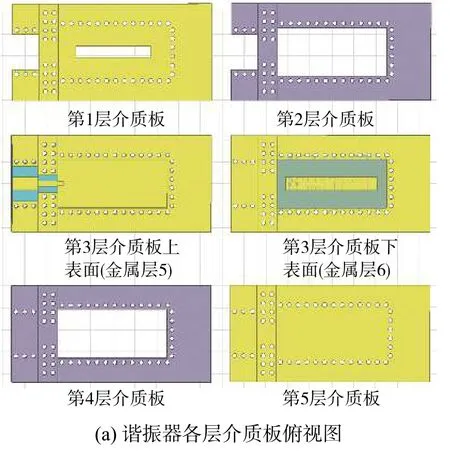
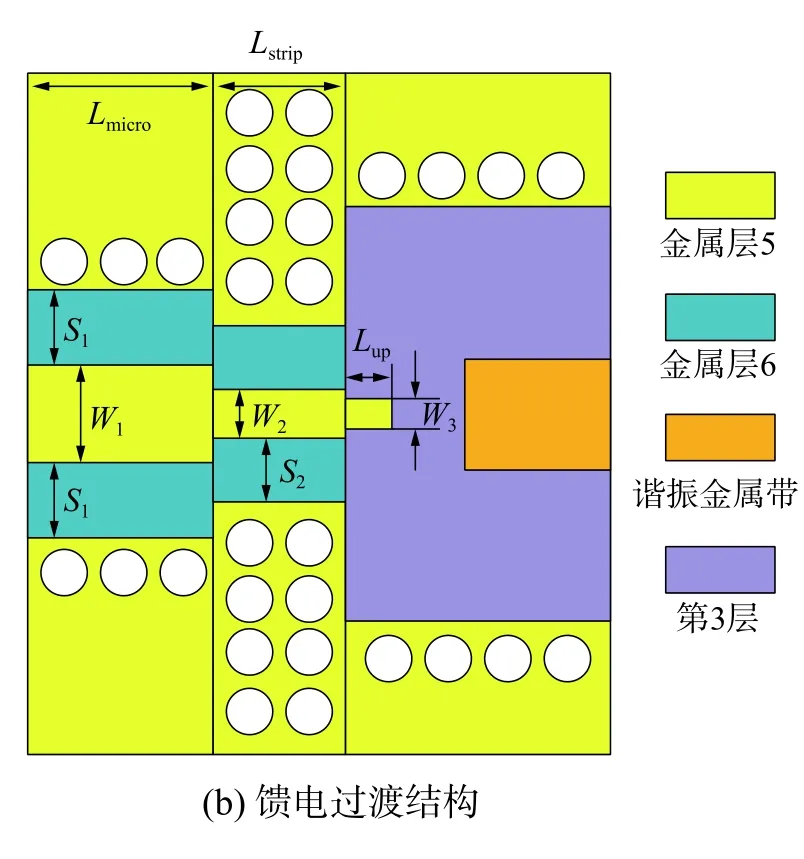
图3 介质板结构
2 测量与反演结果
实验中,使用了去离子水-乙醇混合溶液作为待测样品,使用Agilent N5230A 矢量网络分析仪连接测量探头进行测量。为固定加载的待测样品,避免其接触到缝隙外的其他介质而造成测量结果不准的问题,使用3D 打印机制作了一个矩形方框粘贴在表面缝隙上方,以保证待测物固定于电场最强处,图4 为测量探头实物。根据理论分析和实验证明,附加矩形方框对结构的谐振状态几乎没有影响。

图4 测量探头实物
表1 为实测空气中探测器和经校准后仿真的谐振频率和Q值对比。由表1 可以看到,仿真和实测的频率结果基本一致。
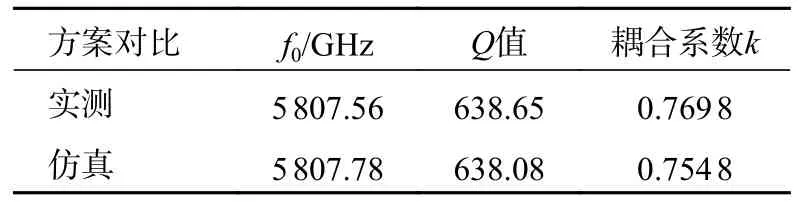
表1 实测和仿真数据对比。
乙醇-水混合溶液具有介电常数变化范围大、无毒害和方便配置等特点。在30 ℃左右的室温下,依照乙醇体积分数(0~100%)等比例增长和等溶剂量增长(0∶50,10∶50,20∶50,30∶50,40∶50,50∶50,50∶40,50∶30,50∶20,50∶10,50∶0)的方式,配置了11 份不同体积分数的乙醇-水混合溶液。依次将配置好的溶液加入探测器矩形方框中,使用矢网在5.75~5.85 GHz 对探测器S参数进行测量,并记录稳定读数用以计算谐振频率和Q值。探头2 次测量不同乙醇体积分数对应的频率偏移量和Q值变化如图5 所示。由图5 可以看出,随着体积分数的提高,频率偏移量不断下降,而品质因数不断上升。2 次测量的结果前后基本一致。

图5 测量结果随乙醇体积分数增加的变化曲线
由于待测物介电常数ε与腔体的谐振频率和品质因数的关系很难直接求解,本文利用BP 神经网络反演系统作为数据关系重构工具。人工神经网络模拟生物大脑的作用机理,使用神经元模型作为其基本组成单位,多个神经元使用不同的权值相互连接,能够使整个系统对复杂问题做出精确的判断和分析。神经网络的训练过程实际上就是这些权值的求解过程。
使用神经网络反演需要训练和计算2 个阶段,针对本文的具体情况,按照以下步骤进行。
1)对加载若干组不同复介电常数测量物的模型进行仿真计算,从计算出的S参数中得到相应的谐振频率和Q值。
2)将频率相对空气加载时的偏移量和Q值作为神经网络的输入层数据,介电常数实部和虚部作为输出层数据,开始训练并根据情况不断调整网络的神经元个数和学习率,保存收敛后的神经网络。
3)使用测量得到的相对频率和Q值输入到训练好的网络中,即可得到待测样品的介电常数。
按照上述步骤,绘制了神经网络反演得到的介电常数实部和虚部随乙醇体积分数的走势,以及与理论值的对比[18],如图6 所示。测量后的实部平均误差为3.75%,虚部平均误差为1.29%,与理论值吻合良好,结果准确。
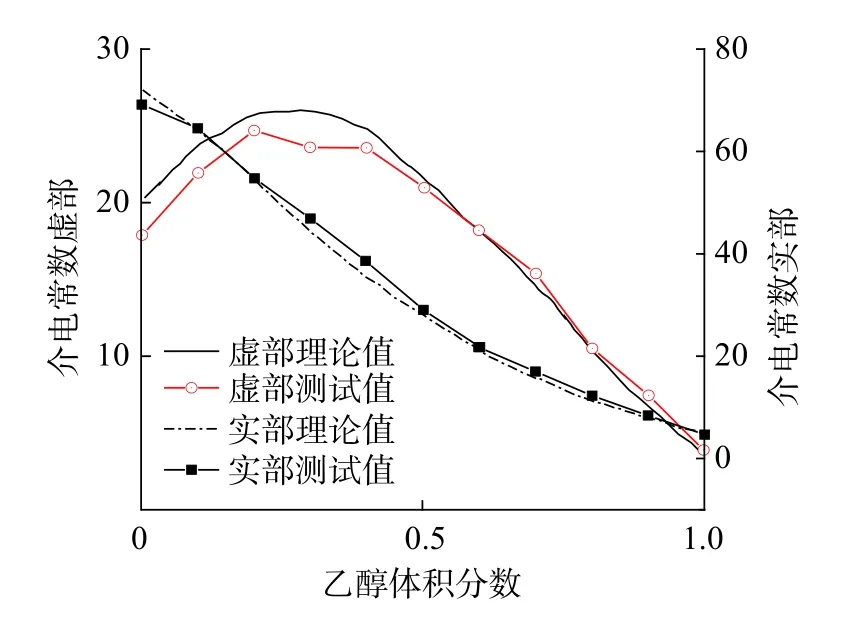
图6 混合溶液等效复介电常数实测和理论值
3 结论
1)本文设计了一种工作于5.8 GHz 的高Q值新型介电常数测量结构,经过加工测量,计算机仿真和实测结果吻合良好。
2)装置在对乙醇-水二元混合溶液的精确实验中表现良好,测量结果与理论平均误差实部为3.75%,虚部为1.29%,特别是在对高损耗介质的测量上,其谐振现象依旧十分明显,为测量提供了高准确度依据。
3)通过使用人工神经网络对测量数据进行预测,为介电常数的计算提供了很大的便捷性。
本装置相比于其他同类设计,在结构上具有一定的优势,极大地减少了外部干扰和辐射损耗,提供了更高的品质因数和测量精度。同时整个测量装置尺寸小巧,仅为22 mm×42 mm,便于携带,易于加工,具有一定的应用前景。
