基于ARIMA 模型的区间道路短时车流量预测研究

杨东龙

（天津大学，天津 300072）

随着机动车数量呈指数形式增长，尤其是在上下班高峰期及节假日时期，城市道路堵塞严重，增加了居民的出行成本，使道路交通面临着巨大的压力[1]。运用智能交通系统是缓解目前问题的有效措施，而精准的实时车流量预测是发展智能交通的重要环节[2]。

根据时间维度的不同可以将车流量的预测划分为长时（年）车流量预测、中时（月/日）车流量预测和短时（时/分）车流量预测[3-5]。长时及中时车流量数据的周期性较强、随机干扰较弱，而短时车流量的数据具有高度不确定性，预测较为困难且精度不高[6]。目前，用于短时车流量预测的模型[7-8]大概分为两类：一类是通过多影响因子进行车流量曲线的拟合，包括XGboost、GBDT、随机森林等，该类模型依赖于影响因子的选取，在现实中难以完全获取相应数据；另一类是基于内生变量本身进行预测，包括ARIMA、LSTM、KNN 等，该类模型数据获取成本低，易于实现[9]。

文中基于ARIMA 算法[10-12]提出了一种改进型的短时车流量预测模型。ARIMA 算法只在下一个周期有较好的预测表现，该改进模型根据需要预测的时间周期个数，将短时车流量数据划分为对应的数据集组，每个数据集组预测下一个时间周期的车流量，从而实现多个时间周期的准确预测。仿真实验证明了该改进算法的普适性和准确性。

1 ARIMA算法

短时车流量预测属于时间序列预测[13-14]，这一类预测建模相对一般的回归模型更加复杂，因为时间序列的数值是按照时间先后顺序进行排列的，预测值依赖于时间次序。自回归移动平均（ARIMA）算法是一种典型的时间序列预测算法。ARIMA 的基本原理是在时间序列平稳化的过程中，对因变量的滞后值、产生随机误差的滞后值及当前值进行预测。ARIMA 的五大核心概念为平稳性、自回归、移动平均、自回归移动平均、差分。

1）平稳性：指时间序列yt在n阶以下的所有矩取值均与时间无关，ARIMA只适用于平稳的时间序列。

2）自回归（Autoregressive，AR）：指利用自生变量的历史时间数据对未来时间数据进行预测。p阶自回归公式如下：

式中，μ表示常数项；εt表示误差项；λi表示自相关系数。

3）移动平均（Moving Average，MA）：指通过自回归模型中误差项的累加实现预测中随机波动的有效消除。q阶移动平均的计算公式如下：

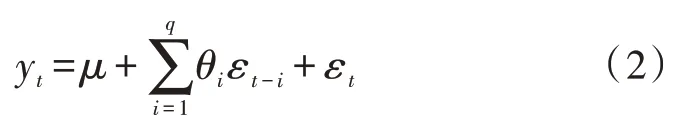
式中，μ表示常数项；εt表示误差项；θi表示误差项系数。

4）自回归移动平均：即AR 与MA 的结合，表示为ARMA(p,q)，公式如下：

5）差分（Integrate，I）：指时间序列的当前值减去滞后值，d阶差分公式表示如下：

ARIMA 的建模流程如图1 所示。其要求时间序列数据是平稳的，若数据不平稳，则需要进行差分。在确定了合适的d值以后，算法就转化为求解平稳时间序列Δdyt的问题，然后再将Δdyt构建为ARMA(p,q)，加上差分次数即可表示为ARIMA(p,d,q)。其中，p表示自回归阶数；d表示差分次数；q表示移动平均阶数。本质上，ARIMA 先对拟合值进行线性相加，再通过自身变量进行预测。

图书馆服务理念要突破传统图书馆在空间、时间、人员等方面的限制，为高校师生的教学科研服务、为师生的专业拓展服务。2015年7月，由美国新媒体联盟编写的，北京开放大学翻译的《新媒体联盟地平线报告（2015高等教育版）》指出：未来的几年内，正式学习和非正式学习融合，更多的移动学习和在线学习在高校广泛应用。现在已经有很多人通过互联网听到、看到、感受到在线教育的便捷。它因为具有名校名师效应、免费、高质量的优势，成为当下流行的课程选择。笔者认为，在线教育不仅仅是一种课程形式，它在本质上是互联网+知识的共享形态。图书馆在互联网+时代的服务应该与网络资源结合，更好地为师生利用网络提供高效、便捷的服务。

图1 ARIMA算法流程图

2 短时车流量预测模型

2.1 数据准备

图2 为区间道路3 天的车流量数据图，数据时间间隔为15 min，该区间3 天总车流量共59 513 辆，平均每天19 838 辆。从图中可以看出，每天6:00 之前区间道路车辆数量较少，每天8:00 和18:00 左右有1～2 小时的早晚高峰，且车流量较大。因此，选取第一天6:00 到第三天18:00 时间段的数据作为训练集，来预测下一个小时内每隔15 min 的车流量。

图2 短时车流量数据图

2.2 平稳性和非白噪声检验

ARIMA算法只适用于平稳的非白噪声时间序列，因此需要对训练集进行平稳性和非白噪声检验[15-16]。

文中采用ADF 进行平稳性检验（单位根检验）。当判断序列是否平稳时，首先观察第二部分显著性p_value。若p_value 小于0.05，则证明单位根有解，即表示时间序列平稳；若p_value 比0.05 大，则证明非平稳；若p_value 接近于0.05，则要通过τ值与临界值进行综合判断[17]。

稳定性检验后再进行非白噪声检验，并返回白噪声检验结果标志参数P值。若P值小于0.05，则表示在95%的置信水平区间拒绝原假设，证明时间序列为非白噪声序列；否则，时间序列为纯随机序列，无法进行预测。

2.3 时间序列定阶

为了确定ARIMA（p,d,q）模型中的p、q值，研究中采用自相关函数（ACF）和偏自相关函数（PACF）判断模型阶数法。求取训练集差分后平稳序列的ACF 和PACF，如图3 所示。

图3 自相关和偏自相关图

根据自相关和偏自相关图，结合表1 确定训练集的ARIMA 模型p、q值分别为1、0。确定 后进行ARIMA 模型拟合预测，即可得到未来1 个小时内每15 min 的预测值。

表1 ARIMA模型选择方法表

3 改进型预测模型

图4 改进模型训练集组1～4

4 模型评估结果

4.1 评价指标

构建适合短时车流量预测模型，实质上需要对不同模型的预测值和真实值通过量化的指标进行评价，即评估不同模型预测值的准确程度[19]。研究中选取了MAPE 与MAE 作为评价指标。

MAPE，即平均绝对百分比误差，其公式为：

式中，yi为真实值，为预测值，n为样本量。MAPE的取值范围为[0,+∞)，通常MAPE=0%表示完美模型，MAPE＞10%表示劣质模型。

MAE 为平均绝对误差，评估的是真实值和预测值的偏离程度，即预测误差的实际大小。MAE 的值越小说明模型越优，预测越准确，表达式为：

4.2 评价结果

采用经典ARIMA 模型和基于ARIMA 的改进模型分别对短时车流量数据集进行训练，并对未来1个小时内每15 min 的车流量进行预测。预测结果如图5 所示。由图5 可知，改进模型的预测效果明显优于经典模型，改进模型的拟合程度更高。

图5 不同模型预测结果

分别计算不同模型的MAPE 及MAE 值，如表2所示。经典模型的MAPE 值为12.176 5%，MAE 值为73.212 6，属于劣质模型，对短时车流量的预测值不具有参考价值。改进模型的MAPE 值为4.019 6%，MAE 值为22.468 1，说明基于ARIMA 的改进模型在一定程度上对经典模型进行了优化。

表2 不同模型MAPE、MAE值

5 结束语

文中基于经典的ARIMA 算法，针对其只在下一周期有良好预测表现的特点，通过划分数据集组的方式，使短时车流量曲线更加平滑，实现未来1 个小时内每15 min 车流量的预测。仿真验证了该改进模型的正确性与适用性，预测准确率能够达到95%以上，且改进模型无需依赖外部因子，调参方式简单，可适用于任何场景的车流量预测。后期将对改进模型进行优化，利用LSTM、Prophet 等时间序列预测算法的优点与改进模型进行融合，进一步降低MAPE、MAE 值，提高预测的准确率。