带干扰的一类混沌系统的脉冲控制与同步

胡茂萍

(重庆师范大学 数学科学学院,重庆 401331)

文献[1]提出了一类混沌系统

x1,x2,x3是状态变量,当a＝16,c＝24,d＝4,b∈R 和x1(0)＝1,x2(0)＝－1,x3(0)＝－3时,系统(1)是混沌的。当b ＜0时,系统(1)是广义Lorenz 系统族;当b＝0时,系统(1)是广义Lü 系统族;当b ＞0时,系统(1)是广义Chen 系统族。文献[1]研究了它的动力学行为,但没考虑系统在干扰因素下的行为,本文探讨系统在扰动的前提下如何利用脉冲控制技术来镇定系统。

1 基本定义与预备知识

脉冲微分系统如下

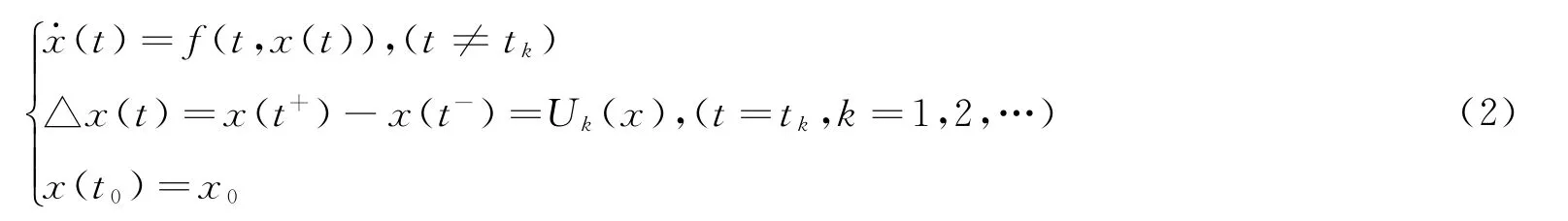
x ∈Rn,f∶R＋×Rn→Rn连续,Uk∶Rn→Rn是状态在tk的改变量,x(tk－)＝x(tk)。{tk}满足0＜t0＜t1＜t2＜…＜tk＜tk＋1＜…,当k →∞时,tk→∞,为了方便叙述,用x 代替x(t)。

定义1[2]设V∶R＋×Rn→R＋,则V 属于V0类,如果V 在(tk－1,tk]×Rn(k＝1,2,…)连续,且对每个x ∈Rn成立,存在;V 在x 是满足局部Lipschitz条件。

定义2[2]对(t,x)∈(tk－1,tk]×Rn,

定义3[2]设V ∈V0,且D＋V(t,x)≤g(t,V(t,x)),(t ≠tk),V(t,x ＋Uk(x))≤ψk(V(t,x)),(t＝tk)。其中g∶R＋×R＋→R 连续,ψk∶R＋→R＋非递减,

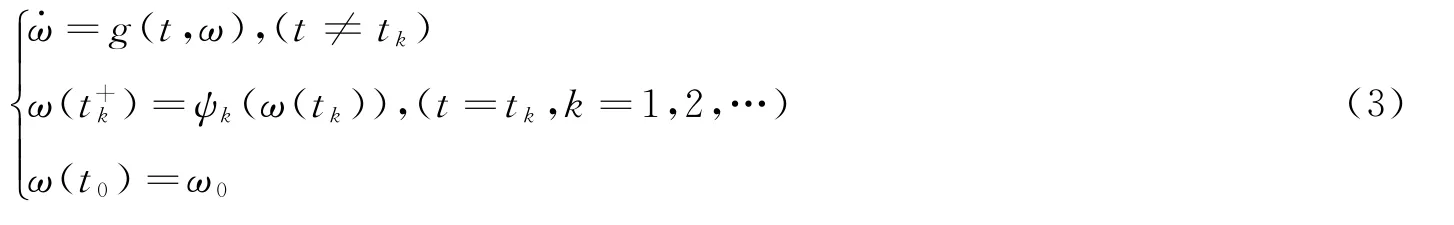
系统(3)称作系统(2)的比较系统。

定义4[2]若函数α(x)属于K 类,则α ∈C[R＋,Rk],α(0)＝0,α(x)是严格递增的。

引理1[2]若下面1)－3)满足:

1)V∶R＋×Sρ→R＋,ρ ＞0,V ∈V0,D＋V(t,x)≤g(t,V(t,x)),(t≠tk);

2)存在ρ＞0,当x ∈Sρ0时,对任意k 有x＋Uk(x)∈Sρ0和对x ∈Sρ0,t＝tk有V(t,x＋Uk(x))≤ψk(V(t,x));

3)存在α(˙),β(˙)∈K,在R＋×Sρ上有β(‖x‖)≤V(t,x)≤α(‖x‖),Sρ＝{x∶x ∈Rn,‖x‖ ＜ρ,ρ ＞0,‖˙‖ 为欧氏范数}。

则由系统(3)的稳定性能推出系统(2)的稳定性。

引理2[2]设g(t,ω)＝(t)ω,λ(t)∈C1[R＋,R＋],ψk(ω)＝dkω,dk≥0,如果:

1)存在γ ＞1有λ(tk＋1)＋ln(γdk)≤λ(tk)(k＝0,1,…);

2)λ(t)满足λ˙≥0,则系统(3)渐近稳定。

2 混沌系统的脉冲稳定

把方程(1)重写如下:

其中w(t,x)为干扰项,满足‖w(t,x)‖ ≤L‖x‖(L ＞0),x＝(x1,x2,x3)T,且:

有脉冲控制的系统为

其中{tk}满足0＜t0＜t1＜t2＜… ＜tk＜tk＋1＜…,当k →∞时,tk→∞,△tk＝tk＋1－tk,k＝1,2,3,…,设计△x(tk)＝uk(x)＝－ξ△tkx(tk)。

定理1设q＝λmax(A ＋AT),dk＝(1－ξ△tk)2,|xi|≤M,i＝1,2,3,p＝q＋2M ＜＋1＋L2,如果γ ＞1使得:

1)|1－ξ△tk|＜1;

2)p△tk＋ln(γdk)≤0成立,系统(6)渐近稳定。

证明取Lyapunov函数V(t,x)＝xTx,则当t≠tk时,

故令g(t,ω)＝ρω,当ρ0 ＞0,x ∈Sρ0时,有‖x ＋uk(x)‖＝‖x－ξ△tkx‖＝|1－ξ△tk|‖x‖ ＜‖x‖。故(x＋uk(x))∈Sρ0。

当t＝tk时,

令ψk(ω)＝dkω,所以(6)的比较系统为:

由于定理1中p△tk＋ln(γ△dk)≤0,根据引理1、引理2得出系统(6)渐近稳定。

3 混沌系统的脉冲同步

主系统由(4)确定,从系统为:

设计△e(tk)＝uk(e)＝－ξ△tke(tk),△tk＝tk＋1－tk,k＝1,2,3,… 。

定理2设q＝λmax(A ＋AT),dk＝(1－ξ△tk)2tk＋1－tk,|xi|≤M,i＝1,2,3,p＝q＋1＋S2＋3M,如果γ ＞1使得:

1)|1－ξ△tk|＜1;

2)p△tk＋ln(γdk)≤0成立,系统(8)与(4)实现脉冲同步。

证明取Lyapunov函数V(t,e)＝eTe,当t≠tk时,

故令g(t,ω)＝ρω,当ρ0 ＞0,当e∈Sρ0时,‖e＋uk(e)‖＝‖e－ξ△tke‖＝|1－ξ△tk|‖e‖＜‖e‖。

因此有(e＋uk(e))∈Sρ0。当t＝tk时,

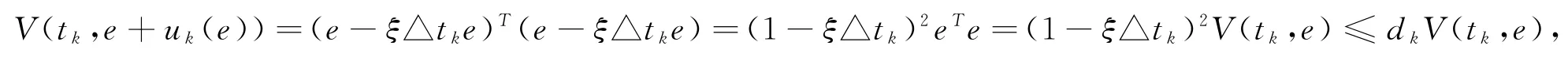
故取ψk(ω)＝dkω,系统(10)的比较系统为:

由于定理2中p△tk＋ln(γ△dk)≤0,又根据引理1、引理2知系统(10)渐近稳定,故系统(8)与系统(4)实现脉冲同步。

4 数值例子

系统(1)中当b＝16时。

例1q＝32,M＝20,此时取L＝1,γ＝2,ξ＝35,△t1＝△t2＝…＝△tk＝…＝0.02,设计uk(x)＝－0.92x,那么|1－ξ△tk|＝0.3＜1;p△tk＋ln(γdk)≤0则由定理1得,系统(6)渐近稳定。

例2q＝32,M＝20,选取S＝1,γ＝1.1,ξ＝40,△t1＝△t2＝…＝△tk＝…＝0.02,则uk(e)＝－0.92e,那么|1－ξ△tk|＝0.2＜1;p△tk＋ln(γdk)≤0则由定理2得,系统(10)渐近稳定,从图1中可得系统(8)和系统(4)能快速达到脉冲同步。

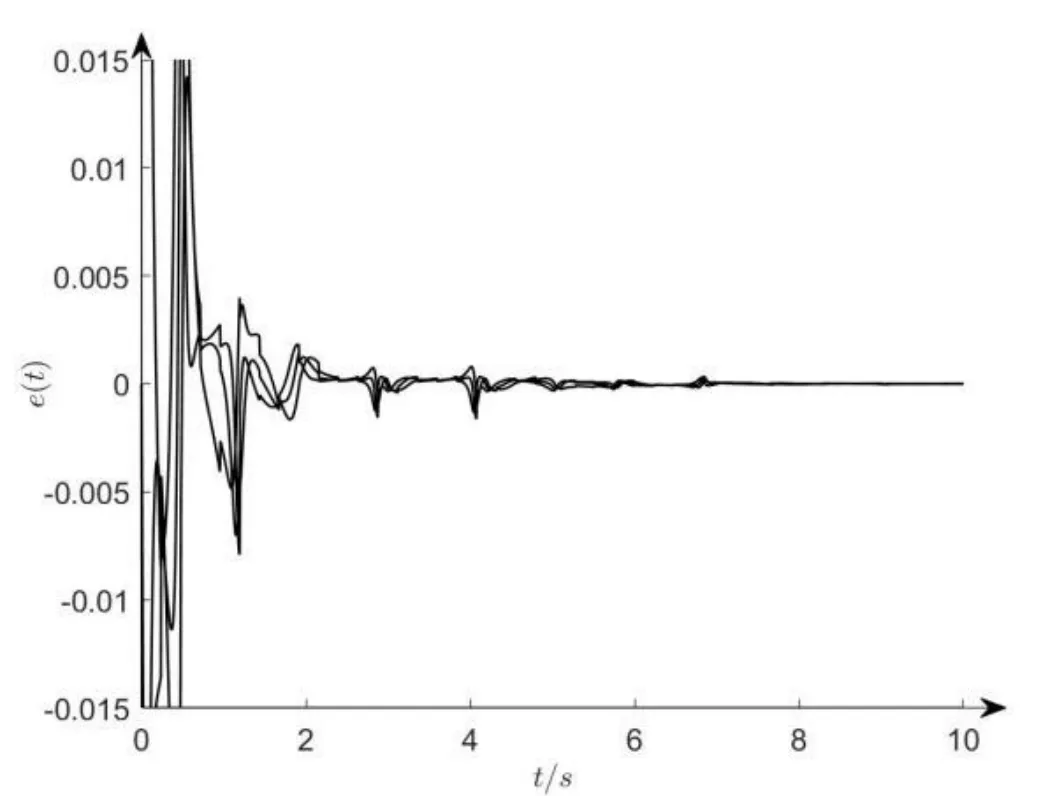
图1 误差系统(10)的状态曲线

5 结论

考虑有干扰的一类混沌系统在脉冲控制下的稳定与同步问题,得到了两个定理,并通过仿真实验说明定理有效性。