数学专业多元微积分教学的几点体会
2021-07-09刘轼波
刘轼波
(厦门大学 数学科学学院,福建 厦门361005)
1 引 言
数学分析是数学类专业本科生最重要的基础课,因此各高校的数学院系对这门课都极为重视.2009年,我国启动基础学科拔尖学生培养试验计划.从2014年秋季起,厦门大学数学科学学院对入选该计划的本科生的主要课程实行小班教学,由笔者负责该班二年级第一学期的数学分析(即数学分析3)的教学工作.这门课的主要内容就是多元微积分.为了行文方便,下文中的数学分析也专指多元微积分.
对这些优秀学生实行小班教学的意图,当然是希望在教学内容等方面突破传统教材的框架,力求有所创新,更好地完成数学人才培养任务.因此,对这门课进行了一些思考和探索,逐步形成了有特色的课程内容体系,在几年的教学过程中形成了一份讲义.此外,还与教过的本科生合作,发表了两篇关于多元微积分的论文[1-2];这些结果现在已经成多元微积分的标准内容.此外,我在北京大学、北京师范大学、南京大学和浙江大学等高校为本科生做有关的学术报告,介绍我们在数学分析方面的工作;2017年、2018年和2020年应邀在复旦大学举办的数学分析教学研讨会做报告.
2019年6月,我应邀在国家天元数学东南中心举办的数学专业课程建设研讨会做报告(研讨会网址: http:∥tianyuan.xmu.edu.cn/activities/19-20/sxkc2019/index.html).本文是根据这个报告的内容整理而成.
2 课程现代化及与现代数学的联系
现代数学很多内容都是高维的,适应向量记法并能熟练操作向量值函数,是成为优秀数学家必须的素养.因此,在讲授多元微积分时,特别强调向量的记法以及向量值函数.可能很多人都已经意识到:数学分析中很多概念和定理,用分量形式表达非常繁琐,而用向量形式则非常简洁,并且更能凸显数学内容的实质和内在联系;这应该已经成为很多同行的共识了.除此之外在教学中还进一步发现:若不涉及向量值函数,则无法充分展现微分学的基本思想!这一点将在下文进一步阐述(见注4). 由此可见,在多元微积分教学中仔细讲解向量值函数,是在教学中应该提倡的一项举措.
数学分析通常被认为是一门古老的学问.其实,只要细加研究,是可以发现数学分析的内容与现代数学的一些联系的.在教学中,应该善于找到这些联系并展现给学生.以下结合自己的教学实践举几个例子.
由于本文涉及的问题较多,以下十余个例子中所给的证明只是对证明思路的大致描述,一些细节因篇幅所限不得不省略.相信这些简略的文字足以使读者理解解决这些问题的想法.
例1m中不存在既开又闭的非空真子集.
证设m的非空子集U既开又闭,U≠m.取a∈mU,因U闭,有x∈U使
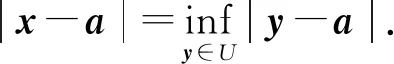
因U开,可在x附近取点x′∈U使|x′-a|<|x-a|;这就与上式矛盾.
在数学分析课中介绍这个简单的例1,是为了得到以下经典结果.
例2设f∶m→m是C1-映射,对∀x∈m,detf′(x)≠0.若f是强制的,即|x|→∞时,|f(x)|→∞,则f(m)=m.
证事实上,运用反函数定理,由f的Jacobi行列式处处非零可知f的值域为开集;由f强制可知f的值域为闭集.因此由例1即知f的值域是m.
注1 例2的结论相当于对∀b∈m,都有x∈m使f(x)=b.因此例2可以看作非线性代数方程组的求解问题.此例也可以通过研究φ∶x|f(x)-b|2的最值来证明.进一步,对φ应用山路定理[3],还可以证明在例2的条件下f是单射,因此f∶m→m是微分同胚,详见[4].
鉴于方程的求解是数学的中心问题,以及例2的简单性,任何学过多元微积分的数学类本科生都应该至少知道例2的上述两种证明方法.不幸的是在某些985高校,即使是入选拔尖计划的优秀学生也完全不知道这个例子.
注2 在[1]中,把例2的结论推广为:设n≥2,f∶m→n是C1-映射,仅有至多有限个x∈m使rankf′(x) 变分方法在近现代数学中有重要的地位.在多元函数积分学部分,作为散度定理的应用,可以用变分的思想推导极小曲面方程;这是把泛函极值问题转化为求解偏微分方程.为了研究数学、物理中一些重要的非线性偏微分方程解的存在性,也可以反其道而行之,把方程求解的问题归结为寻找某个能量泛函的极值点或更一般的临界点,这就是非线性微分方程的变分方法[5-6].在数学分析这样的基础课中当然不可能过多涉及偏微分方程,但是通过研究非线性代数方程来展示变分方法的威力,应该是很有趣的. |F(x)|≤C(1+|x|θ), f=∇F∶m→m.则非线性代数方程组 即Ax=f(x)有解. 证考虑C1-函数Φ∶m→,·x-F(x).则|x|→∞时,Φ(x)→+∞,于是Φ在m中的某点ξ达到最小值.由多元函数极值的必要条件(Fermat定理)有∇Φ(ξ)=0,即Aξ=f(ξ).这ξ就是Ax=f(x)的解. 作为在[2]中给出的m-重积分换元公式新证明的简单推论,立刻得到m-维Brouwer不动点定理(见注10). 不动点理论也是现代数学中的重要内容,应用Brouwer不动点定理可以改进例3的结果.在以下的例4中,A不必是对称矩阵,f也不必是某个数量值函数F的梯度. 例4设A是m-阶可逆矩阵,f:m→m连续且 (1) 则非线性代数方程组Ax=f(x)有解. 设b∈m,常值映射f∶xb显然满足例4要求的条件.于是由例4可知当A是可逆矩阵时,非齐次线性方程组Ax=b有解.因此例4可以看作线性代数中的Cramer法则的非线性推广.方程组Ax=f(x)的求解问题等价于求映射g∶xA-1f(x)的不动点.运用(1)可以找到充分大的r>0使这里是球心在原点半径为r的闭球,于是可以应用Brouwer不动点定理得到的不动点.具体细节留给读者. 进行多元微积分的教学,当然应该透彻地讲清楚微积分的基本思想,把它展现在学生面前.先来谈微分学,首先回顾一下非线性映射f∶m→n在点a∈m的导数的概念.如果有n×m矩阵A,使得当h→0时 f(a+h)-f(a)=Ah+o(|h|), (2) 就称f在点a可微;并将由此性质唯一确定的A称为f在a的(全)导数,记为f′(a).熟知,A其实就是f在a点的Jacobi矩阵.当然,也可以把A=f′(a)视为m到n的线性映射. 从定义来看,线性映射f′(a)是非线性映射hf(a+h)-f(a)的近似,因此有时也称其为f在a点的线性化.由于线性映射比非线性映射容易研究,很自然就希望能够通过考察f′(a)来研究f. 我们认为微分学的基本思想就是通过研究非线性映射f∶m→n在点a的导数f′(a)来推断f在a附近的局部性质.大体上说:f′(a)如何,f就大约如何(见例5).这里需要向学生强调的是,由于f在a点的可微性以及其导数的值都只与f在a点附近的行为有关,所以只能期望得到f在a点附近的局部性质.下面来看一个典型的例子.为了方便起见,用Na表示含a的开集构成的集族. 例5设Ω∈Na,f∶Ω→n是Ck-映射. (i) 若f′(a)∶m→n可逆(必m=n),则f在a局部可逆.即有U∈Na及V∈Nf(a)使f∶U→V是双射,且f-1也是Ck-映射; (ii) 若f′(a)∶m→n是满射(必m≥n),则f在a局部满.其确切含义是:b=f(a)是f(Ω)的内点.也就是说b点附近的点都在f的值域中,称这个结论为局部满射定理.特别地,如果对∀x∈Ω,f′(x)都是线性满射,则f(Ω)是n的开子集; (iii) 若f′(a)∶m→n是单射(必m≤n),则f在a局部单. 注3 结论(i)正是反函数定理.结论(ii)、(iii)则是其推论;它们以及更一般的秩定理,都可以通过补充分量的方法转化为相同维数的空间之间的映射,然后应用反函数定理来证明.这是应用反函数定理的典型手法. 注4 例5是体现微分学基本思想的最佳范例:它很好地表现了f′(a)如何,f就大约如何这个思想.只有用向量值函数,才能把它表达得如此简练、清楚.如果按传统的教法,只讨论数量值函数(即n=1的情形),则情形(i)、(iii)不可能出现,而情形(ii)也只在f′(a)≠0这个平凡的情形出现,因此就没法通过这个最佳范例展现微分学的基本思想,这无疑是一个巨大的损失. 局部满射定理、局部单射定理以及更一般的秩定理,对学生今后学习微分流形非常重要.因此在数学分析课中应该不回避向量值函数、把这几个并不困难的定理讲清楚.这样一来,数学分析的教学才能进入广阔的新天地.例如,郑州大学马建国编著的教材[7]中用局部满射定理给出约束极值的Lagrange乘数法的一个有趣的几何证明;注2中提到的工作[1]也是用局部满射定理证明的. 下面来谈谈多元函数积分学.积分学用于实际问题的关键是微元法,我们认为这就是积分学的基本思想.至于各种积分的性质和计算方法乃至它们之间的关系形成的整套理论体系,当然也很重要,但大家在教学中都对此给予了足够的重视.所以下面着重谈一下微元法. 例6(曲面的面积) 利用Gram-Schmidt正交化可以定义并证明m中以a为顶点,以线性无关向量组为边的平行2k-面体Pa[v]=Pa[v1,…,vk]的体积为 (3) 其中G=(v1,…,vk)是以vi为列向量的m×k矩阵. (ii) 模掉一个平移,x′(u0)∶k→m则将Pu0[du]映成S在x0=x(u0)的切空间Tx0S中的小2k-面体Px0[v].这里·x′(u0)εi.用Px0[v]的体积来近似dσ(这是微元法的要点),则得到面积微元 dσ≈μ(Px0[v]) =du1…duk·μ(Px0[x′(u0)ε1,…,x′(u0)εk]) (4) 这里第二个等号用了(3).第一个等号用到由(3)容易推知的事实:将平行2k-面体的某边伸缩为原来的λ倍,则其体积变成原来的λ倍;见例8. 很自然,当u0跑遍U时,把面积微元dσ累积起来,就得到m中k-维曲面S的面积 运用k-重积分换元公式,很容易证明上式右端的k-重积分与曲面S的参数表示的选择无关.因此这样来定义m中k-维曲面S的面积是合理的. 以下介绍的余面积公式通常并不是数学分析课的教学内容,但是南京大学梅加强编著的教材[8]中对它做了简单的介绍.鉴于这个公式非常有用,在课程中运用学生正在学的常微分方程(在我校安排在二年级第1学期)的知识证明了余面积公式,见例13.这里先用微元法形式上做些推导. 例7(余面积公式) 设G⊂m是开区域,f∶G→.视Ω=f-1[a,b]为m中的物体,g:Ω→是密度函数.则Ω的质量 任取t∈[a,b].在曲面f-1(t)上的点x取面元dσ.过x作法线交邻近的曲面f-1(t+dt)于y.则 dt=f(y)-f(x)≈∇f(x)·(y-x), 这里用到f在x的Taylor展开并略去高阶无穷小量.由于∇f(x)和y-x都是曲面f-1(t)在x处的法向量,即它们是共线的,在上式两边取模得到 用x处的密度g(x)来近似代替以dσ为底,|y-x|为高的柱体中各点的密度.这柱体的体积dV和质量dm分别等于 将dm沿曲面f-1(t)积分,就得到环状区域f-1[t,t+dt]的质量 现在在[a,b]上对t积分,就得到Ω的总质量 (5) 这就是余面积公式.它其实就是化重积分为累次积分,只不过里层积分在一个曲面上进行. 注6 本例在两个层次上运用微元法.先取t方向的微元dt,然后在曲面f-1(t)上点x处取面积微元dσ,得出小柱体dV的质量微元dm后对dσ积分得到环状区域f-1[t,t+dt]的质量dM,再对dt积分得到整个区域f-1[a,b]的质量.因此,这是微元法比较复杂的应用,但是把它介绍给学生能很好地加强对微元法的理解,从而提高运用积分解决实际问题的能力. 微元法的另一精彩应用是由Gauss公式推导Archimedes浮力定律.这是欧阳光中等编著的教材[9]中的一道例题,也是陈纪修等编著的教材[10]中的一道习题.因此我们这里就略而不谈了. 在我国大部分高校数学院系的课程设置方案中,数学分析3(即多元微积分)一般被安排在二年级第一学期.此时,学生已经学完了线性代数.传统的数学分析课运用了一些线性代数的知识,主要限于用线性映射和矩阵表达非线性映射的导数(见(2))、用矩阵乘法表达复合函数求导的链锁法则,以及通过考察函数在临界点处的Hesse矩阵的正定性来研究极值.文[11]对微积分与线性代数教学的互相促进关系做了很好的阐述.另外,在很多学校二年级第一学期的学生同时在学习常微分方程,但是根据对国内外微积分或数学分析教学的了解,没有看到将常微分方程的知识应用于数学分析教学的做法. 在教学中发现线性代数可以对数学分析的教学发挥更大的作用.此外,近年的教学中运用学生刚刚掌握的常微分方程知识来处理数学分析中的一些重要问题,也取得了很好的效果.以下分别介绍这两方面的典型例子. 例8(初等矩阵的妙用) 在(3)中给出了m中的平行2k-面体体积的计算公式.在应用中往往需要用到平行多面体的体积的性质,这些性质可以利用公式(3)结合初等矩阵来得到.例如,讨论m中k-维曲面的面积时,在(4)式需要以下等式 μ(Pa[v1,…,λvi,…,vk])=|λ|μ(Pa[v1,…,vi,…,vk]). 例9(超曲面的法向量) 设U是m-1中的开集,来求m中以正则C1-映射x∶U→m为参数表示的曲面S在点x0=x(u0)的法向量N. 对∀h∈m-1,γ∶tx(u0+th)是S上过x0的曲线,其切向量为 由于N与γ′(0)正交,有 0=γ′(0)·N=(x′(u0)h)·N=hT([x′(u0)]TN). 由h的任意性可知[x′(u0)]TN=0.法向量N至少有一个非零分量,于是此式实际上是以剩余m-1个分量为未知量的非齐次线性方程组.由x正则即rankx′(u0)=m-1可知此方程组的系数行列式非零,于是由Cramer法则可求出法向量 注7 大部分数学分析教材只用三维空间中向量的叉乘讨论m=3的情形,有些教材(例如[8])运用学生比较陌生的(m-1)个m-维向量的叉乘讨论m-维情形.例9用学生熟悉的线性代数来研究,显得更为自然.作为课后的练习还可以让学生运用关于k个含m-1个未知数的非齐次线性方程组的理论研究m中k-维曲面的法向量问题. 定向是流形等一些数学对象的一个整体性质.常常说Jacobi行列式大于零的映射保持定向,指的是:设φ∶m→m,a∈m,detφ′(a)>0,若是Tam的正基,则是Tφ(a)m的正基.以下的例10从另一个重要的角度讨论Jacobi行列式的符号与定向的关系. 例10(Jacobi行列式的符号与定向) 设Ω和D是m中的光滑闭区域,φ∶Ω→D是微分同胚.设U是m-1中的开集,x∶U→∂Ω是∂Ω在点a∈∂Ω附近的局部参数表示,熟知y=φ∘x∶U→∂D是∂D在b=φ(a)附近的局部参数表示.若detφ′(a)>0,并且 是∂Ω在a点的外法向量,则 是∂D在b=φ(a)点的外法向量. 注8 设N是∂Ω在a∈∂Ω的法向量.若有ε>0,使得当t∈(-ε,0)时a+tN∈Ω°,就称N是∂Ω在a处的外法向量.例10的关键是证明D中的曲线γ∶tφ(a+tN)在b=φ(a)的切向量v与的夹角是锐角.为此运用了扁矩阵与瘦矩阵之积的行列式的Cauchy-Binet公式,以及A*A=(detA)Im等线性代数知识;这里A*是A的伴随矩阵,Im是m-阶单位阵. 例11(重积分换元公式) 设D和Ω是m中Jordan可测的有界闭区域,φ∶Ω→D是C1-微分同胚.若f∈C(D),则有m-重积分的换元公式 (6) 重积分换元公式的证明是数学分析教学中比较困难的问题.do Carmo的名著[12]中有一道习题,让读者用Green公式证明二重积分换元公式.受其启发,[2]中把这道习题的思想推广到高维,用数学归纳法给出m-重积分换元公式(6)的一个比较简单的证明. 其中x∶U→m是曲面S的参数表示,N是由此参数表示按例9给出的S的法向量场.由归纳假设,即(m-1)-重积分换元公式,容易证明上式右端与S的参数表示的选择无关. 然后,利用化重积分为累次积分容易证明m-维散度定理.最后利用散度定理证明m-重积分换元公式,这时需要用到Cauchy-Binet公式,行列式按行展开等线性代数知识. 注9 与划分积分区域并估计每个小块变换后的体积,进而研究Riemann和的传统证明相比,在[2]中给出的上述证明完全是巧妙的计算,便于课堂讲授,学生也容易掌握.这个证明基于链法则和微积分基本定理(即散度定理),在思想上与一元情形(即定积分)是一脉相承的.因此,有一定理由相信这是证明重积分换元公式最合理的办法. 在证明的过程中,顺便建立了(第一类)曲面积分的理论,包括m-维的散度定理.因此从需要的学时来看,可能比其他方法会节省一些.利用曲面的参数表示将曲面积分定义为参数区域上的(m-1)-重积分,是近些年来很多数学分析教材(例如[8,9,13,14])采用的做法.当然,这些教材需要先用其他方法证明重积分换元公式,以保证曲面积分的定义与曲面的参数表示的选择无关. 注10 在证明中,当Ω是球体时,只要求换元映射φ将∂Ω微分同胚地映成∂D,也就是说φ∶Ω→D可以既不单也不满.于是,用[15]中的想法立刻就得到m-维Brouwer不动点定理.据我所知,国内外出版的数学分析教材中几乎都没能探讨高维的Brouwer不动点定理,除非先花大量篇幅介绍微分流形、微分形式以及流形上的积分和Stokes公式(见Zorich [16]). 张筑生教授的教材[17]用Green公式证明了二维的Brouwer不动点定理.关于Brouwer不动点定理的其他初等证明(即只用微积分),可见[18-19]. 设g∈C1(m),∀x∈S=g-1(0)有∇g(x)≠0,则S是m中的光滑曲面,设p∈S.众所周知,∇g(p)与S上任一经过p点的曲线γ的切向量γ′(0)都正交,因此∇g(p)是S在p点的法向量.一个自然的问题是:设h∈m,∇g(p)·h=0,S上是否有经过p点的曲线以h为切向量?这个问题与约束极值的Lagrange乘数法有关.对此,有如下结果. 例12设g∈C2(m,n),p∈S=g-1(0),rankg′(p)=n.若g′(p)h=0,则有C1-映射γ∶(-ε,ε)→S使γ(0)=p且γ′(0)=h. 利用这个结论,可以研究f∈C1(m)在约束条件g(x)=0下的约束极值问题,证明Lagrange乘数法.一些数学分析教材运用隐函数定理给出例12的证明,这是隐函数定理的漂亮应用,课上当然也会讲.但是.我们还运用常微分方程的方法给出如下证明. γ′(t)=Y(γ(t)),γ(0)=p (7) 有解γ∶(-ε,ε)→m,显然γ(0)=p,γ′(0)=Y(p)=h. 用Gram-Schmidt正交化将向量场Y用∇gi线性表示,并利用(7)以及g′(p)h=0容易验证(g∘γ)′(t)=0.故g(γ(t))=g(p)=0,即γ(-ε,ε)⊂S. 注11 要求g∈C2(m,n)是为了对(7)应用常微分方程解的存在唯一性定理.如果用隐函数定理来证明的话,只需要求g∈C1(m,n).上述证明是受[20]第3章启发做出的,那里考虑的是n=1的情形,此时 在例7中曾用微元法导出余面积公式.作为常微分方程对数学分析的应用的另一个例子,现在来证明余面积公式. 例13(余面积公式) 设G⊂m为有界开集,f∈C2(G),Ω=f-1[a,b].对任意x∈Ω有∇f(x)≠0.若g∈C(Ω),则 证为简单起见只考虑f-1(a)有统一的参数表示的情形,设φ∶U→m是其参数表示.利用常微分方程初值问题 (8) 的解x=x(t,p)可构造微分同胚T∶U×[a,b]→Ω,(u,t)x(t,φ(u)).利用行列式按列展开、共线向量内积的绝对值等于它们的模之积以及(8),容易算出 这里Nt是曲面f-1(t)的参数表示uT(u,t)按照例9的方式确定的法向量.于是由重积分换元公式和化重积分为累次积分即得 注12 上述余面积公式的证明与我的研究领域临界点理论[5]中的形变引理有密切关系.这个证明也可以看作伍洪熙等教授的书[21]第11章讲述的Riemann流形上的余面积公式在欧氏空间情形的初等版本.然而[21]中的证明需要很多微分流形和Riemann几何方面的预备知识,所以需要把这些高级的概念解包,整理成上述的初等证明,其中的一个关键之处是上述证明中提及的对detT′(u,t)的巧妙计算.给出的这个改编的证明把常微分方程、线性代数完美地结合起来,很值得玩味,应该会使学生受到很大的启发. 注13 在2018年秋季讲完余面积公式后,很惊喜地发现有学生运用这个公式给出如下关于等值面的Catalan公式的极简证明:设f∈C1(n),对∀v∈,等值面f-1(v)都是封闭曲面,设其所围立体的体积为F(v),并且F∈C1[a,b].则 当n≤3时,Catalan公式是林源渠、方企勤的习题集[22]中的题目.由于相应教材中没讲余面积公式,我的学生用余面积公式给出的证明当然不是[22]的作者期望的证明. 在数学分析课中系统地运用常微分方程的知识,应该说是一个大胆的尝试,在全世界可能都没有先例.在我国大部分高校,常微分方程与数学分析3都在二年级第一学期开设,因此,在数学分析3中运用常微分方程的知识是完全可行的.笔者认为这样做有助于培养学生对数学的整体观念和融会贯通地运用不同课程的知识来解决问题的能力. 数学类本科生在一年级主要学习一元微积分和线性代数.这两门课分别关注一维和高维,不太可能有实质性的交叉融合;因此一年级应该是打基础的阶段.但是正如已经看到的,在二年级第一学期,线性代数和常微分方程可以很自然地进入数学分析的教学,得到丰富多彩的结果.现在看来多元微积分应该是学生接触的第一门综合性的课程.这样的交叉融合,也有利于学生更好地理解线性代数和常微分方程.此外,很多学校的普通物理课在一年级第二学期和二年级第一学期开设,因此,正如[23]所倡导的,多元微积分的教学还可以与学生正在学习的物理学结合起来,使学生对数学和物理都有更好的理解. 本文中多次强调,数学分析中应该重视向量值函数.在注4中清楚地表明:对向量值函数避而不谈或讲得不够,就很难向学生充分展现微分学的基本思想.如果不熟悉向量值函数,学生也将错过数学分析中很多精彩的内容.在二年级第一学期,学生已经学完高等代数,不应该对处理向量和向量值函数有实质性的困难.也许是因为现有的大部分数学分析教材都回避向量值函数(或把它作为选学内容)的原因,有些教师担心学生接受不了;这种保守的观念应该改变. 本文谈到的这些体会和看法,虽然是这几年为厦门大学入选拔尖学生培养试验计划的优秀学生讲授多元微积分的过程中对这门课进行思考和探索而产生的,但是笔者认为这些想法和做法也完全适合其他的学生(包括非重点院校的数学类本科生).其理由是:在二年级第一学期,各类学生在知识储备上几乎没有差别.今后,希望能有机会把笔者对本门课程的教学经验应用到更广泛的学生群体,为数学教育事业做出应有的贡献. 致谢作者对多元微积分教学的想法曾得到北京大学张恭庆院士的关心并受他邀请到北京大学做报告.本文部分内容曾在一些高校为本科生做报告,并应楼红卫教授邀请在复旦大学举办的数学分析教学研讨会报告.作者衷心感谢张恭庆院士、楼红卫教授,以及安排作者与本科生交流的有关高校.此外,作者感谢审稿专家提出的宝贵意见.
3 充分展现微积分的基本思想
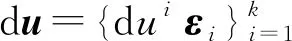

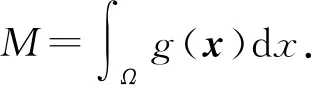
4 不同课程之间融会贯通
4.1 线性代数
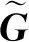
4.2 常微分方程
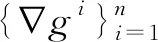
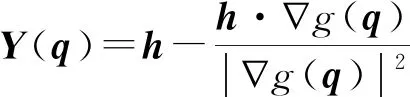
5 结 论
