Minitab在统计学专业实践课程中的案例拓展

束 慧， 徐宏光

(南京邮电大学 理学院，南京210023)

1 引 言

统计学专业实践课程是培养学生从“知识”到“应用”的重要环节，在整个统计学专业培养方案中具有不可替代的地位.近年来，一些新的、侧重理论学习与实践操作相融合的教学理念在国内高校中被广泛推广[1]，越来越多的高校统计学、数学方向的教师开始设计实践教学的新模型、新方法[2-3].作为一款商业统计软件，Minitab在统计学专业的实践教学中具有不可替代的地位，尤其是涉及到6σ管理等质量控制课程的实践时，其地位更加凸显，围绕Minitab设计的实践教学案例陆续涌现[4].

Minitab是由美国宾夕法尼亚州立大学开发的一款商用统计软件，其特色功能为质量控制模块，被广泛运用于工业企业的产品质量控制过程[5].以Minitab17版本为例，该软件的质量控制模块由控制图、质量控制两个子模块组成.在控制图模块中，整合了子组变量、单值变量、属性、时间加权、多属性变量以及稀有事件控制图等各类控制图的绘制功能.在运用Minitab绘制各类控制图时，控制限的选择是开放给用户的，提供了“标准差的倍数”或者指定“控制上、下限”的权限[5].这样的功能设计，具有操作上的简便性，但同时也增加了用户在绘制控制图时的随机性，尤其是绘制一些检测生产过程中的中小变异的控制图，如指数加权移动平均(Exponentially Weighted Moving Average，EWMA)[6-9]，累计和CUSUM (Cumulative Sum)[10-11]等控制图时，控制限设置存在一定的优化空间.

本文从统计学专业实践教学案例拓展的角度出发，对控制图的重要优化指标进行以Minitab为基础的算法设计和计算，并根据运算结果对控制图的关键参数进行优化选择.本文的研究既可以作为统计学专业实践课程的案例拓展，也可以作为Minitab统计软件质量控制模块功能优化研究，可以为统计学专业实践课程提供实践内容和实践工具两个方面的参考.

本文第二部分选取典型的控制图，简要介绍其优化指标的计算方法，以及基于指标的控制图优化原理；以理论方法为基础，设计控制图优化指标在Minitab上的实现算法，并提供一个案例计算结果；第三部分是本文的分析总结，基于文章的结果提供一些Minitab软件在高校统计学专业实践教学环节中的应用拓展建议.

2 实践案例构建——基于Minitab 的控制图优化

2.1 控制图优化理论模型

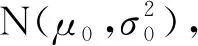
(1)

在进行质量检验过程中，如果抽样的时间间隔及样本容量n固定不变，则称相应的控制图为固定抽样率(Fixed Sampling Rate，FSR)控制图.对于一个FSR控制图，定义从检测开始到它发出生产变异的报警标识为止，抽取的平均样本组数为平均运行长度(Average Run Length， ARL).当过程可控时，质量控制图的报警就属于误报，可控的ARL越大越好；当过程失控时，质量控制图应尽早报警，失控的ARL越小越好.

2.2 控制图优化指标ARL的计算方法

控制图ARL的计算方法多样，研究较丰富，运用有限状态Markov链的平均首达时间计算ARL是比较常见的[6，7，12，13].这部分内容结合统计学专业实践环节教学要求，可以设置为对学生的统计学理论基础的考察项目.

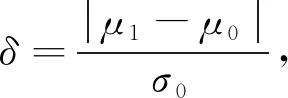
在上述前提下，控制上限可以表示为

UCL=L·σs=h，

(2)

相应的控制下限

LCL=-h，

(3)

其中，L为控制限参数，是优化控制图时的重要选择参数.

ARL计算的基本依据是有限状态Markov链从非吸收态首次转移到吸收态的平均时间，因此，需要对控制图界限进行Markov链状态空间转换.将控制图的上下控制限之间的区间分成k(奇数)个子区间，小区间的宽度d

(4)

Markov链的状态空间可以用{Ij}j=1，2，…，k表示，且设Ij为小区间的中心点

(5)

当EWMA检验统计量St落在第j个区间内时，即

就定义统计量St处于状态Ij.EWMA控制图是双边的，将大于上控制限h的区域与小于下控制限-h的区域这两个吸收域合并为一个.在上述设置下，该Markov链的一步转移概率pij为

pij=P{St+1∈Ij|St∈Ii}

phj=0，j=1，2，…，k;

phh=1.

(6)

检测统计量St在m时刻的一步转移概率阵为

(7)

矩阵P的最后一列表示从状态Ii出发一步转移到吸收状态Ih的概率，因此可记

以fih表示从状态Ii出发第一次转移到吸收状态Ih所需要的步数(首达时间)，fh=(f1h，…，f(h-1)h)T，则当检测统计量的初始态为Ii时的ARL值即为E(fh)的第i个分量，特别地，初始状态是从中心点出发，则为中间位置的分量.根据有限状态马氏链的平均首达时间计算方法，有

ARL=E(fh)=(I-R)-11，

(8)

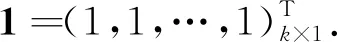
2.3 基于Minitab的ARL计算及控制图优化

根据上述理论模型，控制图优化的基本思路是：给定变异系数δ，状态空间划分k，优化参数：平滑系数λ、控制限L，使得控制图在受控态下(变异系数δ=0)的ARL较大，而失控状态(变异系数δ≠0)下的ARL较小，同时分析状态空间划分对相应的ARL优化的影响.

借助Minitab的数据整理、数据(矩阵)计算功能，以Minitab基于列变量的运算规则为语句设计特点，在Minitab宏命令“GMACRO”功能框架下，定义ARL计算过程脚本，设计基于Minitab的控制图优化指标ARL计算及反馈优化机制(图1).

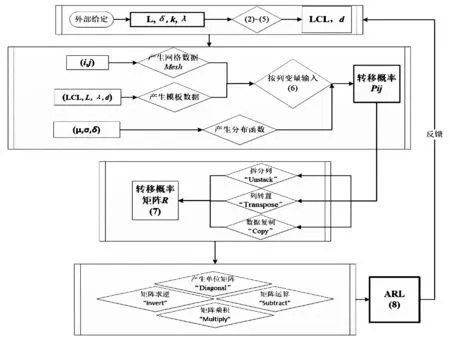
图1 基于Minitab的EWMA控制图优化指标计算及反馈

Step1 设置不同的控制限L，偏移系数δ，状态空间k，平滑系数λ值，计算相应的LCL，d;

Step2 在计算转移概率矩阵时，借助Minitab的“Mesh”命令，可以产生计算转移概率矩阵的网格化指标(i，j)，替代一般编程语言中的循环结构;

Step3 按列存储(i，j，LCL，L，λ，d)，其中的(LCL，L，λ，d)利用Minitab的产生模板数据，和对应的网格数据对一致， 以(i，j，LCL，L，λ，d)值为输入，计算相应的转移概率值pij;

Step4 利用Minitab的拆分列“Unstack”、列转置“Transpose”，以及数据复制“Copy”功能，将列变量存储为转移概率矩阵R；

Step5 计算ARL值，利用Minitab的“Diagonal”产生单位矩阵，“Subtract”矩阵运算，“Invert”矩阵求逆，“Multiply”矩阵乘积等宏命令；

Step6 (反馈机制)记录不同的偏移系数δ、状态空间划分k，控制限L，平滑系数λ下的ARL计算结果，分组拟合ARL与k，λ值的关系曲线，从中筛选出符合要求的优化参数设置.具体，根据EWMA控制图检测中小偏移为主的特征，设置偏移系数δ=0，δ=1，分别拟合出ARL与(k，λ)的等值线图(图2)； ARL与k的关系曲线图(图3)；ARL与λ的关系曲线图(图4).以上图形都是用Minitab作图功能绘制.

(k，λ)组合对ARL的影响是综合性的：δ=0时，不同控制限制L的设置下，ARL取值随着λ取值的变化，始终呈现“梯度”特征，且在平滑系数λ取值较低的阶段，ARL均较长.这样的结果说明了过程受控时，若平滑系数λ取值较低(0.1附近)，EWMA控制图可以减少“误报”(图2).

δ=1时， ARL取值随着λ取值的变化虽然仍呈现“梯度”特征，但在不同控制限制L的设置下，ARL与平滑系数λ取值的变化并没有呈现相似的变化趋势.L=3，平滑系数λ取值较低区间[0.1，0.4]，ARL较短；L=2，平滑系数λ取值落在[0.4，0.6]区间，ARL较短.这样的结果说明了过程非受控时， EWMA控制图可以尽早“报警”，但需要将控制限和平滑系数进行动态的调整(图2).

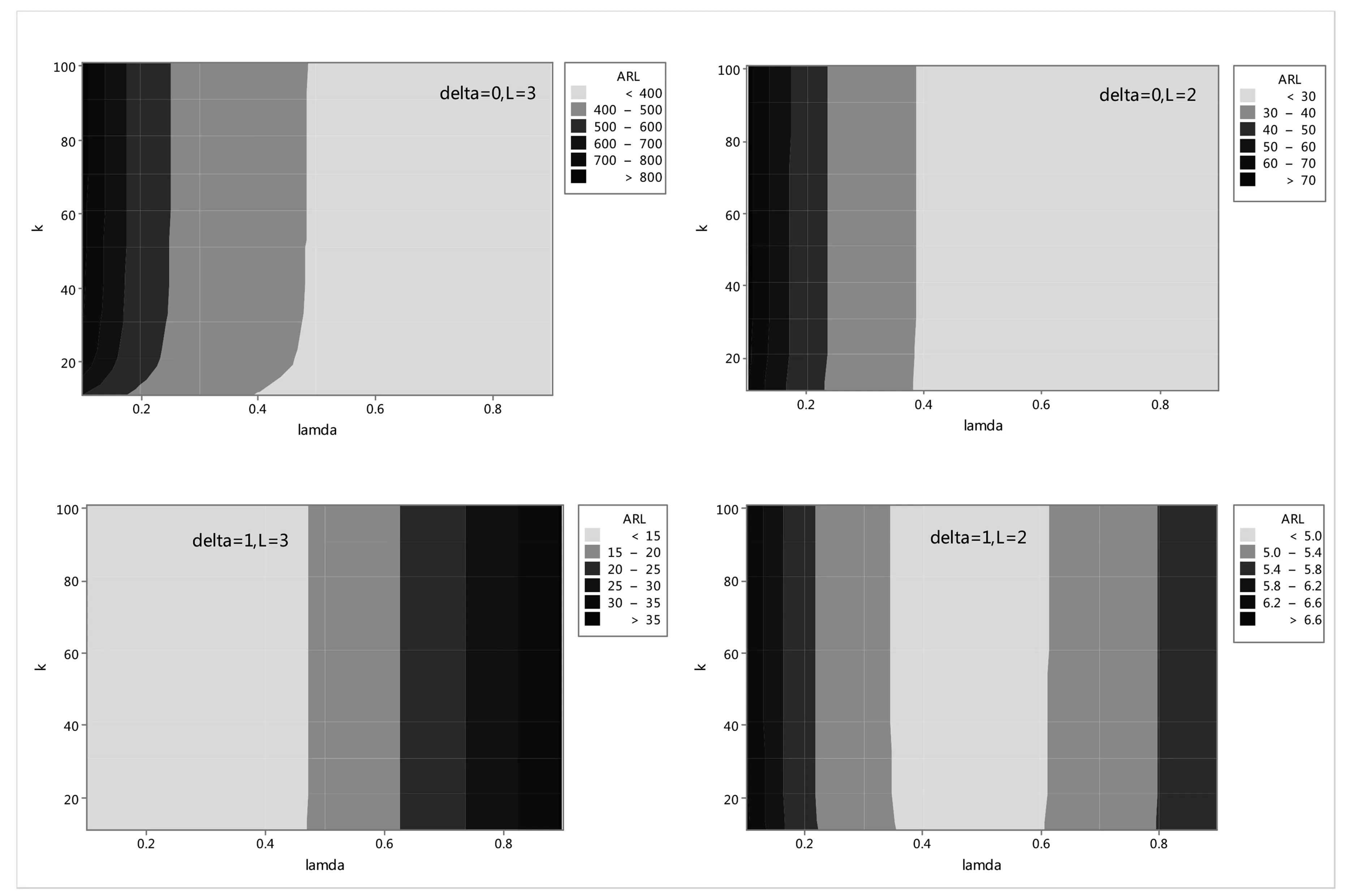
图2 控制图受控、失控时，ARL与(k，λ)的等值线图

固定(k，λ)中的一个，ARL与另一参数间的关系则更加特征鲜明：

δ=0时，不同控制限制L的设置下，ARL受状态空间k的影响较小，仅仅在平滑系数λ取值较低(0.1)时，出现一定的影响作用(图3(a)); δ=1时，不同控制限制L的设置下，ARL受状态空间划分k的影响均较小(图3(b)).

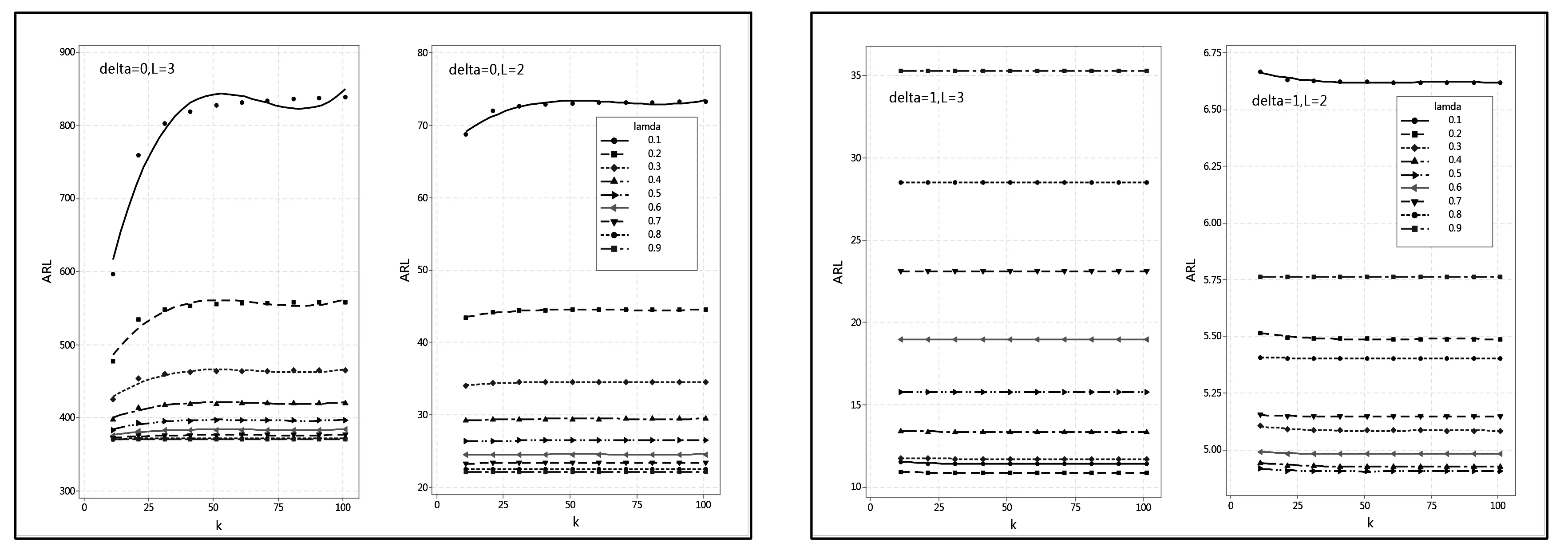
(a) 受控时，ARL与k的关系拟合图 (b) 非受控时，ARL与k的关系拟合图图3 ARL与k的关系拟合图

δ=0时，不同控制限制L的设置下，ARL受平滑系数λ设置的影响较大，和等值线图显示的结果一致，平滑系数λ取值较低(0.1)时，ARL均较长(图4(a)).

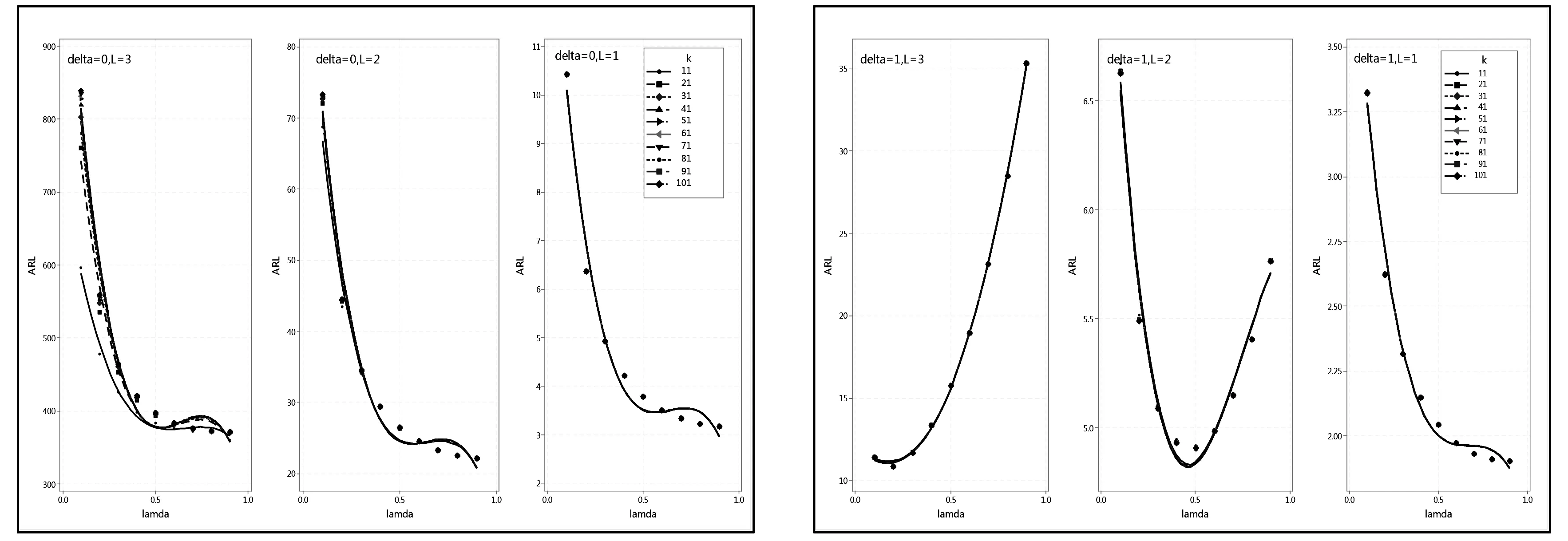
(a) 受控时，ARL与λ的关系拟合图 (b) 非受控时，ARL与λ的关系拟合图图4 ARL与λ的关系拟合图

δ=1时，不同控制限制L的设置下，ARL随着平滑系数λ的取值不同，呈现差异化的变化趋势：控制限较大，ARL随着λ的取值变大而变长；控制限中等，则ARL随着λ的取值变大而先变短后又变长；控制限较小时，ARL随着λ的取值变大而变短(图4(b)).

综合以上仿真分析结果，遵循控制图优化的基本原理，受控时，EWMA控制图应选取较小的平滑系数值；而当过程非受控时，应结合控制限L的宽度，相应的平滑系数值也要作出变化：L宽，则λ小；L中等，则λ中等；L窄，则λ大.这样的取值关系，可以使得受控时的ARL较长，非受控时ARL较短，实现控制图优化的目标.

3 结 论

本文以统计软件Minitab为基础，设计了一类统计学专业实践教学中的拓展案例.该案例以质量控制领域的控制图优化理论为基础，结合Minitab的数据处理特征、功能模块以及宏命令语言，实现了控制图的仿真优化.该案例完整、高效的实现过程说明，功能性统计软件在高校统计学专业实践教学中具有非常大的潜力，这类软件的教学推广，是对广泛流行的SAS、SPSS、R以及Stata等主流统计软件的有益补充.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.