半函数线性模型的k近邻经验似然推断
2021-07-09凌能祥
汪 文, 凌能祥
(合肥工业大学 数学学院,合肥230601)
1 引 言
在过去的二十年中,函数型数据分析(FDA)受到了广泛的研究,并成为统计研究中最重要的领域之一.文献[1]首次将函数型数据引入到线性模型中.为了更好的拟合效果,文献[2]首次引入了半函数部分线性回归(SFPLR)模型
其中Xj(j=1,2,…,p)是解释变量,βT=(β1,β2,…,βp)是一列未知参数,利用核方法构造了参数分量和非参数的估计值,并给出了参数分量的渐近正态性和非参数分量的收敛速度.文献[3]进一步考虑了在响应变量随机缺失时相关分量的研究结果,并给出了实验模拟和真实数据分析.文献[4]利用k近邻方法研究了SFPLR模型.文献[5-6]提出了在参数置信域构造上优于正态逼近的经验似然方法.文献[7]分别将经验似然方法应用于响应变量缺失下的半函数线性模型和SFPLR模型.文献[9]和文献[10]分别利用k近邻进行时间序列分析,和研究函数型数据.本文利用经验似然方法研究了SFPLR模型,通过k近邻方法构造了模型中参数分量的经验似然比统计量,并得出该统计量具有渐近χ2分布,并同时给出了非参数分量的估计值及其收敛速度.
2 估计方法
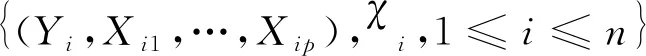
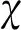
(1)
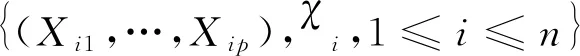
定义权函数
令
且
的kNN估计分别是
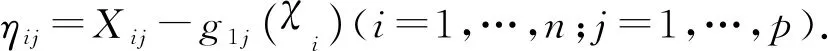
显然E[Zi(β)]=0.利用此信息定义β的经验对数似然比函数为
利用Lagrange乘子法,可得
其中λ(β)为Lagrange乘子,满足
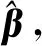
3 定 理
定义空间SH上 Kolmogorov’sε-熵为ψSH(ε)=log(Nε(SH)),其中Nε(SH)为在空间H上必须覆盖SH的开球半径ε的最小值.并给出以下具体假设:
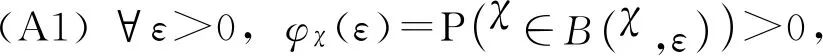
(A2) 存在函数φ(·)≥0,f(·)>0,对α>0,常数τ>0,有
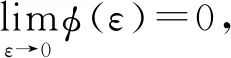
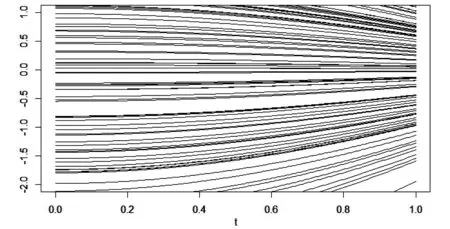
(ii) ∃C>0,η0>0,对∀0<η<η0,φ′(η) (iv) ∃C<∞使得∀(u,v)∈SF×SF, ∀f∈{m,g11,…,g1p}, |f(u)-f(v)|≤Cd(u,v)α; (A3) 核函数K(·)满足: (i)K(u)是非增函数且在支集[0,1)上Lipschitz连续, (ii) 若K(1)=0,则-∞ (A4)SH的 Kolmogorov’sε-熵满足: (A5)k=kn是正实数序列且满足: 注 文献[9]中的定理2在证明本文的渐近结果中起到了重要作用,因此需要假设条件(A1)-(A5),具体原因见文献[9],(A6)是研究SFPLR模型的常见条件[2]. 定理1假设(A1)-(A6)成立,如果n→∞时,有 Iα(β)={β∈Rp|-2R(β)≤Cα}. 定理3在定理1的条件下 有 证具体的证明过程见文献[3]. 引理2假设定理1中的条件成立,若β是参数的真值,那么 (2) 据文献[4]的(7.7-7.8)和(7.15-7.16)有 根据文献[4]的(7.9)-(7.11),得到 根据以上对公式(2)的分解,可以得到 由于ε与(X,χ)相互独立,根据引理1可得 引理4在定理1的条件下,若β是参数的真值 证具体的证明过程分别见文献[6]中的引理3和文献[5]中的定理1. 定理1的证明令 根据引理4可得 根据引理2和引理3 其中‖·‖代表欧几里得范数,由文献[9]的定理1和定理2可得证明成立. 图1 曲线i(t),i=1,…,100,t∈[0,1] 核函数 表1 β的95%置信区间覆盖率 分析 经验似然方法能取得很不错的实验结果,即获得比较大的置信区间覆盖率.随着样本量的增加和误差的减小都会使置信区间覆盖率增大. SFPLR模型综合了参数回归和非参数回归模型的特点,具有更大的适用性,而经验似然方法在构造置信域方面有许多突出的优点.本文创新性的用kNN方法取代了N-W核方法,解决了用经验似然方法处理SFPLR模型的问题,分别给出了关于参数和非参数部分的估计值和渐近正态性.之后利用所得结果构造参数的置信域,并通过模拟研究说明了经验似然方法在参数的覆盖概率大小上表现优异. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.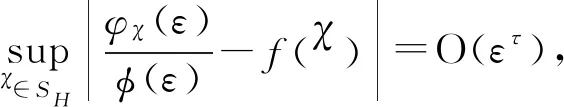
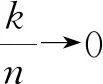
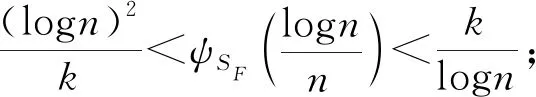
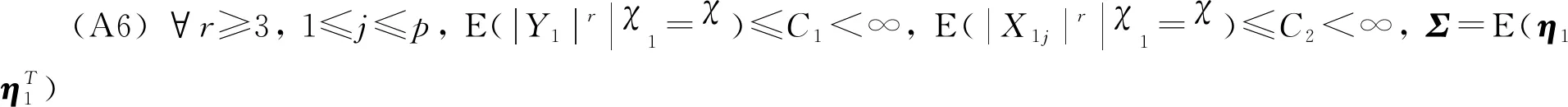
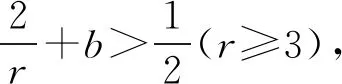
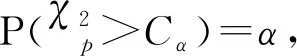
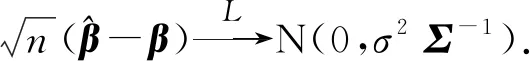
4 定理证明
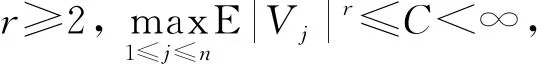
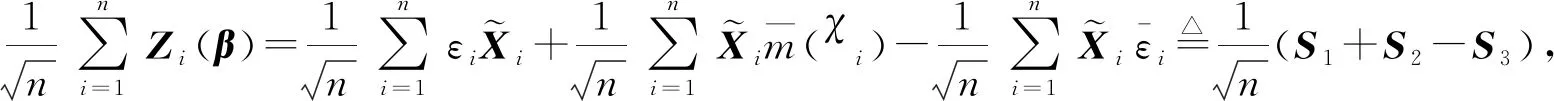
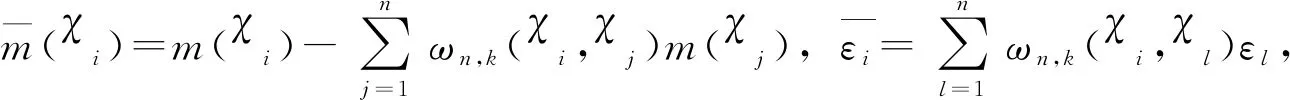
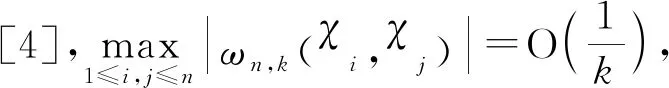
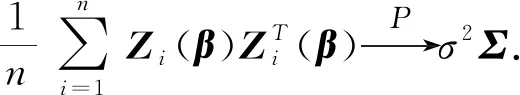
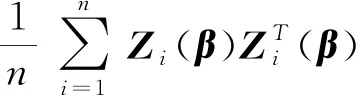
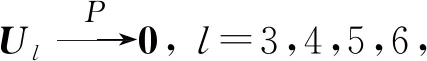
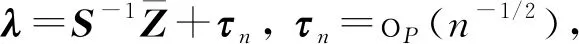
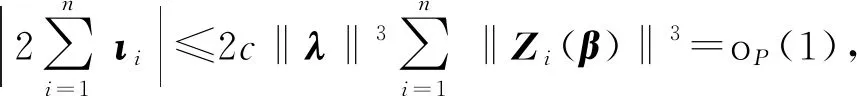
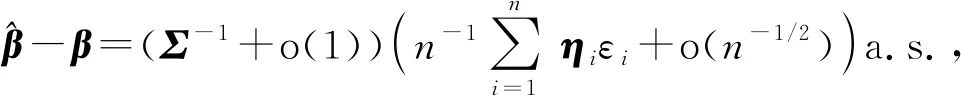
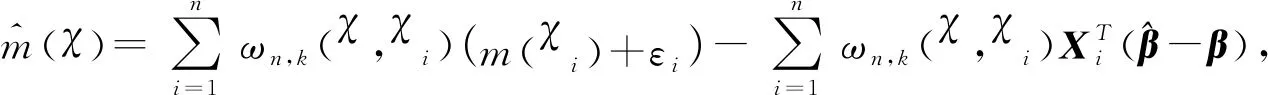
5 模拟研究
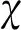
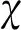
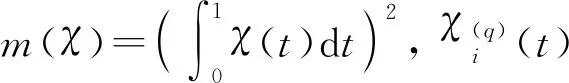
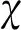

6 结 论
