工业CT三维图像的表面平滑方法

王佳熙

(成都大学 计算机学院，四川 成都 610106)

0 引 言

工业CT(computed tomography，CT)技术能够在不破坏工业部件的前提下得到具有复杂结构工业部件的三维图像.但受检测环境或设备自身等因素的影响，其获得的测量数据在采集和传输过程中会受到噪声的干扰，进而影响到经图像重建后得到的工业部件的三维图像质量.与一般的检测方式不同，工业CT技术获得的并不是工业部件表面的点云数据，而是被扫描工业部件的三维图像灰度体数据，其需要通过图像分割或其他的方法才能得到工业部件的三维图像表面.但是，这些方法都会带来一些伪影，比如图像表面出现毛刺或部分不连续的情况，这会使三维图像表面的网格模型的三角面片数目过多，进而影响后续的逆向设计和改造等图像后处理过程.针对以上问题，科研人员进行了相关研究并取得了一定进展[1-6].针对噪声问题，刘玲慧等[1]提出了三维鲁棒Chan-Vese(3-dimension robust chan-Vese,3D-RCV)算法，其通过在3D-CV算法的基础上引入局部灰度信息来解决工业CT三维图像中存在的噪声问题.其研究表明，3D-RCV算法能较好地获得用水平集函数表示的工业部件的三维图像表面.而针对图像的平滑方法，Buades等[5]提出了非局部均值算法，其把图像中出现的很多周期性冗余信息加以利用，在全局中搜索灰度相似块并充分利用像素之间的相关性，从而更好地保护图像的边缘特征.董斌等[6]提出了基于水平集的非局部表面恢复算法，其利用水平集函数来表示三维图像表面，从而使得三维图像的表面在边界得到保护的同时减少了大量的噪声，而且在表面有毛刺和部分不连续的地方进行了重造，图像整体变得更为平滑.在此基础上，本研究针对工业CT三维图像所含噪声过多而导致得到的工业部件三维图像表面有毛刺和部分不连续的缺点，将3D-RCV算法和基于水平集的非局部恢复算法结合用于工业部件三维图像的表面平滑.同时，通过网上公开的工业部件的灰度体数据测试了算法的可行性与有效性.

1 工业CT三维图像表面平滑方法

本研究探讨的工业CT三维图像的表面平滑方法大致可分为两个步骤：其一，利用3D-RCV算法对工业部件的三维图像灰度体数据进行三维分割，获得用水平集函数φ表示的工业部件的三维图像表面；其二，采用基于水平集的非局部表面恢复算法对获得的结果进行三维图像表面平滑处理.

1.1 3D-RCV算法

3D-RCV算法的主要思路是：对于图像中的每一个像素点，它与其邻域内的所有像素点的灰度信息都具有一定的相关性.例如，图像中某个像素点x，在它的邻域内一定存在没有被噪声污染的像素点.即使有些点被噪声污染，仍然可以利用它的邻域内没被噪声污染的像素点的信息来帮助曲面进行相对正确的演化，这样就不会被噪声点完全影响而导致错误的演化.

1.1.1 模型建立

设I：Ω→R是图像域Ω⊂R3上的一幅灰度图像，Ω1和Ω2是Ω被一个二维曲面C划分成的两个互不相交的同质子区域，即，Ω=Ω1∪C∪Ω2，Ω1∩Ω2=φ.给定图像中的一个点x(x,y,z)∈Ωi,i=1,2，定义该点的局部能量如下,

(1)

式中，常数ci是子区域Ωi的平均灰度，I(y)是点x的邻域N(x)内的像素点y(x,y,z)的灰度值，邻域N(x)的大小通过核函数Kσ来控制.这里，选取截断的高斯核函数作为Kσ，定义如下，

(2)

式中，σ是高斯函数的标准差，a是正则化常数，邻域N(x)的半径记为r.

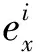
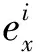
x,y∈Ω

(3)

式中，λ1>0,λ2>0,为固定的参数.

下面引入面积正则项，则该算法的总体能量定义为，

F(C,c1,c2)

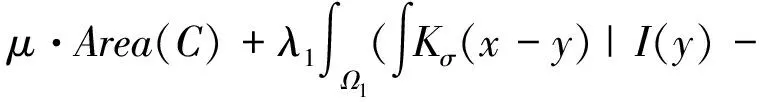
c2|2dy)dx,x,y∈Ω

(4)

在水平集方法中，演化曲面C⊂Ω可以用Lipschitz函数φ：Ω→R(也称为水平集函数)的零水平集来表示，具体形式如下,

(5)

按文献[7]的变分水平集表示方法，分别定义正则化Heaviside函数Hε(z)和Dirac函数δε(z)如下，

(6)

(7)

为了保持水平集函数的光滑性，使用文献[8]定义的水平集函数正则项P，

(8)

1.1.2 模型求解

综上，总体能量F(C,c1,c2)可以被改写成如下形式，

Fε(φ,c1,c2)

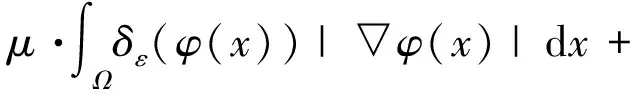
|I(y)-c2|2dy)(1-Hε(φ(x)))dx,

x,y∈Ω

(9)

式中，μ≥0,ν≥0,分别是面积项和水平集正则项的参数.

该方程可以采用变量交替迭代和梯度下降的方法进行求解.由此，使得总体能量最小化的各个变量的解析表达式如下：

首先，固定ci,i=1,2，Fε(φ,c1,c2)对水平集函数φ的导数可以转化为如下梯度下降流方程，

ν·div(dp(|▽φ|)▽φ)

(10)

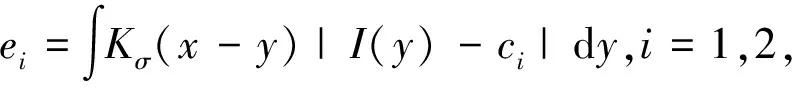
然后，固定水平集函数φ，令泛函F(φ,c)对ci求导，可得到使函数F(φ,c)最小时的ci解析式为,

(11)

式中，Mi(φ(x))定义为，

(12)

1.2 基于水平集的非局部表面恢复算法

1.2.1 模型建立

近年来，图像平滑算法已延拓到了三维图像的表面平滑，其主要采取两种方式来表示三维图像的表面：其一是用三角形网格；其二是用比较隐式的方式，比如水平集函数.后者的优点是数值计算简单与拓扑结构灵活多变.而拓扑结构的灵活多变是很重要的，它不仅能去噪，还能进行拓扑修正[8].

非局部均值方法是Buades等[5]提出来的，其主要用来对图像进行去噪，具体过程为，

NL(u)(x)

(13)

式中，c(x)是一个标准化因子.

da(u(x),u(y))

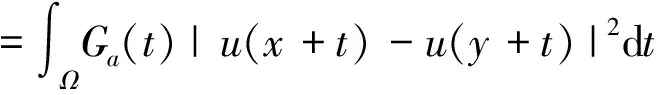
(14)

式中，Ga是一个标准偏差为a的高斯函数，用非局部均值来对图像进行去噪可以得到较好的效果，其能量函数[6]可以写成，

(15)

该函数对应的梯度下降流是一个非局部热方程，

ut=Δωu：

(16)

式中，x∈Ω.

式(16)经过有限差分法可得到其离散版本，

(17)

式中,uj表示u在网格点j处的值，j取遍计算域的所有的网格点.Nj是网格点j的邻域使得当l∈Nj时候，ω(l,j)>0.CFL限制条件使得dt满足,

(18)

1.2.2 模型求解

基于水平集的非局部表面的恢复算法具体步骤如下：

(1)用水平集函数φ来表示图像的表面，

(19)

式中，∑表示一个区域，S表示该区域的边界.

(2)把φ的0水平集附近的一个狭窄的区域记作∑η，η是该区域的宽度.

(3)计算权重ω(x,y)和相似函数D(x,y)，

(20)

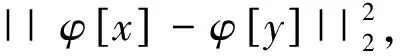
x∈∑η,y∈Nx

(21)

式中,Nx是∑η中x的邻域，φ[x]是φ以x为中心处的3D块.

(4)对能量函数J(u)的梯度下降流使用有限差分法得到其离散的迭代格式如下，

(22)

式中，ωjl可以由上式计算得出，令dt为,

(23)

式中，j遍历完∑η中所有的网格点.

(5)设置算法的迭代次数k.

2 结果与分析

为了测试本研究所提出方法的可行性，利用网上公开的工业部件的灰度体数据进行相关测试实验.软件平台为,MATLAB_R2016b分析工具.硬件平台为,组装台式机，其主要配置为,Inter(R)Core(TM)i5-6500 CPU@3.20 GHz，8 GB内存，64位Windows操作系统.

2.1 参数选取

本研究的方法中存在一些参数，而参数的选取会影响实验的结果，故需要先对这些参数进行分析和讨论.

首先，在3D-RCV算法中，参数λ1、λ2和水平集正则项参数ν在实验中可以设置为λ1=λ2=1,ν=1，而面积项参数μ则需要根据待分割图像的不同类型进行调整.面积项参数调整的规则是：当μ取得比较小的时候可以分割出图像中的细小物体；如果需要分割出较大的目标，μ就应取得相对大一点.另外，算法中高斯窗口的半径大小的选取对分割结果也有一定的影响，它的选取主要和噪声的强弱有关.根据经验来说，如果图像中的噪声较大，高斯窗口的半径就应取得大一些，反之亦然.在实验中，高斯窗口选取的半径为7×7×7.

其次，基于水平集的非局部表面恢复算法中，参数b1是两个网格点之间距离的惩罚权重，b2是两个3D块之间的惩罚相似性权重.b1比较大的时候，更能利用远处的信息；而b2比较大时候，更能保护尖锐的特征.本研究根据经验选取，b1为1 000，b2为600，区域的宽度η选择为2.因为图像所含的噪声种类不同，难以找到一个统一的停止准则，所以算法的停止迭代步数通常根据经验选取，本次实验选取停止迭代步数为300步.

2.2 结果与分析

实验中，本研究通过网上公开的发动机的灰度体数据来测试方法的可行性.

首先，利用3D-RCV算法对发动机的灰度体数据进行三维分割得到用水平集函数表示的工业部件的三维图像表面，结果如图1(a)所示.然后，采用基于水平集的非局部表面恢复算法对其进行平滑处理，结果如图1(b)所示.

从图1(a)可以看出，经过3D-RCV算法分割后得到的发动机的三维图像表面有很多毛刺和部分不连续的地方.由图1(b)可以看出，而经过基于水平集的非局部表面恢复算法平滑处理后，发动机的三维图像表面在边界得到保护的同时减少了大量的噪声，在表面有毛刺和部分不连续的地方还进行了重造，图像整体变得更加平滑.

(a)3D-RCV分割后的图像

下面再从图1中选取2个局部区域进行放大来具体说明上述结论.

图2是图1中用箭头①所示矩形框标出来的左下部分的局部放大图.图2(a)中的图像表面凹凸不平，整体非常的不光滑，而经过平滑处理后，图像的表面整体变得非常平滑(见图2(b)).

(a)3D-RCV分割后的图像

图3是图1中用箭头②所示矩形框标出来的右下部分的局部放大图.图3(a)中图像存在有毛刺和部分不连续的地方，经过平滑处理后，其在边界的大体形状得到保护的同时，还进行了重造，图像整体变得更为平滑(见图3(b)).

(a)3D-RCV分割后的图像

3 结 论

针对工业CT图像所含噪声过多而导致所得到的工业部件三维图像表面有毛刺和部分不连续的情况，本研究将3D-RCV算法和基于水平集的非局部表面恢复算法相结合用于工业部件三维图像的表面平滑处理.实验测试结果表明，经过本方法平滑处理后的工业部件的三维图像表面在边界得到保护的同时减少了大量的噪声，而且在表面有毛刺和部分不连续的地方进行了重造，图像整体变得更为平滑.本研究为工业CT三维图像的可视化软件的逆向设计和改造提供了高质量的三维图像，减少了后期处理的计算量和存储量.