由一道竞赛题看直角坐标与自然坐标的选取技巧

李洪全 李 燕

(1. 成都树德中学，四川 成都 610000； 2. 雅安职业技术学院，四川 雅安 625000)

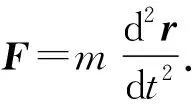
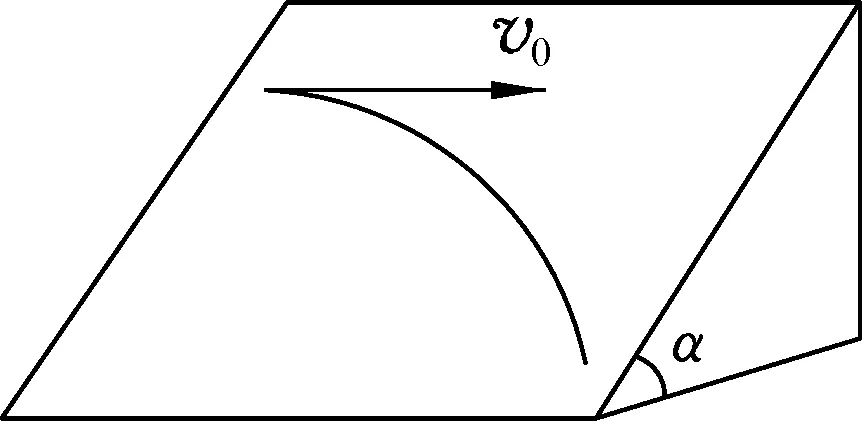
图1

例题.一质量为m的物体放在斜面上，斜面的倾角为α，如图1所示，物体与斜面间的动摩擦因数μ恰好满足μ=tanα，今使物体获得一水平速度v0而滑动．

1 解法1：建立直角坐标系求解

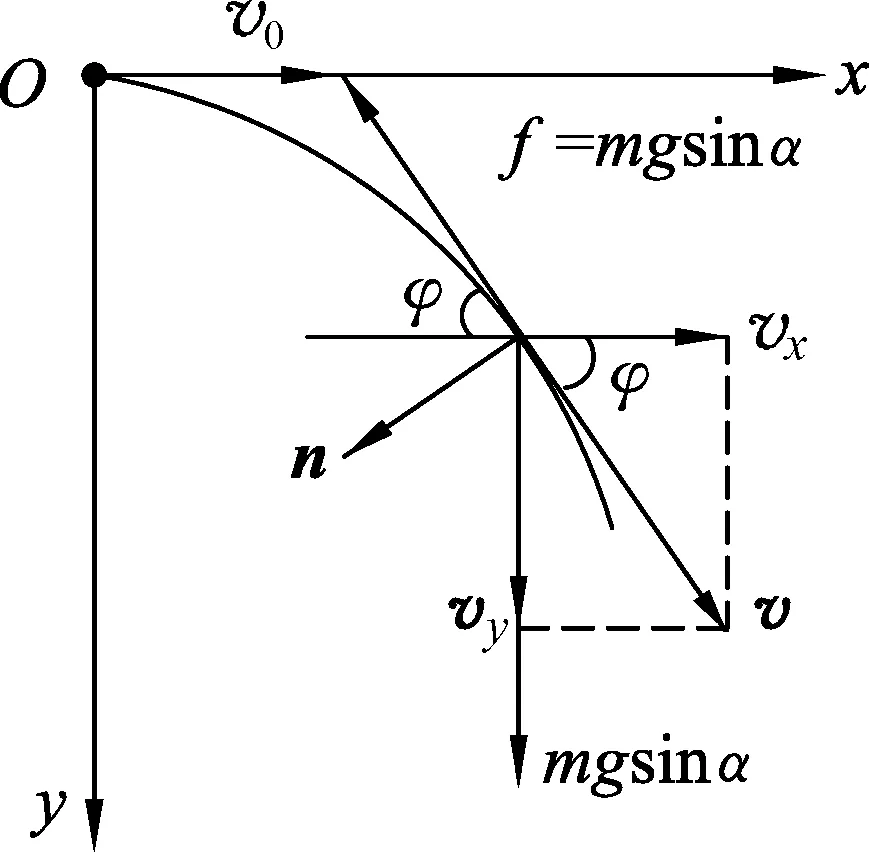
图2

物体所受力有重力G，弹力N以及摩擦力f．重力分解为沿平行于斜面与垂直于斜面的分量G1和G2，G1=mgsinα，G2=mgcosα．垂直于斜面方向物体平衡，有G2+N=0，即N=mgcosα．

f=μN=μmgcosα=mgtanαcosα=mgsinα.

在Oxy坐标系中，列动力学微分方程如下.

x方向：

(1)

y方向：

(2)

(3)

(4)

因为vx=vcosφ，vy=vsinφ，故由(3)、(4)式得

-gsinαcosφ·dt=d(vcosφ).

(5)

gsinα(1-sinφ)·dt=d(vsinφ).

(6)

(5)式除以(6)式得

(7)

由(7)式得

vcos2φdφ+sinφcosφdv=

vsinφ(1-sinφ)dφ+cosφ(sinφ-1)dv.

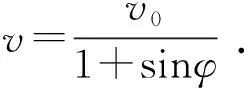
2 解法2： 建立自然坐标系求解

自然坐标系表示法：在已知的质点运动轨迹上，选定任意一点为原点O，用由原点至质点位置的弧长作为质点的位置坐标，一般取沿曲线切线且指向自然坐标增加的方向为切向单位矢量τ；另取沿曲线法线且指向曲线的凹侧为法向单位矢量n，如图3所示．把这种顺着已知的质点运动轨迹建立的坐标系称为自然坐标系．

图3

(8)

法向方向：

(9)

(9)式中ρ表示曲线在该点的曲率半径．

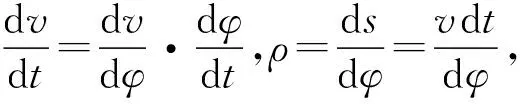
(10)

由式(8)-(10)得

(11)

由(11)式写出积分

(12)

积分可得

(13)

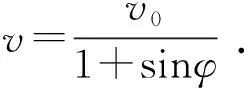
点评：解法2中使用自然坐标，在法向和切向两个参考方向列动力学微分方程，但求解时需要细致写出曲率半径的微元表达式，要注意几何关系，相比解法1运算量有所下降．

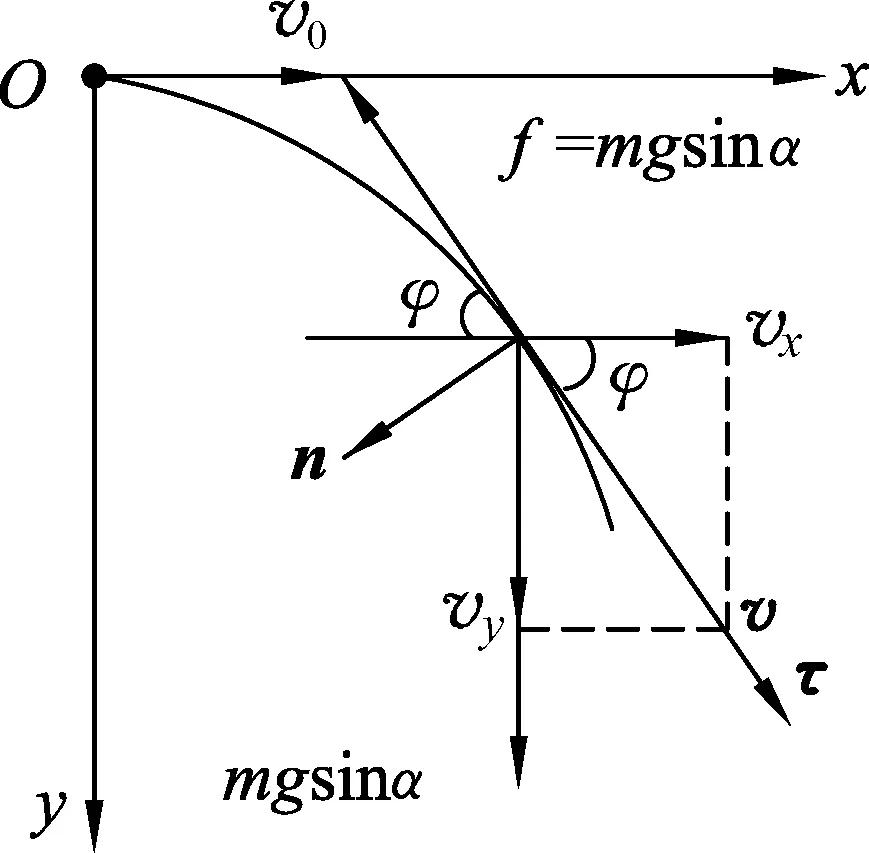
图5

3 解法3：自然坐标系和直角坐标系联合使用求解

y方向：

gsinα(sinφ-1)dt=dv，

gsinα(1-sinφ)dt=dvy.

d(v+vy)=0.

(14)

对式(14)积分得v+vy=v0，因为vy=vsinφ，故有v+vsinφ=v0.

点评：解法3，直角坐标和自然坐标联合使用，在切向与沿斜面向下这两个方向列动力学微分方程，相比解法1和解法2，运算量减小，解答过程最为简便．