一类非线性微分方程的超越整函数解

韦燕红，徐俊峰

（五邑大学 数学与计算科学学院，广东 江门 529020）

1 引言与定理

本文使用Nevanlinna理论的符号，假设读者熟悉值分布的相关理论（详见参考文献[1-2]）.

设f(z)是复平面C上的亚纯函数，如果非恒为零的亚纯函数a(z)满足T(r,a)=S(r,f)（这里S(r,f)=o(T(r,f))(r→∞)，除了关于r的一个可能存在的有限例外集），则称a(z)是f(z)的小函数.

定义1设f是非常数亚纯函数，aj(j=0,1,2,…,n)是f的小函数且都不恒为零，Mj(j=0,1,2,…,n)皆为f的系数为1的微分单项式，称P(f)=a0M0(f)+a1M1(f)+…+anMn(f)为f的微分多项式.

定义2设f是非常数亚纯函数，aj(j=0,1,2,…,n)是关于z的多项式且都不恒为零，称为f的代数微分多项式.其中，I是多指标有限集，|γ|:=i0+…+in称为P(z,f,f',…,f(t))对应每一项的次数.

在研究复微分方程理论的众多问题中，证明给定微分方程的整函数或者亚纯函数解的存在性和给出解的形式，一直是一个有趣且相当困难的问题，特别是非线性微分方程.大量学者运用Nevanlinna值分布理论，研究了一系列非线性微分方程[3-6].其中，文献[5]得到了如下结果：

定理1设n≥3是一个整数，P(f)表示f(z)的次数不超过n-3的代数微分多项式，b(z)是亚纯函数，λ,c1,c2是 3个不 为零 的常 数，那么 微分 方程fn(z)+P(f)=b(z)(c1eλz+c2e-λz)没有 满足T(r,b)=S(r,f)的超越整函数解.

文献[6]进一步研究非线性微分方程：

其中，p1(z) ,p2(z)是2个不为零的多项式，α1,α2是2个非零常数且α1/α2不是有理数. 如果n≥4，P(f)是f(z)的次数不超过n-3的代数微分多项式，则方程（1）没有超越整函数解.

文献[6]推断P(f)的次数不超过n-2或n-1时，上述结论也成立.

2016年，Zhang等[7]考虑用fnf'取代方程（1）的主要部分fn，研究非线性微分方程：fnf'+其中，Qd(z,f)是以有理函数为系数的微分多项式，p1,p2是f的小函数，α1(z),α2(z)是非零整函数. 2017年，陆小庆[8]考虑用fnf(k)取代方程（1）的fnf'来研究非线性微分方程：

其中，Qd(z,f)是以f的小函数为系数的微分多项式，p1,p2是f的小函数，α1(z) ,α2(z)是非零整函数.

在2020年，Xue[9]考虑方程右边有3个指数型的非线性微分方程：

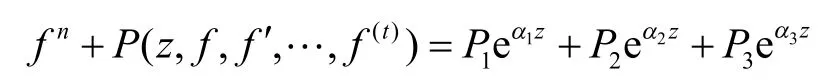
在|α1|＞|α2|＞|α3|下的超越整函数解的形式，得到了以下定理.

定理2[9]设n≥2是一个整数，t是整数，P(z,f,f',…,f(t))是次数不超过n-1的代数微分多项式.其中，Pi和αi是非零常数，对于i=1,2,3，有|α1|＞|α2|＞|α3|.如果f(z)是方程

的超越整函数解，那么f(z)=a1eα1z/n，这里a1是满足a1n=P1的非零常数，对于i=1,2,3，αi是线性的.

注1事实上，定理2的证明过程只在n≥3时成立.

受文献[7-9]的启发，本文考虑用fnf(k)取代方程（3）中的fn，得到如下定理：

定理3设n≥3，k≥1是整数，t是整数，P(z,f,f',…,f(t))是次数不超过n的代数微分多项式.其中，Pi和αi是非零常数，对于i=1,2,3，有|α1|＞|α2|＞|α3|.如果函数f(z)是方程

下面给出3个例子进行说明.

例1函数f(z)=ez是f4f''+f3f'+f'=e5z+e4z+ez的超越整函数解，其中，f3f'+f'的次数是4次，这说明方程的解是存在的.

例2函数f(z)=ez-1=是的超越整函数解，其中，的次数是4次.此时，这说明代数微分多项式不超过n这一条件是精确的.

例3函数f(z)=ez是f3f'+f2(f'')2+f2f'+ff'=2 e4z+e3z+e2z的超越整函数解，其中，n=3,k=1,P1=2,α1=4，f2(f'')2+f2f'+ff'的次数是4次.这说明代数微分多项式不超过n这一条件是精确的.

注2函数f(z)=ez是方程f2f'+ff'+f'=e3z+e2z+ez的超越整函数解，其中ff'+f'的次数是2次.由此，我们猜测定理3在n=2时也成立.

2 引理

证明定理3需要下述引理以及其证明.

引理1[2]设fj(z)(j=1,2,…,n)(n≥2)为亚纯函数，gj(z)(j=1,2,…,n)为整函数，且它们满足下列条件：

3）当1≤j≤n且1≤h＜k≤n时，其中，E⊂(1,∞)是有限线性测度或对数测度集），那么，fj≡0(j=1,2,…,n).

引理 2设n≥ 1,k≥ 1 均是整数，α,c是非零常数，f是方程fnf(k)=ceαz的超越整函数解，那么f(z)=c1eαz/(n+1).其中c1是非零常数且c1n+1=c(n+1)k/αk.

证明因为则f(z)=其中u(z)是f(z)的小函数.

由fnf(k)=ceαz知f(z)无零点，故u(z)是非零常数.因此，f(z)=c1eαz/(n+1)，其中c1是非零常数.

引理3设n,m,k是3个整数且n≥m≥ 2，k≥1，αi(i=1,2,…,m)是互不相同的非零常数.那么

没有超越整函数解，其中Pj(j=1,…,m)是非零常数.

证明设f(z)是方程（5）的超越整函数解.一方面，即

另一方面，

综上得，f(z)的级为1.

若f(z)无零点，则可设f(z)=ceαz，其中α,c为非零常数.将f(z)=ceαz代入式（5）得：

又αi(i=1,2,…,m)是互不相同的非零常数，c,α是非零常数.因此，当αi=(n+1)α时，有：

根据引理1，得：

这与Pi(i=1,2,…,m)是非零常数矛盾.因此f(z)有零点.

令g(z)=fnf(k)，z0是f(z)的q阶零点，此时q＞k.否则，f(k)=0.方程（5）可写作：

又αi(i=1,2,…,m)是互不相同的非零常数，所以由引理1有，Pi=0(i=1,2,…,m)，这与Pi(i=1,2,…,m)是非零常数矛盾，所以q＞k.此时在z的邻域内解析.那么0且ψ(z0)≠ 0，这里ψ(z)是解析函数.因此，

显然z=z是g(z)的nq+q-k阶零点.故有于0是有：

显然，这是齐次线性方程组.上述方程组的系数矩阵为

因为n≥m,q≥ 1,k≥1，所以nq+q-k-1 ≥m-1.m-1个方程的系数矩阵行列式为：

因为αj(j=1,…,m)互不相同，所以|A|≠0，与已知矛盾.因此，引理3得证.

引理4[9]如果P(z,f,f',…,f(t))是f(z)的次数为d的代数微分多项式，α是非零常数.那么，αP(z,f,f',…,f(t))-P'(z,f,f',…,f(t))也是f(z)的次数为d的代数微分多项式.

3 定理3的证明

设f(z)是方程（5）的超越整函数解，令F1(z)=fnf(k)，Q1(z)=P(z,f,f',…,f(t))，则方程（5）可写成：

方程（6）两边同时微分，得：

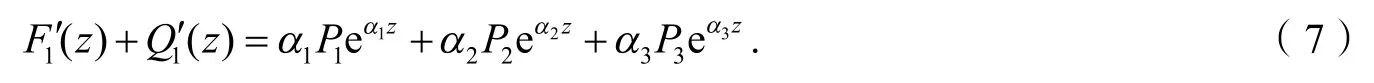
由方程（6）和（7）消去eα1z，得到：

取F2(z)=F1'(z)-α1F1(z)，Q2(z)=Q1'(z)-α1Q1(z)，则方程（8）可写作：

以下分4种情形讨论式（9）.

情形1F2(z)≡0 和Q2(z)≡0，这是不可能的，因为αj是互不相同的常数.

情形2F2(z)不恒等于0，Q2(z)≡0，有：

其中1A是非零常数.由式（6）和（10）得：

根据引理3有，当n≥3时，方程（5）没有超越整函数解.

情形3F2(z)≡0,Q2(z)不恒等于0，有其中C1是非零常数.结合引理1有：

其中γ≤d,d是微分多项式P(z,f,…,f(t))的次数.

由式（6）（11）和（12）有：

因为γ/n＜1，所以

其中，γ1=d或γ2=d.显然，是方程（4）的超越整函数解.

情形4F2（z）,Q2（z）均不恒等于0，对方程（9）微分后，得：

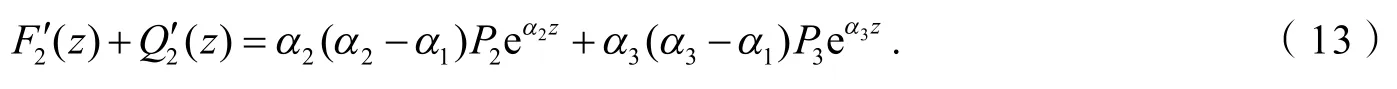
由式（9）和（13）消去eα2z，有：

取F3(z)=F2'(z)-α2F2(z)，Q3(z)=Q2'(z)-α2Q2(z)，则方程（14）可写成：

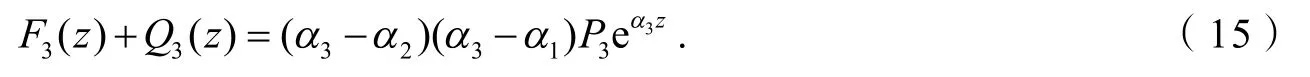
和上面证明类似，对式（15）也分为4种情况进行讨论.

情形4.1F3(z)≡0 和Q3(z)≡0是不可能的，因为αj是互不相同的常数.

情形4.2F3(z)不恒等于0，Q3(z)≡0，有Q2(z)=A2eα2z，其中A2是非零常数.又Q2(z)=Q1'(z)-这里A1,A2是非零常数.因此有：

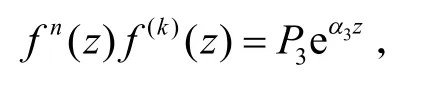
和

此时γ≤d.与|α1|＞|α2|＞|α3|矛盾.

情形4.3F3(z)≡0，Q3(z)不恒等于0，有：

其中C2是非零常数.类似地，有这里C1,C2是非零常数.根据引理3，得出矛盾.

情形4.4F3(z),Q3(z)均不恒等于0，那么方程（15）微分后，得：

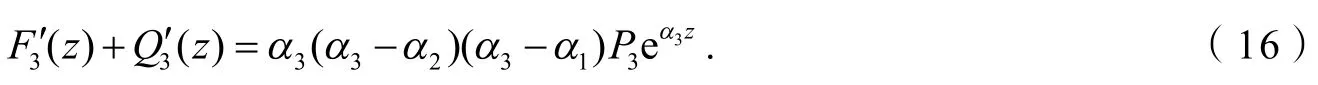
由式（15）和（16）消去eα3z，有：

即

根据引理4，得知F3'(z)-α3F3(z)的次数是n+1，但是-α3Q3(z)的次数d≤n.因而只有当F3'(z)-α3F3(z)=Q3'(z)-α3Q3(z)=0 成立时，方程（17）才能成立.

由F3'(z)-α3F3(z)=0，即

这里A1,A2,A3是非零常数.根据引理3，此时方程没有超越整函数解.