利用移动主成分分析识别结构损伤

李 欣 郭恩国

(1.广州市启韵房地产开发有限公司，广东 广州 510770； 2.广州建设工程质量安全检测中心有限公司，广东 广州 510440)

0 引言

桥梁作为基础设施的重要组成部分，承担着经济发展和生活质量的重要作用。为了及时掌握桥梁运营情况，保证桥梁在服役期间安全可靠的运营，有必要建立完善的监测系统对桥梁状态进行实时监测。结构健康监测(SHM)系统已广泛应用于大型民用基础设施中，根据安装在结构上的传感器在结构使用寿命期间的反馈信息，对结构状态进行实时监测[1]。

结构健康监测所面临的主要问题之一便是从获取的海量数据中提取有用信息，以此来评估桥梁结构状态。马宏伟提出应发展利用少量传感器信息及基于大数据与人工智能的安全监测新方法，来克服现有系统传感器繁多、造价昂贵、海量数据难以处理的问题[2]。利用数据驱动的方法进行实时在线监测桥梁结构运营状态受到了广泛学者的关注[3-5]。

1 移动主成分分析(MPCA)

1.1 移动主成分分析流程

主成分分析(PCA)广泛应用在结构损伤识别中，可以降低数据维数、消除环境影响、提取损伤特征等[6-9]。移动主成分分析(MPCA)本质上是在主成分分析基础上添加恒定大小的移动窗口，将PCA应用于恒定大小的移动窗口数据，而非整个数据集，既让PCA能够应用于连续时间序列数据，同时又减少了计算时间。Posenato等人[10]提出移动主成分分析(MPCA)算法，用于连续监测结构异常状态。

假设从安装在结构上所有传感器采集的时间序列组成数据矩阵Ut，如下所示：

其中，s为传感器数量；n为时间序列的观测总数，矩阵的列向量表示传感器所采集的时程响应数据。

选择合适的移动窗口，将恒定大小的移动窗口随着时间沿矩阵Ut移动，计算每次移动窗口内的主成分，第k次移动后，移动窗口内的数据可表示为：

其中，k=1,2,3,…,(n-w)为窗口移动的次数;w为移动窗口的长度。对窗口内的数据进行标准化处理，第j次观测数据标准化后的向量为：

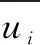
通过特征值分解，求解协方差矩阵的特征值和特征向量。

(Ck-λiI)Ψi=0 (i=1,2,…,s)。

特征向量Ψi即为主成分，按特征值贡献率进行降序排列。MPCA识别结构损伤最关键的问题是选择窗口大小和窗口移动间隔[11]。移动窗口的大小通常是时间序列周期的倍数；窗口移动间隔应考虑重叠的数据不会对窗口数据产生影响，论文选择和窗口大小相同的长度作为移动间隔。

1.2 损伤时刻的确定

结构损伤会导致结构特性的变化，这些变化隐藏在动力响应信号中，主成分分析可以从响应信号中识别模态参数[12]。前几阶主成分包含了时间序列的大部分方差，当损伤发生时，响应信号的特征向量和特征值也会发生变化，因此可以分析响应信号的主成分来反映结构是否发生损伤。将主成分分析应用于移动窗口，动力响应时间序列便转化为特征向量时间序列。选择第一阶主成分和对应特征值作为损伤指标[13]，连续监测窗口内损伤指标的变化，如果在某时刻，损伤指标发生了突变，就表明在这一时刻，桥梁结构特性发生了变化，结构出现了异常状态。

2 简支梁模型数值模拟

2.1 数值模拟参数

采用有限元软件ANSYS建立简支梁数值模型，数值模型如图1所示。采用Plane42单元，材质为钢材，截面为矩形，截面尺寸为0.1 m×0.2 m，密度为7 850 kg/m3，弹性模量为210 GPa，泊松比为0.3，全梁长20 m。沿简支梁长度方向上均匀布置9个传感器采集加速度信号，在3号传感器处施加随机荷载，荷载大小范围为-1 000 N～1 000 N，采样频率为200 Hz，采样时间为5 s。

在4号传感器处通过删除单元格模拟不同程度的损伤。设置4种不同程度的损伤工况，损伤宽度均为0.04 m，损伤程度分别为梁高的2/15，3/15，4/15和6/15。

2.2 数值模型结果分析

数值模拟工况包括完好结构和损伤工况共5种工况，每种工况各进行10次模拟实验，每次模拟实验提取9列加速度信号。为了模拟连续监测桥梁的情形，同时满足MPCA数据量的计算要求，分别从完好结构状态和不同损伤结构状态的响应数据中各随机抽取250组数据进行拼接，沿着拼接后的数据计算窗口内的第一阶主成分和对应特征值。在时间序列上来说，拼接后的数据前1 250 s的时间序列是健康数据，后1 250 s的时间序列是损伤数据。通过损伤指标的变化来监测结构的运营状态，识别结果如图2～图5所示。

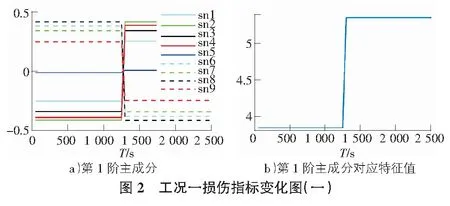
数值模拟结果表明，在四种不同损伤工况下，动力响应信号的损伤指标均在1 250 s时刻发生了突变，表明结构在1 250 s时刻出现了异常情况。结构未发生损伤前，时间序列的损伤指标随着时间平稳地变化，当结构受到损伤时，损伤指标发生突变，结构受到损伤之后，损伤指标又随着时间平稳地变化，这是因为结构的自适应性调整其自身特性，结构内力重新分配组合，以新的容许能力进行运营，因而损伤后时间序列的损伤指标也会变得平稳。

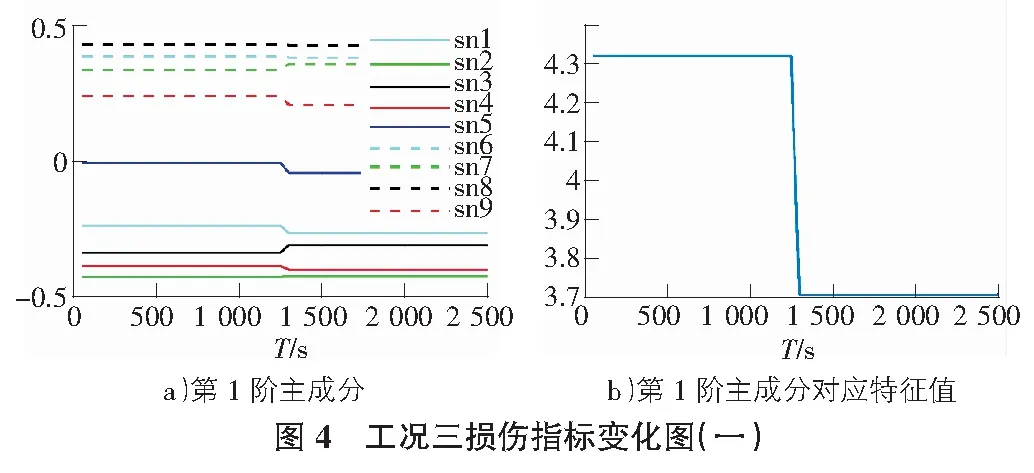
为了进一步说明MPCA识别损伤发生时刻的能力，将5种工况的时间序列信号依次拼接进行MPCA，模拟实时监测桥梁运营。以4号传感器时间序列的损伤指标为例，结果如图6所示。

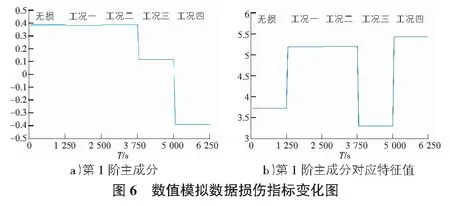
由图6可以明显看出，依次对所拼接的时间序列进行MPCA分析时，不论结构损伤程度大小，一旦结构特性发生改变，时间序列的第一阶主成分和对应特征值均会出现突变，准确识别出损伤发生时刻，监测出结构异常状态。

3 简支梁模型实验

3.1 实验方案

简支梁实验模型采用钢板条，长度为1.2 m，横截面尺寸为1 cm×3 cm。同样在3测点处施加随机荷载，荷载大小通过调节电压进行变化，本次实验选用的电压为0.2 V。在4单元处设置损伤，沿梁横向对称切割设置不同深度的损伤工况，损伤宽度均为1.5 mm，损伤工况深度分别为3 mm，6 mm，9 mm和12 mm。布置好的实验模型如图7所示。

每种工况分别进行10次实验，共采集50组实验数据，包括10组完好结构的时间序列数据以及40组不同损伤工况的时间序列数据。实验的采样频率为2 048 Hz，采样时间为8 s，每次实验采集的加速度数据矩阵维数为9列，2 048×8行。实验数据中选择5倍的采样频率作为移动窗口的长度。

3.2 实验结果分析

同样地将完好数据分别与不同损伤工况数据进行拼接，随机选取250组完好结构的加速度数据，分别与250组不同损伤程度结构的加速度数据进行拼接，每种工况共组成500组数据集。根据采样频率转换到时间域上，即完好结构的加速度数据总共有2 000 s，损伤结构的加速度数据总共有200 s，500组数据集的时间长度共4 000 s。利用MPCA连续计算时间序列的损伤指标。识别结果见图8～图11。

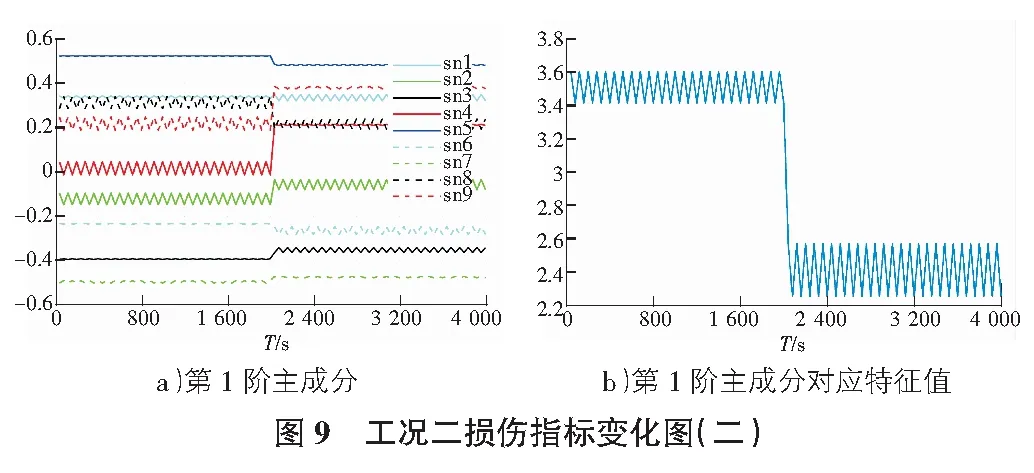
由实验数据结果表明，在四种不同损伤工况下，时间序列数据的损伤指标均在2 000 s时刻发生了突变，准确识别出了损伤时刻。损伤指标突变量并不是随着结构损伤程度的增加而增加，因此，MPCA并不能评估结构的损伤程度。此外，特征值的突变量要远大于主成分的突变量，表明时间序列的特征值对损伤的敏感性比其对应的特征向量要高，同时特征值的维数要远小于特征向量的维数，将特征值作为损伤指标进行监测又进一步降低了数据维数。

同样将实验数据中完好结构与四种不同损伤结构的时间序列依次进行拼接，利用MPCA沿时间序列计算其损伤指标，结果如图12所示。

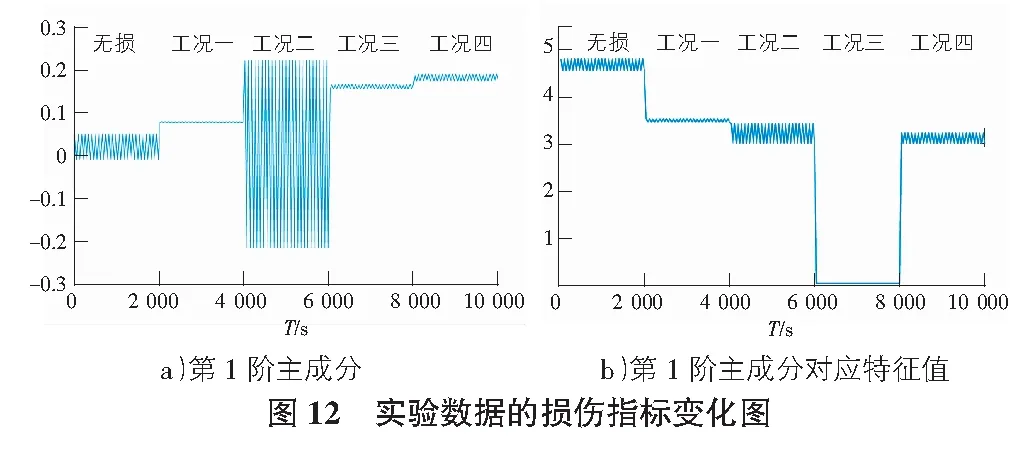
由图12可知，时间序列的损伤指标均在不同损伤发生时刻出现突变，MPCA准确识别出结构不同损伤发生时刻。从实验结果还可以看出，工况2的损伤指标变化量远大于其他工况，在线弹性系统中，由于施加的是随机荷载，激振力大小会影响结构的动力响应信号幅值，导致其时间序列的损伤指标发生变化。因此，在随机荷载作用下使用MPCA监测桥梁运营状态时，须保证随机荷载的幅值在一定范围内变化。实验数据结果表明，MPCA能够准确识别损伤时刻，连续实时监测桥梁结构运营状态，为工程实际应用提供了可行性实践。

4 结语

准确识别桥梁结构损伤发生时刻对结构健康监测具有重要意义，可以为桥梁管理维护提供预警信息，并及时采取相关措施。MPCA因其强大的降维能力，可以连续监测结构的实时状态，并显示出良好的识别效果。通过研究可以得到如下结论：

1)MPCA作为一种无模型数据解释的算法，在结构健康监测中，不依赖结构类型和模型参数。其强大的降维能力同时又能提取主要损伤特征，解决了实时监测中海量数据难以处理的问题。

2)利用MPCA可以识别结构损伤发生时刻，连续监测桥梁结构运营状态，但无法评估损伤程度。

3)MPCA可以应用在动力响应信号数据中识别结构损伤。研究表明，时间序列协方差的第一阶特征值和对应特征向量均能识别结构损伤发生时刻，但特征值对损伤的敏感性比其特征向量更高，同时特征值的维数更低，因此可以选择时间序列的第一阶特征值作为损伤指标，既能降低数据维数又能监测结构的特性变化。