轨道随机不平顺的谱表示-随机函数模拟及应用

刘付山，曾志平,2，王卫东,2

(1.中南大学 土木工程学院，湖南 长沙 410075；2.中南大学 重载铁路工程结构教育部重点实验室，湖南 长沙 410075)

轨道随机不平顺是由不同波长、不同幅值、不同相位的不同不平顺波叠加而成的随线路里程变化的复杂随机过程[1]。轨道随机不平顺常通过线路实地测量获得，并采用功率谱密度函数表示其统计特征，我国及英国、日本、德国等都测定了各自的轨道不平顺谱密度和相关函数。然而，在非线性车辆-轨道耦合系统中，功率谱密度函数无法直接输入动力系统，最有效的办法是以轨道随机不平顺的时域样本作为输入。翟婉明等[2]提出一种根据轨道随机不平顺功率谱求出频谱的幅值和随机相位，再通过傅里叶逆变换得到轨道随机不平顺时域样本的数值模拟方法。除此以外，三角级数法也是采用较多的一种轨道随机不平顺时域样本数值模拟方法[3]。众所周知，随机分析计算效率随着所需样本数增加而增加，为了更加高效的研究轨道随机不平顺激励下的车辆-轨道耦合系统随机振动特性，需要用更少的随机样本来反映轨道随机不平顺的统计特性。无论是常用的三角级数法还是傅里叶逆变换法，在模拟轨道随机不平顺时都需要大量的随机变量，而分析所需的随机样本数与随机变量数正相关。因而用更少的随机变量来描述轨道随机不平顺，可极大提高的车辆-轨道耦合系统随机振动分析的效率及难度。

文献[4]中，通过随机谐和函数法生成轨道随机不平顺时域样本，并通过频率与相位分别随机以减少所需的随机变量数，其中随机频率数为50个，考虑轨道高低、方向、水平、轨距不平顺情况下，各种不平顺相互独立，随机频率和随机相位共计需400个随机变量，所需随机变量依然很多，且单个随机样本中频率分量减少必然会导致模拟的轨道不平顺与实际偏差增大，并不能很好地反映不平顺的时域特征，该方法可用于线性车辆-轨道耦合系统中轨道随机不平顺的模拟，但不适用于非线性车辆-轨道耦合动力学系统。

本文基于谱表示方法，将谱表示方法中的标准正交随机变量表达为基本随机变量的正交函数形式，从而实现用较少随机变量来描述轨道随机不平顺的目的。减少随机变量数的同时，保留更多的频率及相位分量，可更准确反映轨道随机不平顺统计特性以及时域特征，提高非线性车辆-轨道耦合系统随机振动计算效率。

1 随机过程的谱表示-随机函数模拟

一维、单变量、功率谱密度函数为S(ω)的随机过程η(t)可以表示为[5]

(1)

式中：Ut(ω)和Vt(ω)为随机过程η(t)的谱过程，其增量dUt(ω)和dVt(ω)满足随机过程谱表示的基本条件，即

其中，E[·]表示数学期望；ω、ω′为随机过程中的频率；S(·)为双边功率谱密度函数。

对式(1)进行离散，并引入一组标准正交随机变量{Xk,Yk}，当频率间隔Δω足够小时，式(1)可表述为

(2)

式中：dUt(ω)≈ΔUt(ω)=σkXk; dVt(ω)≈ΔVt(ω)=σkYk;σk=[2S(ωk)Δω]1/2，S为轨道不平顺功率谱密度函数；Nω为频率离散点数；频率分量均匀离散情况下，ωk=ωl+k·Δω，Δω=(ωu-ωl)/Nω，ωu、ωl为频率离散点上、下限值。

(3)

式中：cas(x)=cos(x)+sin(x)为Hartley正交基函数；随机变量Θ1、Θ2相互独立且服从区间[0，2π)上均匀分布。直接生成的标准正交变量并不能直接代入式(2)，还需要构造随机映射将标准正交变量映射到标准正交随机变量{Xk,Yk}，由此将描述随机过程的随机变量数降低为2。

2 轨道随机不平顺的谱表示-随机函数模拟方法

以TB/T 3352—2014《高速铁路无砟轨道不平顺谱》[6]为例，轨道不平顺谱包括高低、方向、轨距和水平四种轨道不平顺谱，计算不平顺谱时，将实测得到的轨道不平顺按1 024 m划分单元，剔除异常值和趋势项，加窗处理后进行傅里叶变换(FFT)计算，对所有单元的轨道不平顺谱进行拟合，得到轨道不平顺功率谱密度函数。我国的轨道不平顺谱拟合公式为

(4)

式中：f为空间频率；A、k为拟合系数。

统计误差可表示为

(5)

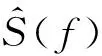
需要指出的是，轨道不平顺功率谱密度函数是在大量实测数据基础上，按一定单元长度组成轨道不平顺样本集，由样本集计算得到的均值谱。单个轨道不平顺分段的随机误差达到了100%，随着分段次数的增加随机误差逐渐减小，如果分段100次则随机误差可以降到10%[6]。因而采用单个轨道随机不平顺样本或单元计算得到的不平顺功率谱与现有轨道不平顺功率谱对比，并不能说明数值模拟方法的准确性，需采用多个不平顺样本或分段所组成的样本集不平顺功率谱与现有轨道不平顺功率谱对比验证。

对于多样本模拟，常采用蒙特卡罗法选择随机变量，但其计算效率偏低。拟蒙特卡罗法是通过数论方法产生高度均匀化的拟随机数序列代替蒙特卡罗随机数模拟，以减少随机样本数从而提高计算效率，但当随机变量较多，即高维度情况下，数论选点法选取的随机数列不可避免的会产生丛聚现象[7]。采用谱表示-随机函数法模拟生成轨道不平顺时域样本，可减少所需的随机变量数，避免高维数论选点中丛聚现象对计算结果的影响。

综上所述，采用谱表示-随机函数法生成轨道随机不平顺样本集过程可表示为

Step1根据生成的轨道随机不平顺类型确定随机变量数N，当需同时生成轨道高低、方向、轨距、水平不平顺时，由于各类型不平顺间相互独立，因而需要8个随机变量(各类型不平顺均为2个)。

Step2根据所需随机变量数，采用拟蒙特卡罗法生成随机变量的低偏差序列Θ，常用的低偏差序列有Corput序列、Halton序列、Sobol序列等[7]。本文采用Sobol序列生成随机变量[5],采用Matlab直接计算Sobol的命令。

Θ={θ1j,θ2j,…,θNj}j=1,2,…,Npt

式中：N为随机变量数；Npt为样本集合的样本数。此时生成的随机变量序列服从[0,1)上均匀分布, 需将其变换为[0，2π)上均匀分布随机变量Θ′

Θ′=2πΘ

(6)

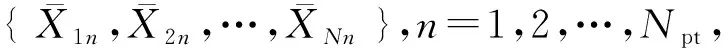
高低不平顺ηV(t)为

方向不平顺ηA(t)为

水平不平顺ηC(t)为

轨距不平顺ηG(t)为

式中：SV、SA、SC、SG分别为高低、方向、水平、轨距不平顺功率谱密度：ωk为轨道随机不平顺中不同的频率分量，其表达式为

(7)

采用谱表示-随机函数模拟方法生成样本数为300的轨道随机不平顺样本集，其中轨道不平顺功率谱计算方法中单元长1 024 m，采样间隔0.25 m，单个单元共计4 096个点，因而模拟轨道随机不平顺时频率离散点数Nω取4 096。

对生成的轨道不平顺样本集中各样本，参考文献[8]中高速铁路无砟轨道不平顺谱的生成方法及轨道不平顺谱频率分布规律检验方法，采用周期图法计算得到各样本的不平顺谱值，并求得样本集不平顺谱均值，对各频点不平顺谱值Sk,j按下式进行变换

(8)

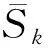
采用Kolmogorov-Smirnov检验方法，对λk,j进行显著性水平α=0.05、自由度为2的χ2分布检验。轨道不平顺单样本情况、单样本功率谱、样本均值、样本标准差、部分频点功率谱概率分布CDF等评价指标以及样本集总体功率谱PSD与目标谱对比情况如图1～图4所示。

图1 谱表示-随机函数法高低不平顺样本评价指标对比

图2 谱表示-随机函数法方向不平顺样本评价指标对比

图3 谱表示-随机函数法水平不平顺样本评价指标对比

图4 谱表示-随机函数法轨距不平顺样本评价指标对比

从图1～图4中可以看出，计算得到的轨道高低、方向、水平、轨距不平顺单个样本功率谱密度值与轨道不平顺功率谱存在较大的误差，而轨道不平顺样本集计算得到的功率谱均值与目标谱吻合较好，其中各种不平顺样本总体均值与目标谱最大相差分别为0.18、0.10、0.07、0.08 mm，标准差最大偏差分别为4.68%、5.77%、6.97%、6.99%，样本集功率谱最大偏差分别为14.54%、10.23%、10.07%、9.87%，各不平顺98.00%、96.33%、98.00%、98.33%的频点功率谱概率分布满足自由度为2的χ2分布。可以看出样本集各指标与目标谱吻合良好，且仅需8个随机变量便可同时模拟生成轨道高低、方向、水平、轨道不平顺时域样本，同时还具有大量频率分量。

3 轨道随机不平顺的数值模拟方法对比分析

目前在工程中应用较多的轨道随机不平顺数值模拟方法有三角级数和傅里叶逆变换法。三角级数法模拟轨道随机不平顺可表示为[2]

(9)

式中：ak为相互独立的均值为0、标准差为σk的高斯随机变数；φk为相互独立的随机相位。

傅里叶逆变换法模拟轨道随机不平顺可表示为[1]

η=ifft(X(k))

(10)

式中：X(k)为时间序列，其为复序列，实部关于Nr/2偶对称，虚部关于Nr/2奇对称。设模拟总时间为Ts，则时域采样点数为Ts/ΔT，一般需要在末尾添0以保证采样点数为2的整数次幂，即为Nr。

X(k)表达式为

k=0，1，…，Nr-1

(11)

式中：ξn为独立随机相位序列，ξn=cosφn+isinφn=exp(iφn)，φn服从[0,2π]上的均匀分布；Δf=1/(NrΔT)。

三角级数法中，ak为服从高斯分布的随机变量，φk为服从均匀分布的随机变量，因而三角级数模拟轨道随机不平顺时所需随机变量数为2Nω，且存在高斯分布与均匀分布的两种类型随机变量。傅里叶逆变化法中，仅有φn服从正态分布且相互独立，而所需随机变量数与时域采样点数相关，一般为2的整数次幂，当采样间隔0.25 m，模拟1 km轨道随机不平顺时所需随机变量数为4 096个。三种方法模拟轨道随机不平顺时域样本时，不平顺频率点计算方法基本一致，采用相同频率数时，具有相同的不平顺波长成分，因而文中仅对不平顺时域样本集的幅值进行对比分析。

采用拟蒙特卡罗法生成低偏差随机向量序列，通过三角级数法、傅里叶逆变换法模拟得到300个轨道随机不平顺时域样本。计算样本集均值、标准差、功率谱，并检验样本集各频点轨道谱分布，各项对比情况如图5和图6所示。各种方法生成的轨道不平顺样本集不平顺幅值范围情况见表1。

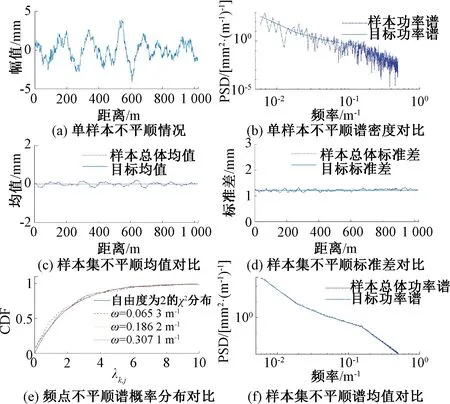
图5 三角级数法高低不平顺样本评价指标对比

图6 傅里叶逆变换法高低不平顺样本评价指标对比

表1 样本集不平顺幅值范围 mm

可以看出，除了傅里叶逆变换法计算得到高低不平顺幅值范围偏小外，三种方法计算得到的轨道随机不平顺幅值范围大体相当，最大相差5.51%。三角级数法计算得到的轨道不平顺单个样本功率谱与目标功率谱存在较大误差，各方向轨道不平顺样本集与目标谱均值最大相差分别为0.22、0.09、0.11、0.08 mm，标准差最大偏差分别为5.14%、6.78%、4.95%、7.25%，功率谱密度最大偏差分别为15.82%、13.93%、10.78%、9.65%，各不平顺97.33%、96.67%、97.33%、98.67%的频点功率谱概率分布均满足自由度为2的χ2分布。傅里叶逆变换法计算得到的轨道随机不平顺，无论是单样本还是样本集，其功率谱值均能很好满足目标功率谱，最大偏差仅分别为0.30%、0.24%、0.35%、0.13%，但各频点功率谱概率分布均不满足文献[8]中关于轨道不平顺谱分布的论述。除此以外，傅里叶逆变换法各方向轨道不平顺样本集与目标谱均值最大相差分别为0.28、0.11、0.13、0.07 mm，标准差最大偏差分别为11.38%、8.53%、8.73%、6.57%，与其他两种方法模拟结果基本一致。综上可以看出，谱表示-随机函数法在模拟轨道不平顺时域样本时其幅值范围基本一致。

4 非线性车辆-轨道-桥梁耦合系统随机振动分析

采用谱表示-随机函数方法仅需8个随机变量就可以描述四种轨道不平顺，这为非线性车辆-轨道-桥梁耦合系统随机振动提供了极大的方便。文献[9]中指出，由于涉及轮轨空间动态接触几何关系、轮轨切向蠕滑力和轮轨法向力等多种复杂非线性求解过程，车辆-轨道耦合系统最有效的随机振动研究方法是将轨道不平顺谱转换为时域样本，采用一段足够长的时域样本来代替整个随机过程，即采用蒙特卡洛法选取足够长的时域样本。

分别采用三角级数法、傅里叶逆变换法、谱表示-随机函数法模拟得到的轨道随机不平顺样本，利用三维非线性车辆-轨道-桥梁耦合动力学模型，计算得到系统动力响应，对不同距离上的动力响应结果进行统计分析，以轮重减载率、脱轨系数为例，样本计算结果截口概率分布PDF见图7。

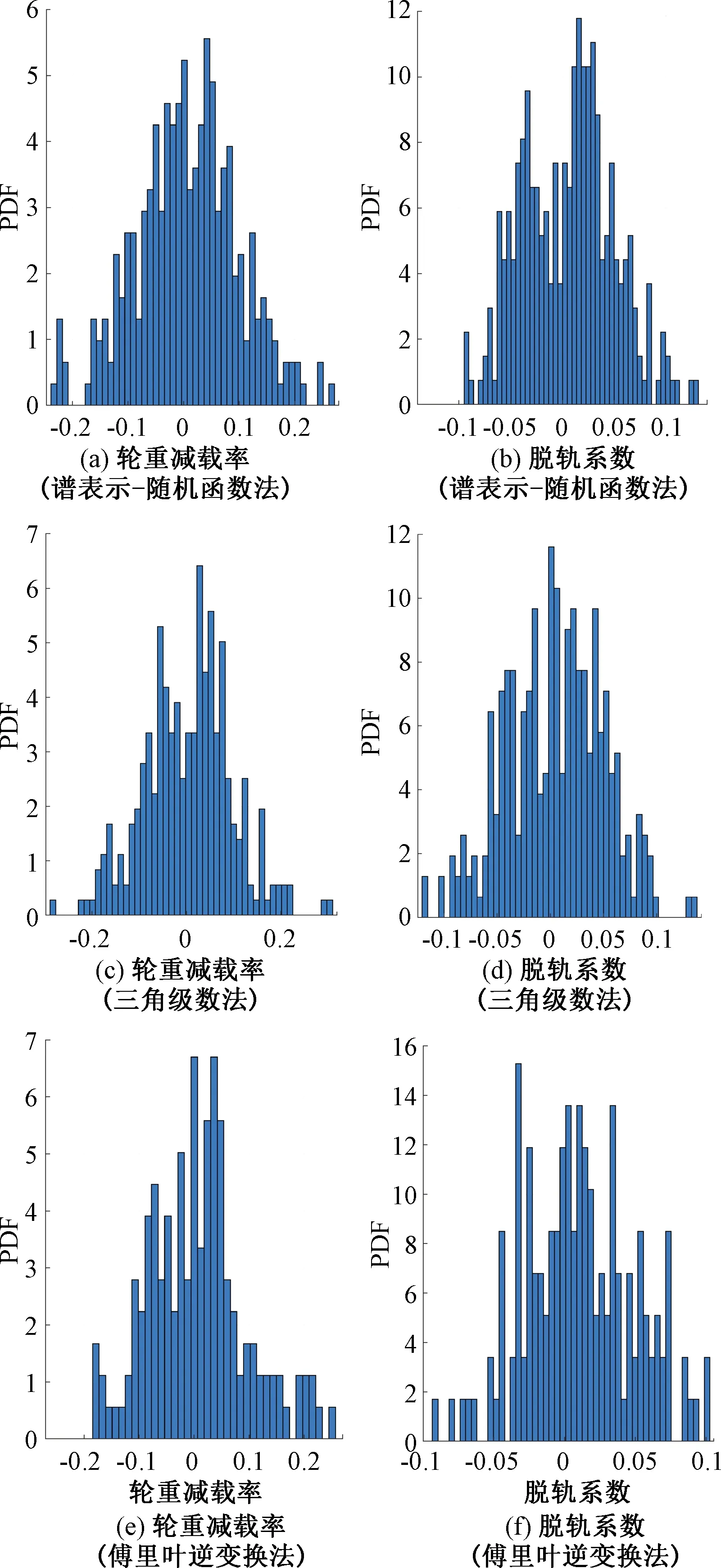
图7 不同计算法的响应截口概率分布

从图7中可以看出，在300个样本集的情况下，三种方法计算得到的动力响应其截口概率分布基本相同，都具有较大的离散性，速度300 km/h、不平顺波长2～120 m时，轮重减载率变化范围为±0.25，脱轨系数变化范围为±0.12。由于文中采用中国高速铁路无砟轨道谱，平顺性较其他轨道谱好，因而轮重减载率与脱轨系数的计算结果偏小。

对于车辆-轨道耦合系统动力响应，采用三种轨道不平顺谱数值模拟方法计算得到结果基本一致，但所需的随机变量数却存在巨大差异。随机变量数的减少方便了样本空间概率赋予，同时也可在一定程度上减少所需的样本数，为采用广义概率密度演化理论对车辆运行安全性进行评价提供了方便。

对于非线性车辆-轨道-桥梁耦合系统的任一动力响应ξ(t)，车辆运行过程中不考虑其他系统随机的情况下，其随机性来源于轨道随机不平顺中随机参数Θ的随机性，该系统为一个概率保守随机系统。根据随机系统的概率守恒原理，其应满足广义概率密度演化方程[10]

(12)

研究中常通过与大量蒙特卡洛法(MCM)计算结果对比，对广义概率密度演化方法(PDEM)计算结果进行验证[4,12]。采用三角级数法计算模拟轨道随机不平顺样本，结合MCM法计算得到3 000个样本动力响应统计情况，并采用谱表述随机函数法，结合广义概率密度演化理论，计算得到300个样本下的动力响应概率密度演化结果，两种方法车辆运行距离中间点的截口概率密度对比情况见图8，由于三角级数法所需的随机变量数较多，因而在3 000个样本情况下，动力响应结果依然存在一定离散性，但两种方法计算得到的截口概率密度基本一致，因而采用谱表示-随机函数法模拟轨道随机不平顺，结合广义概率密度演化理论可极大提高非线性车辆-轨道-桥梁耦合系统随机振动分析效率，相较于采用三角级数等方法模拟轨道随机不平顺并结合MCM法进行车辆-轨道-桥梁耦合系统随机振动分析，其计算效率至少可提高一个量级。参考“3σ”准则，取E±3σ对应值为动力响应指标最值。车辆运行过程中轮重减载率及脱轨系数最大值、等概率密度演化曲线见图9。由此，谱表示-随机函数法轨道不平顺数值模拟方法结合广义概率密度演化理论可对非线性车辆-轨道-桥梁耦合系统车辆运行安全性进行评价。

图8 MCM与PDEM截口概率密度对比

图9 等概率密度演化曲线

5 结论

轨道不平顺谱是描述轨道随机不平顺最常用的统计函数，本文以轨道随机不平顺时域样本数值模拟方法为研究对象，采用谱表示-随机函数法分别由2个随机变量模拟生成轨道高低、水平、方向、轨距不平顺集。

对比样本集与目标谱均值、标准差、轨道谱以及各频点轨道谱概率分布，验证了谱表示-随机函数法模拟轨道随机不平顺时域样本准确性；与三角级数法、傅里叶逆变化法相比，模拟生成轨道不平顺幅值范围基本一致，误差在5.51%以内，其中傅里叶逆变化法生成的不平顺样本功率谱能很好地吻合目标谱，但各频点功率谱分布并不满足与文献[8]所述频点功率谱分布；采用谱表示-随机函数法模拟生成轨道随机不平顺时域样本集，结合广义概率密度演化理论，可用相对较少样本计算得到车辆运行过程中概率演化情况，相较于采用三角级数法模拟轨道随机不平顺，并结合MCM法进行随机振动分析，计算效率至少提高了1个量级，为非线性车辆-轨道-基础结构耦合系统随机振动分析中轨道随机不平顺的模拟提供了新思路。