自适应参数与边缘点引导的深度图像超分辨
2021-07-09万文博祖兰晶薛泽颖王春兴
万文博, 祖兰晶, 薛泽颖, 王春兴
(1.山东师范大学 信息科学与工程学院,山东 济南 250358; 2.山东师范大学 物理与电子科学学院,山东 济南 250358)
0 引言
3D电影利用人的双眼视差,显示因位置差异而略有不同的2个图像,给观影者以身临其境的感觉。其中,3D场景的产生一方面主要依靠颜色数据,另一方面主要依靠高分辨率(high resolution,HR)深度数据。HR深度数据与颜色数据相比更难获得,因此成为研究的重点。
当前可通过利用彩色图像引导和深度学习等方式获得HR深度图。其中,Ren等[1]将图像中的像素点进行分类并将HR深度图像完成联合双边滤波(pixel category and joint bilateral filtering,PCJBF),该算法实验输出的任意像素点的深度值存在较大偏差。Gu等[2]提出加权分析模型,利用动态调整增强深度不连续区域,但不能有效利用彩色图像的引导作用。Yang等[3]提出用于HR深度修正的自适应彩色图像引导的自回归模型(autogressive model,AR),其即时性较差,所需的存储空间也较大,不能有效避免产生梯度反转伪像[4]以及细节边缘不清晰的问题。Qiao等[5]提出基于像素点聚类的深度上采样算法,当像素点所处区域的特性不同时,无法获得较好的像素点聚类与区域分割的结果。Ferstl等[6]利用图像建模优化,并使用各向异性扩散张量完成深度修正,不能降低不同区域间像素的影响。Wen等[7]利用卷积网络级联的深度学习算法完成图像超分辨,但GAN网络训练的稳定性不足,其结果不能充分地说明与解释其有效性。
针对上述问题,本文提出了自适应参数与边缘点引导的深度图像超分辨率重建算法。首先完成对LR(low resolution)深度图像的深度修正,保证其深度数据的准确性与有效性,并对像素点进行聚类;然后提出在用于HR深度图像重建的AR模型中加入多个自适应参数,可有效防止由彩色图像与深度图像结构差异引起的实验输出结果出现伪像的情况发生,同时降低处于不同区域像素间的影响,获得更精确的深度数值。
1 相关AR模型
Yang等[3]提出HR彩色图像引导的自回归模型完成深度图像超分辨。其中,AR模型如下所示:
(1)
(2)

Yang等[3]提出的AR模型在用于获得HR深度矩阵时,其获得的深度值不够准确,未考虑像素点处于不同区域的特性,忽略了像素点之间的强烈影响,不能合理有效利用HR彩色图,因此不能获得高质量的HR深度图像。
2 算法思路框架
2.1 LR深度图修正
由于LR深度图的深度可能会出现丢失、不准确等情况,本文提出的标记并修正不可靠像素点的算法,可以有效避免这种情况的发生,步骤如下所示。
对LR深度图使用Sobel算子获取边缘图SDL。对深度不可靠像素点进行标记:①深度值为0的点标记为不可靠像素点;②将图像分为3×3大小的不重叠的图像块,计算每个块内中心点与周围点像素值差值的绝对值,并记录绝对值大于3的个数, 如果个数大于t1,则将该区域的中心像素点标记为不可靠像素点,本文实验将t1设置为3;③如果图像块同时处于两个特性不同的区域,则利用SDL与边缘区域对比,同样对图像块中边缘处的像素点与区域临界处的像素点求其差值的绝对值,若绝对值大于3的个数超过t2,那么该像素点为不可靠像素点,t2在本文实验中设置为2。按照此种方法依次完成判断,标记出所有不可靠像素点。
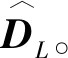
如图1所示,图1(a)和图1(c)表示未被预处理的LR深度图像,其中在边缘区域带有很多空洞,会对后期深度图像超分辨带来不利影响。图1(b)和图1(d)分别表示已完成LR深度修正的Books和Dolls图像,该图像深度信息完整,深度不连续区域得到增强,可有效完成后期深度图像的超分辨。

图1 LR深度修正图像Figure 1 LR depth repair image
2.2 改进AR模型系数
HR深度图D1是对LR深度图双三次插值的结果,但其存在一些问题,例如图像边缘模糊以及部分深度值误差较大。本文算法对AR模型进行改进,根据像素点的区域特性,通过加入一系列自适应参数,以预防出现梯度反转伪像以及由深度图与其对应的彩色图结构不一致而产生伪像的情况。对初始化深度图的深度不连续像素点采用深度修正,其公式如下所示:
(3)
(4)

2.2.1 深度项约束因子
在深度项中加入参数σd,x,其随像素点所处的3×3像素块变化,在同一个图像块设置相同的参数,可有利于均衡不同位置像素点的深度权值,使边界处像素点深度的差异度更平滑,促进两相邻像素间互相制约,确保深度的准确性。深度项约束因子的公式为
(5)
(6)

图2(a)和图2(d)分别表示Art、Laundry的彩色图像,图2(b)、2(c)和2(e)分别为图2(a)和2(d)的局部实验输出图像,其第1行与第2行分别表示参数σd,x随像素点自适应变化与随像素块自适应变化的局部实验输出图像。由图2可知,在图2(b)和图2(c)中,第1行图像的边缘区域出现部分缺失,第2行的图像边缘结构清晰且完整;在图2(e)中,第1行图像出现空洞是由于像素点所属区域特性的差异导致部分深度出现错误,因此参数σd,x随像素块自适应变化可确保深度不连续区域的完整性以及深度的有效性。

图2 实验结果图像对比Figure 2 Image comparison of experimental results
2.2.2 颜色项约束因子
在颜色项约束因子中,加入用于判断深度图与彩色图结构是否一致的参数τx,平滑参数σc,x与其相关,可根据像素点的区域特性改变彩色图像产生的权重。同时,加入用于降低处于不同区域边缘对侧像素点影响的控制参数εx,防止因区域特性的差异而导致深度上产生较大的误差。图3为颜色项约束因子算法的整体框架,其表达式为

图3 颜色项约束实现框架Figure 3 Implement framework for adaptive parameters of the color item
(7)
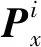
(8)
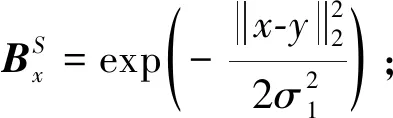
(9)
(10)

(11)
(12)
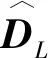
在图3中,用于调节彩色图像权重系数的常数σ5变为自适应变化的参数σc,x,这两种情况实验结果的比较如图4所示。其中,图4(b)、4(c)和4(e)的第1行为将σ5设为常数时图像局部区域的实验结果,第2行为参数σc,x随像素点自适应变化时的实验结果。第1行的图像存在部分锯齿以及模糊伪像的问题,第2行的图像更清晰,边缘细节丰富,可说明上述方法的有效性。

图4 算法输出图像Figure 4 The output images of the algorithm
3 实验结果与分析
为体现本文所提出算法的优势,采用深度数据集[8]中的深度与彩色图像对进行实验,本文列出Art、Books、Laundry等6幅图像的部分实验数据如表1所示。
通过表1可以看出,本文算法的实验输出图像都具有最低的BPR(坏点率),说明本文算法的性能较好,在AR模型中加入一系列自适应参数,可有效避免梯度反转伪像的产生,减小不同区域间像素点的影响,有效调节彩色图像的权重。

表1 实验输出结果的BPR比较Table 1 BPR comparison of experimental output results
图5提供了测试图像为Laundry、Moebius以及Reindeer,上采样因子为8时的实验结果图,其中,图5(a)为HR彩色图像,图5(b)为真实深度图像,图5(c)~5(g)分别表示TGV[6]、文献[2]、PCJBF[1]、AR[3]以及本文算法实验输出的高分辨率深度图像。对上述算法的实验结果进行主观视觉上的比较,从图5(c)和图5(d)可以看出,图像中空洞和伪像区域扩大;从图5(e)可以看出,图像增加了部分空洞区域;从图5(f)可以看出,细节边缘结构模糊,部分区域细节过于丰富;通过图5(g)可以看出,图像细节边缘结构清晰,整体清晰度较高。

图5 算法实验输出图像Figure 5 Algorithm experiment output image
图6为上采样因子为8的误差主观比较图像。误差主观比较图为真实深度图与不同HR深度图的差,线条越粗或越多反映了其误差越大,反之则说明其误差越小。图6(a)~6(f)为HR彩色图像以及TGV[6]、文献[2]、PCJBF[1]、AR[3]和本文算法的输出结果分别与真实深度图像作差所得的结果。由图6可知,本文算法的误差线条相对于其他几种算法明显较少,可以证明本文算法对不连续的深度区域处理较好,能有效减小误差。

图6 算法实验误差图像Figure 6 Algorithm experiment error image
4 结论
针对目前的算法存在输出实验结果中边缘区域不清晰、平滑区域出现伪像以及处于不同区域像素点之间的影响较大导致输出错误的深度值等问题,本文基于HR深度伪矩阵提出自适应参数与边缘点引导的深度值重建的算法。首先利用Sobel算子对LR深度图进行修正;其次利用加入一系列自适应参数的自适应自回归模型完成深度不连续区域的深度重建。由实验结果可知,本文算法与其他算法相比,在采样因子为2、4、8时,Art、Books、Dolls等6幅图像上均取得了最低的BPR值,并且在主观视觉上取得了较好的结果。下一步将结合图像分割[9]的方法针对深度不连续区域完成深度图像超分辨的相关工作。
