柔性电涡流式触觉传感器性能仿真与分析

张 芮，朱姿娜

(上海工程技术大学机械与汽车工程学院，上海 201620)

0 引言

智能化是未来机器人发展的重要方向，而柔性触觉传感技术是智能化机器人的发展基础，它可以使生物感知外部的各种变化，采集来自外部的压力、振动、形状、纹理等相关信息，具有强敏感感知能力。目前，根据不同原理，柔性触觉传感器可分为：电容式、压电式、压阻式、电磁式和光学式等。其中电磁式触觉传感器因其输出功率高、动态响应范围大、灵敏度高等优点，成为国内外触觉传感器的重点研究方向之一。

常见的电磁式柔性触觉传感器主要包括电涡流式和电霍尔式。H.B.Wang[1]等用带有4个金属线圈的FPCB、柔性聚合体和铝箔制备了基于涡流原理的三维力传感器。T.Kawasetsu[2]等利用铁磁标记复合物代替铝箔制备了全柔性电涡流式三维力传感器。S.Youssefian[3]等采用硅橡胶制备了一种半球壳形状的电霍尔式柔性触觉传感器。现有研究中的传感器均在力学检测某些方面达到了一定要求，但是普遍仍无法实现综合检测要求，如尺寸太大，无法贴附在机器人手指处；高密度化阵列引起大量接线位置排布繁琐和信号干扰；难以兼顾力检测范围和分辨率等。针对以上问题，本文提出一种基于电涡流原理，由平面微线圈、弹性体和金属板组成的柔性触觉传感器，其优点如下：整体尺寸微小，可多个阵列附着在手指上，不会受到信号串扰影响；结构简单，施加接触力的表面没有任何电线连接，损坏的表面易于更换；线圈采用平面螺旋结构，可获得低电阻高电感，提高传感器的灵敏度。在仿生机器人手指上的应用如图1所示。采用有限元分析法对所设计的传感器进行模拟仿真，根据实际情况建立几何模型并赋予合适的材料属性，施加磁场和力场对模型设置边界条件，对影响其性能的结构参数和外部条件进行分析，为传感器的设计和制备提供借鉴。

图1 仿生机器人手指触觉传感器

1 电涡流触觉传感器的设计和工作原理

电涡流触觉传感器的设计原理如图2(a)所示，根据法拉第电磁感应定律[4]，当传感器中的激励线圈通入正弦交变电流I1时，线圈周围将会产生正弦交变磁场H1，使得位于该磁场的金属导体表面产生感应电流即涡流I2，该涡流I2又产生新的交变磁场H2，H2会阻碍原磁场H1的变化，使得传感器的等效阻抗Z改变，其变化程度主要取决于金属板的电导率σ、磁导率μ、尺寸因子τ、线圈与金属板间距d、电流i以及激励频率f等，即Z=F(σ,μ,τ，d,i,f)，当线圈和金属板的材料尺寸确定后，即除d外其他参数均不发生变化，则阻抗Z成为间距d的单值函数，这就是利用电涡流效应实现触觉感知测量的主要原理。

工作原理如图2(b)所示，当函数发生器向微线圈提供激励电流时，通过线圈的电流在其周围产生磁场，电磁场在金属板表面感应出电涡流，涡流将导致线圈的感应电压发生变化。当仿生柔性手指接触物体并存在力时，金属板与线圈之间的距离将会发生改变，其变化会影响涡流值得变化，基于对线圈感应电压和阻抗的测量，机器人可以准确地感知物体。

(a)电涡流触觉传感器设计原理

2 电涡流触觉传感器有限元模型

利用COMSOL Multiphysics有限元分析软件，建立参数化模型，模拟仿真触觉传感器在实际中的操作应用。

2.1 仿真模型的建立

因所设计的传感器各部分呈轴对称分布，空间电磁场和载荷分别以固定频率和力对称分布，可将空间涡流场和力场的三维几何模型简化成二维轴对称空间平面分析[7]，电涡流触觉传感器的二维等效模型如图3(a)所示，其中各部分的组成参数为：空气场是高度为1 100 μm、宽度为3 000 μm的矩形，金属板是高度为200 μm、宽度为2 200 μm的矩形，线圈半径为50 μm、螺距为185 μm，金属板与线圈的初始距离d=500 μm。考虑到高电感、低阻抗等特点，线圈匝数N=10，其二维模型及尺寸参数如图3(b)和表1所示。

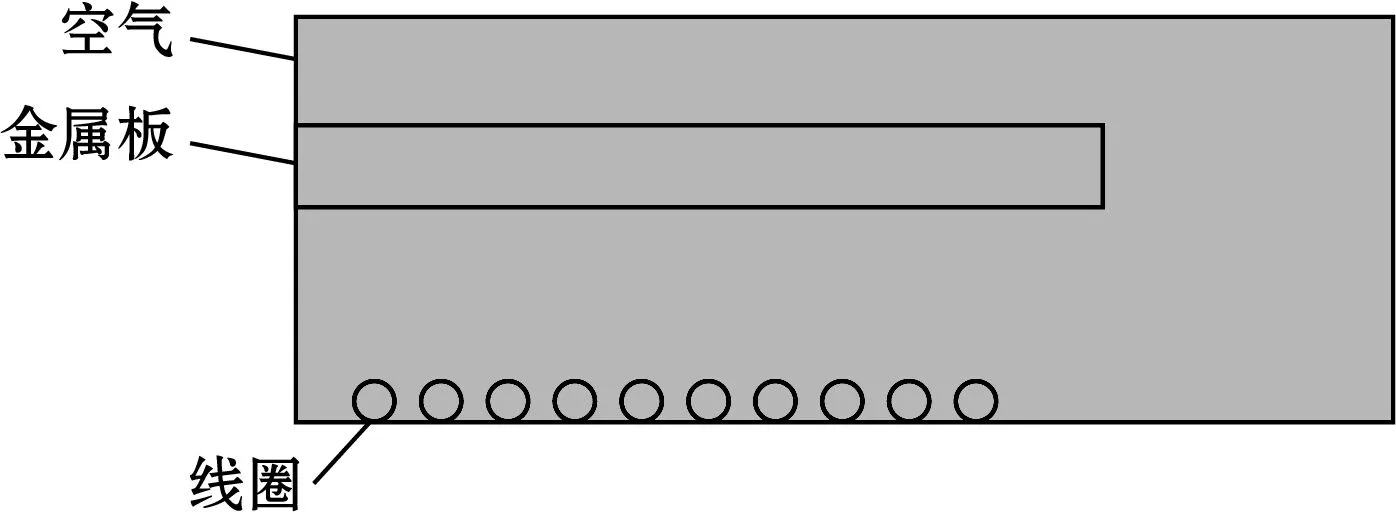
(a)电涡流触觉传感器的二维等效模型

表1 线圈几何尺寸参数

2.2 材料属性设置

空气区域的材料选择空气，金属板和线圈材料分别为铝和铜，各部分材料的电导率σ、相对磁导率μr和相对介电常数εr如表2所示。

表2 材料参数

2.3 求解域的设置及物理场的添加

2.3.1 设置求解域

由空气区域、金属板和线圈构成的求解区域[8]，其磁矢量势A由式(1)计算：

(1)

由电流密度产生的电流为：

(2)

式中s为电流穿过的曲面。

2.3.2 添加物理场

在磁场中设置线圈激励电流信号1 mA，传感器模型外部边界和对称轴选用狄利克边界条件，即磁矢势A=0，外部边界条件设置为磁绝缘。力学边界条件载荷施加在金属板表面，为方便计算，选择施加方式为压强，法向压强pZ和切向压强pX的变化范围均为0～1 000 kPa，以100 kPa为递增量连续加载。

2.4 网格划分

本文研究的内容主要是线圈与金属板，为了更好地贴近实际情况得出仿真结果，如图4所示，线圈和金属板处的网格划分很细密，其余部分的网格随着与线圈和金属板距离的增大而逐渐变大。

图4 二维模型的网格划分图

3 仿真结果与分析

3.1 激励频率对电涡流触觉传感器性能的影响

激励频率f=0时的初始状态下磁场分布情况如图5(a)所示，靠近线圈中心的磁感应强度B较大，最大值267.52×10-8T，最小值6.53×10-8T。图5(b)是线圈电流密度模S的分布情况，最大值为55 523.266A/m2，越靠近线圈中心S值就越大。

(a)初始状态磁感应强度分布

设置激励频率f范围1～15 MHz，以2 MHz递增，经过求解与后处理，在不同的激励频率下磁场与磁感应强度B、感应电压U、电阻R和电抗X以及电涡流S的变化情况如图6所示。根据图6(a)，B和U随着f的增大而逐渐增加。图6(b)为f与R和X的关系变化，二者均与f成正相关关系。由图6(c)可知，S随着f的增大而成几何倍数的增加，而电涡流集肤层深度δ逐渐减小。根据传感器的工作原理，S越大传感器的灵敏度越高。根据仿真结果，当f分别为1、3、5、7、9、11、13、15 MHz时，δ分别为230、133、103、87、77、70、64、60 μm，根据集肤层深度计算公式[9-10]：

(3)

可得出电涡流渗透深度为230.2、132.9、102.9、87、76.7、69.4、63.8、59.4 μm，仿真分析的结果与理论计算的数据相一致。为保证电涡流强度和集肤层深度，以及线圈的阻抗和电感电压，综合考虑选择激励频率f0=3 MHz。

3.2 线圈与金属板间距对传感器灵敏度的影响

传感器在实际应用中，当间距d发生变化时，磁感应强度B、阻抗Z和感应电压U等参数也会发生改变，通过检测电路可以获得触觉反馈信息。

设置激励频率f0=3 MHz，间距d分别为500、400、300、200、100、0 μm，B的变化情况如图7(a)所示，随着d减小，B呈下降趋势；在图7(b)中，当d=100～500 μm时，Z值随着d的减小而逐渐降低，而当d=60～100 μm时，Z随着d减小缓慢下降，当d=0～60 μm时，Z随着d减小而增大，并且增加的速率逐步上升；图7(c)则表示U与d之间的关系，其变化规律与Z相同。这是因为在d减小的同时，S逐渐降低，而当d=0～100 μm时，S先缓慢减小，随后增大，并且增大幅度逐步提升，这是影响阻抗和感应电压变化的重要因素，也是磁场强弱的另一种体现方式。

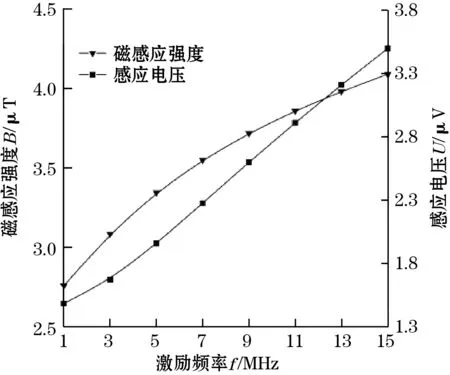
(a)磁感应强度和感应电压与激励频率f的关系

3.3 单维载荷对传感器性能的影响

当对金属板表面施加单维法向载荷和切向载荷时，间距发生改变，可以得到压强与金属板位移变形量和阻抗电压的数值变化关系。施加压强时金属板位移变化规律如图8所示，当单独施加法向压强或切向压强时，金属板位移与其压强均是正相关的一次函数关系，拟合后的函数表达式为：

0.041 1pZ+0.020 7=w1

(4)

0.084 2pX+0.018 7=w2

(5)

(a)d=0～500 μm时磁感应强度的变化

图8 压强与位移的变化关系

式中：pZ、pX为法向压强和切向压强；w1、w2为对应的位移变形量。

由函数表达式(4)、式(5)可以得知，法向压强引起的位移变形比切向压强要小。

(a)法向和切向压强与磁感应强度的变化关系

由图8可知，随着压强的增大，金属板与线圈间距逐渐减小。根据仿真结果绘出压强与磁感应强度B、电压U和阻抗Z的变化关系如图9所示。由图9(a)可知，当对金属板分别施加法向和切向压强时，B随着压强的增大而增大，显然切向压强磁感应强度的大小和变化率均比法向压强的大。由图9(b)可以得知，当金属板受到法向压强和切向压强时，U随压强增大而逐渐降低，可视作成负相关的一次函数关系，并且切向压强的U范围和变化率更大。通过图9(c)可以看出，对金属板分别施加法向和切向压强，Z与压强呈负相关的一次函数关系，施加切向压强时Z的变化率比法向压强的大。当金属板受到法向压强时，仅在法向产生位移变化，当受到切向压强时，金属板不仅在切向产生位移变化，同时在法向也产生位移变化。根据仿真结果，显然磁感应强度、电压和阻抗对切向载荷更加敏感，即相比于法向载荷，该传感器对切向载荷的灵敏度和分辨率更高，并且测量范围更广。

4 结论

本文所提出传感器最大的优点在于表面采用柔性可拉伸橡胶，与线圈和测量电路分离，并且只包含单个线圈，这种设计的传感器优点为：表面有良好的弹性，对施加的接触力具有耐久性；保护电路，易于更换，延长传感器的使用寿命；减小传感器的整体结构，可以多个附着于仿生手指上而不会产生信号干扰。采用有限元分析，研究激励频率对电涡流触觉传感器电磁特性的影响、金属板与线圈间距变化和金属板受到不同方向载荷时对传感器性能变化的影响，得出以下结论：

(1)激励频率对电涡流触觉传感器电磁特性的影响主要是电涡流强度和电涡流集肤层深度2个方面。随着激励频率的增大，电涡流集肤层深度逐渐降低，而电涡流强度却逐渐增强，磁感应强度和电阻电抗也随之增大，根据电涡流触觉传感器的工作原理和各参数值的变化情况，选择激励频率f0=3 MHz。

(2)线圈与金属板的间距对磁感应强度的变化影响不大，但是当间距逐渐减小时，金属板表面的磁场越来越强，电压、电阻和电抗则随之降低，由于电流密度模的影响，当间距d=0～100 μm时，电压和电阻随着间距减小先缓慢下降，然后逐渐提高，并且增长率逐步上升。为提高传感器的检测灵敏度，应尽量减小线圈与金属板的间距，使d保持在100～500 μm之间最为合适。

(3)对金属板施加同等量级的单维法向和切向载荷时，切向载荷加载时的位移形变、磁感应强度、电压和阻抗的变化率比法向载荷加载时变化率大，更为敏感，故单维切向载荷比法向载荷的灵敏度和分辨率高，测量范围更广，且均和金属板位移形变构成正相关的一次函数关系，这样可以方便得出单维载荷与金属板位移的变化关系。

通过以上仿真研究分析，可以为电涡流触觉传感器的设计和实验提供参考。