基于柔性铰链的增敏型FBG加速度传感器

洪 利，陈依柳，滕云田,2，张钰梓，邱忠超

(1.防灾科技学院电子科学与控制工程学院，河北廊坊 065201；2.中国地震局地球物理研究所，北京 100081)

0 引言

微地震监测在石油工程、核废料处理、大坝、危险性结构的预防和稳定性监测有广泛的应用[1],其信号与常规地震信号相比具有能量弱，频率高，容易被吸收等特点，这就对其信号的采集提出更高的要求[2-3]。与传统的电学加速度传感器相比，光纤布拉格光栅(FBG)加速度传感器以其体积小、质量轻、抗电磁干扰、耐腐蚀、易于实现分布式测量等优点越来越受到重视[4-5]。

近年来，国内学者根据FBG应变传感原理设计了多种形式的FBG传感器[6-7]，然而，适用于中高频领域的加速度传感器研究较低频领域仍有不足[8-10]。由于加速度传感器的固有频率和灵敏度相互掣肘，而中高频加速度传感器所需的高固有频率决定其灵敏度较低，所以研究提高中高频光纤光栅加速度传感器的灵敏度具有重要意义[11]。

针对中高频光纤光栅加速度传感器灵敏度低的问题，本文提出了一种带有2个惯性质量块的三铰链加速度传感器新型结构。从理论给出了传感器的灵敏度和谐振频率公式，并讨论了结构参数对传感器灵敏度和谐振频率的影响，利用有限元法分析了传感器的静态和动态特性，制作传感器实物并对其有效性进行验证。

1 传感器设计

1.1 传感器结构

传感器的结构如图1所示，该传感器是基于3个铰链的新型FBG加速度传感器，由底座、3个带有惯性质量块的椭圆柔性铰链以及光纤光栅组成。

图1 传感器结构示意图

该传感器可由一整块弹簧钢经过线切割和热处理一体化加工而成，形成一个不可分割的整体。将光纤光栅粘贴在2个惯性质量块中间，并使光纤光栅有一定的预拉量。

当产生振动,2个质量块会围绕各自的铰链微幅转动，质量块产生的惯性力会带动光纤光栅发生轴向的微小伸缩形变，从而导致FBG反射波长发生漂移。由于中间的铰链连接，2个质量块同时振动，上下光栅两端的形变方向相反，因而可达到灵敏度倍增的效果，并能消除温度变化带来的影响。

1.2 传感器灵敏度分析

传感器力学模型如图2所示，当振动激励信号加速度a作用在传感器敏感方向时，质量块因为惯性力产生振动。

图2 传感器力学模型

由于传感器完全对称，左右椭圆柔性铰链相对于中心铰链的位移的大小始终相同，可以提取结构的左半部分进行分析。整个系统在惯性力作用下达到转矩平衡，得到式(1)。

(1)

式中:m为质量块的总质量；d为质量块质心与铰链中心的距离；Δl为光纤的拉伸距离；2b为椭圆铰链长轴，2c为椭圆铰链短轴；e为惯性质量块宽度；h为惯性质量块高度；k为光纤的弹性系数；K为铰链转动刚度；θ1为两端铰链转动角度；θ2为中心铰链转动角度。

光纤弹性系数k为

(2)

式中:Af为光纤横截面积；Ef为光栅弹性模量。

质量块质心与铰链中心的距离d为

d=b+e/2

(3)

铰链转动刚度K为

(4)

式中：E为材料的弹性模量；w为铰链的厚度；t为铰链间最小厚度。

u表示为

(5)

式中s=c/t。

(6)

传感器灵敏度为光纤光栅的中心波长变化量和加速度a之比，S即FBG加速度传感器灵敏度，S为光栅的中心波长变化量和加速度a之比，即

(7)

式中：Pe为弹光系数；λB为光栅的中心波长；εf为光纤应变；在下文中的所指的灵敏度为峰-峰值灵敏度为2S。

1.3 传感器谐振频率分析

谐振频率f是加速度传感器的另一个重要参数，与传感器的可用带宽相关。为了求得传感器的谐振频率，设质量块绕铰链中心转动的转动惯量为J，动力学方程为

(8)

整个系统的谐振频率f为

(9)

其中转动惯量J为

(10)

2 结构参数影响及优化

2.1 结构参数对传感器的影响

传感器的灵敏度和谐振频率在一定条件下可以是负相关。例如，当提高质量块的质量m时，加速度传感器的灵敏度会上升，而其整体的谐振频率会下降。想要在所需的测量范围内获得更高的灵敏度，则需要对传感器的结构参数分析。利用matlab对传感器关键参数b、c、t、e、h分析。传感器材料为304不锈钢，其弹性模量为190 GPa，密度为7 850 kg/m3，传感器厚度为15 mm，光纤的横截面积为1.23×10-8m2，弹性模量为72 GPa，弹光系数为0.22，光栅的中心波长为1 550 nm，l为5 mm。

第1组分析b和c在t=0.5 mm、1 mm和2 mm时对传感器灵敏度和谐振频率的影响，令e=5 mm、h=30 mm、0 mm≤b≤8 mm、0 mm≤c≤8 mm，得到传感器灵敏度如图3(a)所示，谐振频率如图3(b)所示。

(a)不同t时灵敏度随b、c的变化

由图3可知，当b变化时，灵敏度变化较大，而谐振频率变化较小；当c变化时，灵敏度变化较小，而谐振频率变化较大；而t变化时对灵敏度和谐振频率的影响都很大。

第2组分析e和h在t=0.5 mm、1 mm和2 mm对传感器灵敏度和谐振频率的影响，令b=5 mm、c=3 mm，0 mm≤e≤10 mm，20 mm≤h≤35 mm，得到传感器灵敏度如图4(a)所示，谐振频率如图4(b)所示。

(a)不同t时灵敏度随e、h的变化

由图4(a)和图4(b)可知,当e变化时，灵敏度变化较大，而谐振频率变化较小；当h变化时，灵敏度变化较小，而谐振频率变化较大；而t变化时对灵敏度和谐振频率的影响都很大。

2.2 结构参数优化

由图3和图4可知，铰链的结构参数b、c和t发生微小变动时，会引起传感器性能的极大变动，而质量块尺寸e和h在一定范围的变动时，对传感器性能的影响较小。为了得到较理想的灵敏度和谐振频率，取c=5 mm,h=30 mm,采用Lingo优化软件对传感器的铰链参数b、e和t进行最优化设计。优化模型为：

MaxS

为了便于加工优化将结果取整数,模型参数如表1所示。

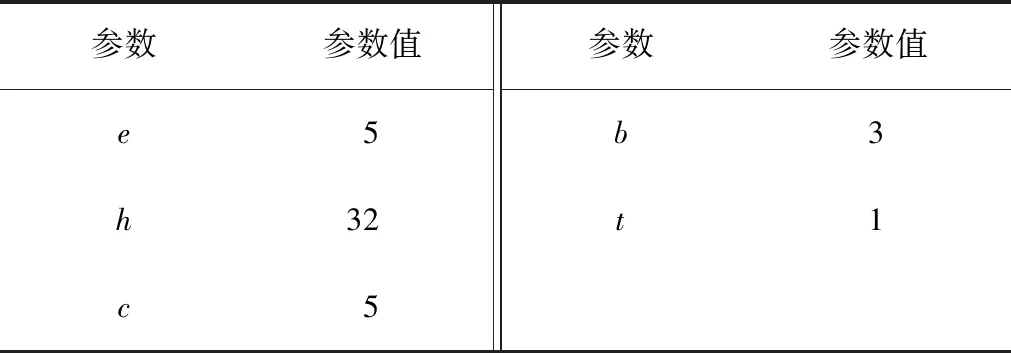
表1 模型优化参数 mm

3 有限元分析

为了分析传感器的振动传感特性，使用ANSYS对传感器进行分析。在SOLIDWORKS上建模，传感器中部件的材料性能参数见表2，将模型导入ANSYS使用WORKBENCH对传感器模型进行模态分析。将模型网格划分，在壳体下表面施加固定约束，运行后得到效果如图5所示。

表2 有限元模型结构材料参数

(a)一阶模态

由图5(a)可知，该结构一阶模态的固有频率1 449 Hz,且2个惯性质量块的运动方向相反。由图5(b)可知，该结构的二阶模态频率约为2 945 Hz,与一阶模态频率相差较大。而传感器的模态频率越大，其结构刚度越大，因此，一阶模态刚度与二阶模态刚度之间的差异也很大。结果表明，该结构的交叉耦合很小，能够满足传感器测量精度的实际要求。

4 实验与分析

传感器标定实验如图6所示，函数发生器发出信号经过功率放大器后驱动激振台输出相应的振动信号，加速度传感器接受到振动信号使反射光谱产生变化；解调仪把光信号转换成电信号，通过计算机进行实时显示并记录数据。

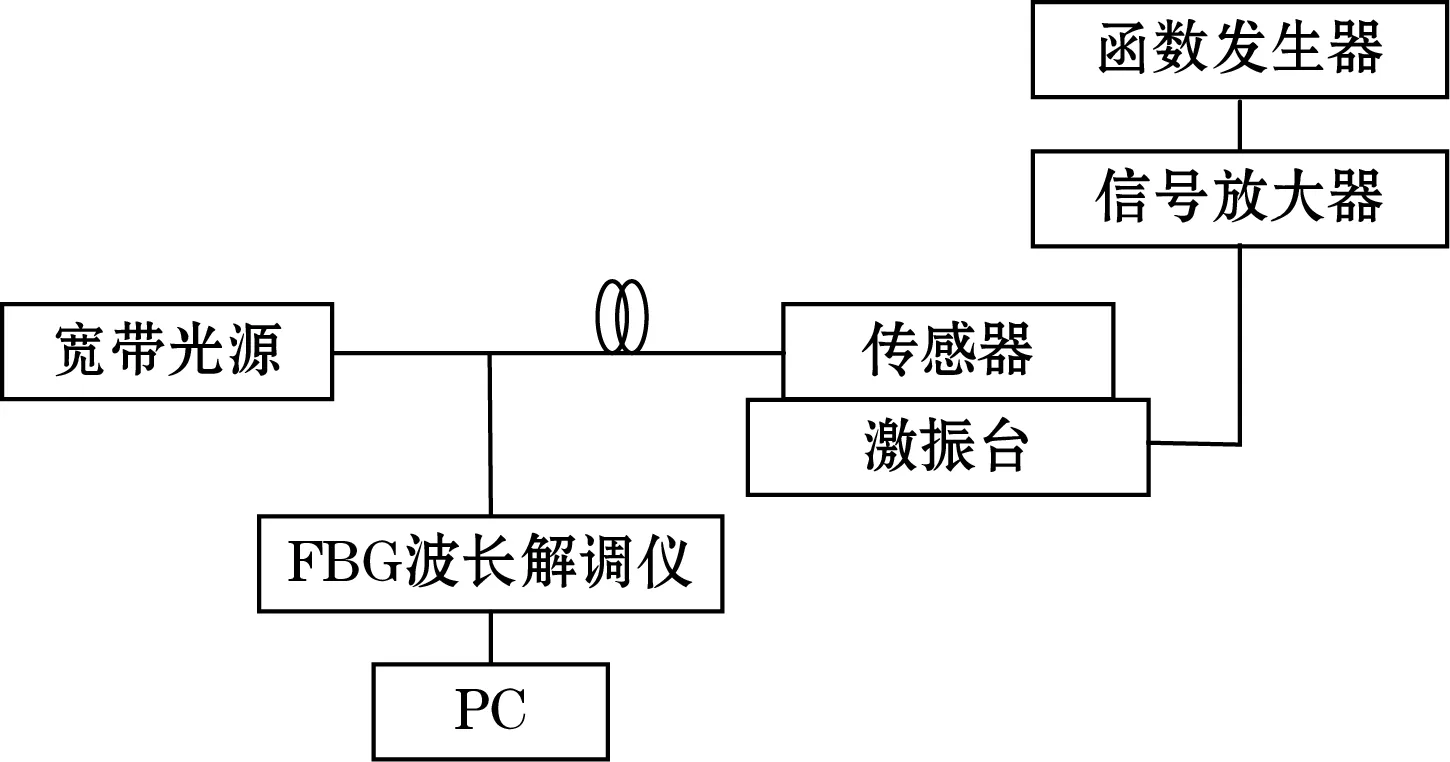
(a)系统流程图

4.1 频率响应实验

频率响应曲线决定传感器的频带范围，因此必须对所研制的传感器进行动态标定。在传感器幅频测试中输入10 m/s2的加速度作为恒定加速度值，首先测量在15 Hz时传感器的波长变化量，然后频率从100 Hz开始,每次递增100 Hz作为1个步长分别记录波长变化量，结果如图7所示。

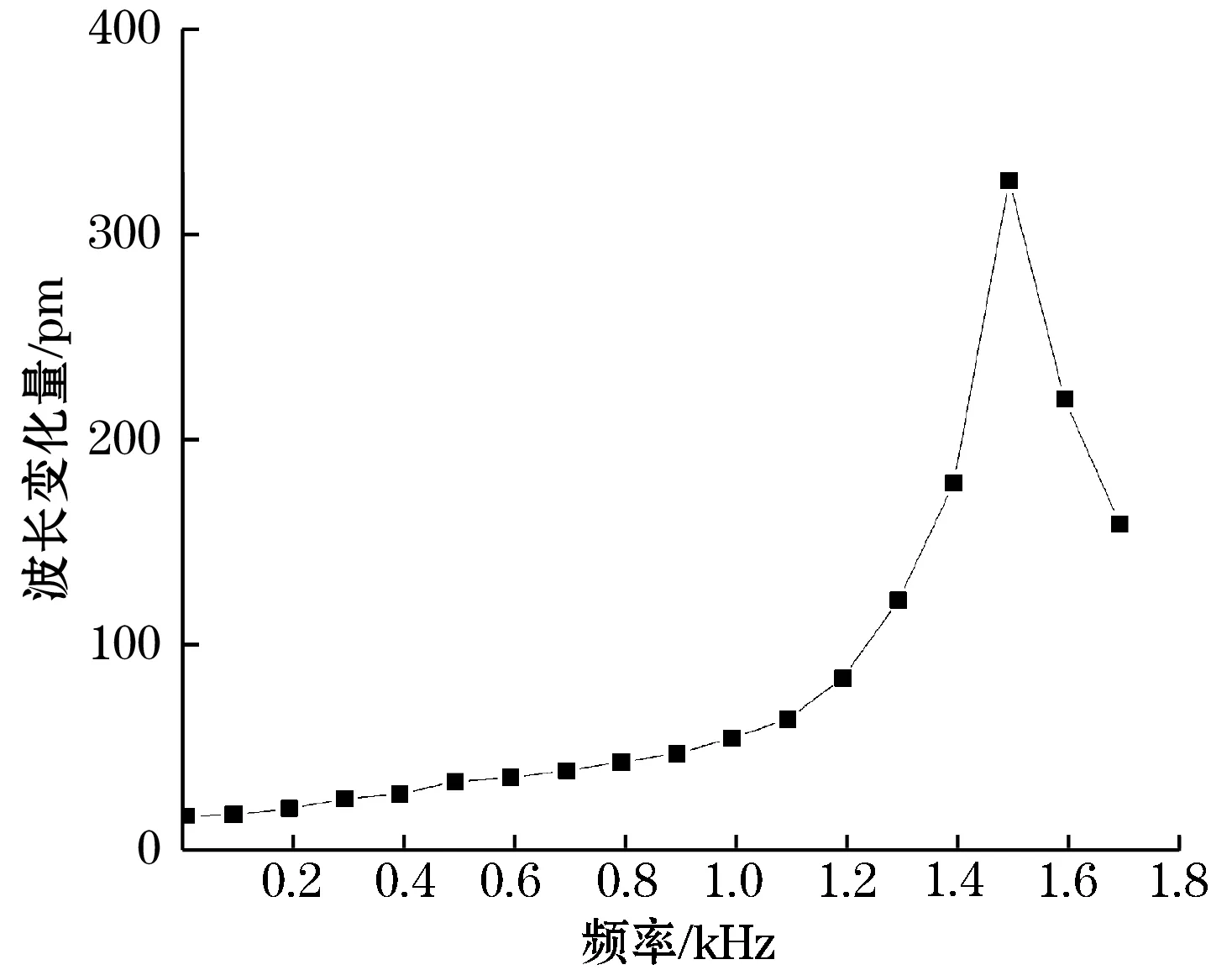
图7 传感器幅频响应特性

结果表明,该传感器在15～1 000 Hz具有较好的平坦度，在约为1 500 Hz达到波长变化的最大值。因有限元法中均没有考虑到光纤的预应力，且实际装配传感器材料属性与有限元仿真中材料属性不同，从而导致传感器的一阶频率实验值与理论值不同。

4.2 灵敏度系数测试

传感器灵敏度标定选择使用160、325、495 Hz作为测试频率，加速度值从1 m/s2变化到16 m/s2，改变激振台的加速度大小，使光纤加速度传感器在不同加速度下运行，绘制波长漂移值随加速度变化曲线，结果如图8所示。

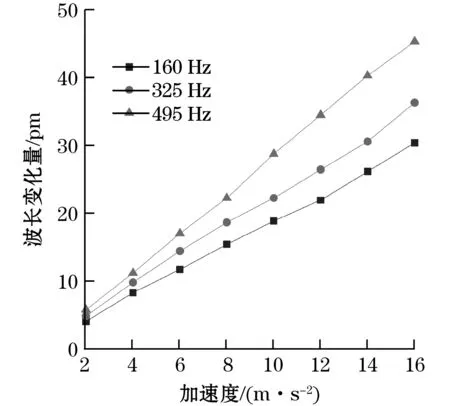
图8 传感器灵敏度标定曲线

结果表明该传感器在频率为160 Hz、325 Hz、495 Hz时波长变化量随加速度的提高具有良好的线性度，灵敏度约为18 pm/g。

4.3 横向抗干扰能力

由于FBG加速度传感器是单自由度的，其横向抗干扰能力也是不可忽视。在实验过程中，调整FBG振动传感器，使其测量方向垂直于激振器的振动方向。振动信号的振幅保持在10 m/s2，频率为325 Hz，结果如图9所示。

图9 传感器横向特性

结果表明，该传感器敏感方向的漂移量约20 pm,非敏感方向的波长变化量不超过1.8 pm，由此得出该传感器的横向抗干扰度小于10%。

5 结束语

考虑到FBG在震动监测中的优势，根据微地震中的加速度信号具有的中高频特性设计了一种新型结构的FBG加速度传感器。通过数值分析方法讨论了结构参数对传感器固有频率和灵敏度的影响，采用有限元仿真分析传感器结构特性，制作传感器实物并对其有效性进行验证。结果表明，该光纤光栅加速度传感器固有频率为1 500 Hz，传感器灵敏度可达18 pm/g，并具有较好的横向抗干扰能力，为光纤光栅加速度传感器在微地震监测的工程应用提供了一种新的方法。