基于动静态安全场的机器人避障路径控制仿真研究
2021-07-08许艳英
张 郭,许艳英,张 亮
(1.重庆科创职业学院人工智能学院,重庆402160;2.西南交通大学机械工程学院,四川成都610031)
随着自动化程度地提高,机器人在社会发展中迅速占领了市场,主要应用于汽车、电子、医疗、航空及矿产开发等领域[1-2]。当前,单臂机器人经过多年的改进日趋成熟,在生产流水线上应用较多,但是面对复杂任务或者多重任务时,不能进行协调和配合,受到了一定的局限性。双臂机器人的诞生,不仅能够完成复杂任务,而且还提高了工作效率,但是其控制难度也在上升。国内双臂机器人研究起步相对较晚,与国外相比,机器人运动路径规划和协调控制方面还存在很大差距。因此,研究双臂机器人控制系统,对于打破国外机器人核心技术的封锁具有重要意义。
为了提高机器人避障反应速度,缩短机器人运动路径,提高机器人运动轨迹跟踪精度,国内外学者对机器人避障展开研究。例如:文献[3-4]研究了机械臂避障神经网络控制方法,创建了机械臂动力学模型,采用多层感知神经网络逼近原理,通过仿真验证避障效果,从而提高了机械臂轨迹追踪精度。文献[5-6]研究移动机器人避障的模糊神经网络控制方法,设计了移动机器人的总体构架,采用神经网络模糊控制规则,通过模糊推理提高控制系统的稳定性,具有较高的适应性和通用性。文献[7-8]研究了移动机器人模糊PID控制方法,推导出机器人运动方程式,设计了模糊PID控制流程,通过仿真验证机器人避障过程中产生的误差,提高控制系统的响应速度。但是,以前研究的机器人在动静态安全场环境中移动时,其运动路径就会变长,跟踪误差也随之增大。对此,本文定义了机器人运动的动态安全场,给出了安全场二维等值面简图。引用滑模控制器,采用卡尔曼滤波器对离散滑模控制器进行改进,通过Matlab软件对改进后的机器人避障效果进行仿真验证,为更好发挥机器人避障能力提供参考数据。
1 动静态安全场
1.1 基本定义
将在R3和局部参考系l中运动的一般刚体视为“危险源”,使得其一个点T的位置由r(tx t y t zt)T给出,而其速度在引入的坐标系中为零。用局部坐标系中r=[x y z]T和v=[v x v y v z]T分别表示P空间中一般运动点的位置、速度,如图1所示。
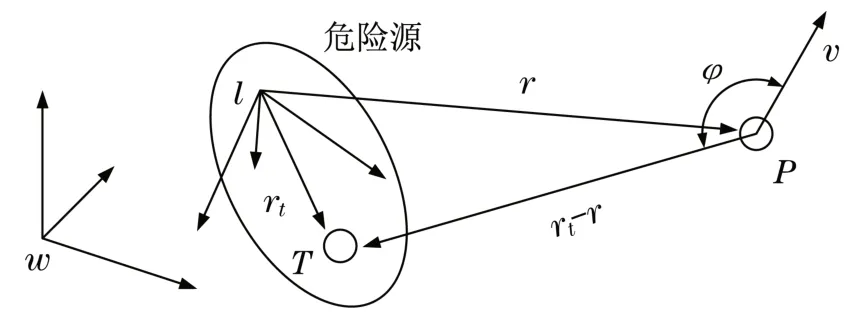
图1 危险源坐标位置Fig.1 Coordinate position of hazard source
运动的旋转角度[9]定义为

为了能够确定角度φ,其计算方程式为

采用下列函数表示由运动点质量在空间运动点上运动所引起基本运动静态安全场为
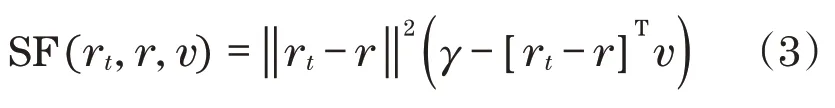
式中:γ为正常数。
γ需要满足下列关系式:
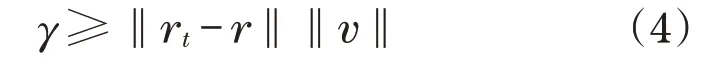
定义ρt=‖r t-r‖,v=‖v‖,则动静态安全场需要满足下列条件:

安全场明显受到距离的影响,如式(5)中所强调的,但它也捕捉到速度向量v的模块,表示危险源和计算场的点之间的相对速度以及偏角φ。根据式(6)可知,如果r点的运动指向r t点,则安全场随着速度的增大而减小。最后,式(7)意味着对于固定速度量级,安全场随着偏角φ的减小而减小。
1.2 动静态安全场
二维空间中运动质量T引起的安全场等值面如图2所示。安全场随着点质量和评估该场的一般点之间距离增加而增大,并且沿T的移动方向取较低的值。
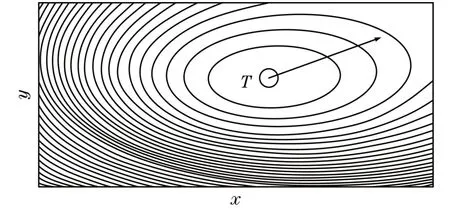
图2 安全场二维等值面Fig.2 Two-dimensional iso-surface of safety field
计算三角形网格离散的刚体安全场的第一步是将动态安全场的定义推广到R3内的三角形内。在局部固定的参考坐标系中,一旦用局部坐标表示,危险源的线速度和角速度均为零,用r S表示属于三角曲面S点的位置,其中r=(x y z)T和v=(vx vy vz)T分别为空间P中一般运动点的位置、速度。分别用r w、vw表示一般空间运动点的绝对位置和速度,如图3所示。知道局部坐标系的位置、线速度和角速度,在全局坐标系中分别用r O′、vO′和ω表示,在局部坐标系中就可以通过以下变换计算r和v:
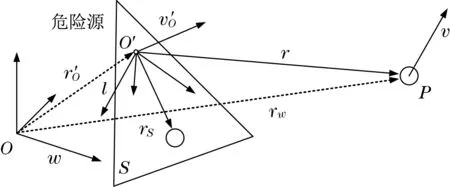
图3 动静态安全场运动简图Fig.3 Motion diagram of dynamic and static safety field

式中:Awl、Rwl分别为齐次变换矩阵和旋转矩阵;S(ω)为角速度张量的斜对称矩阵。
根据式(1),累积运动安全场定义为以下表面积分:
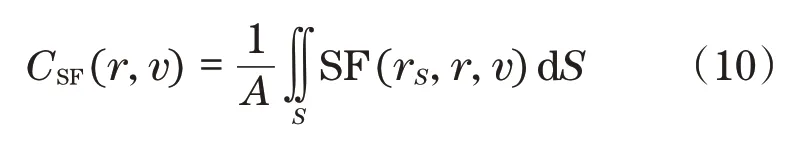
式中:A为三角形表面的面积。
曲面积分是可解的,从而可以推导出

安全区域为
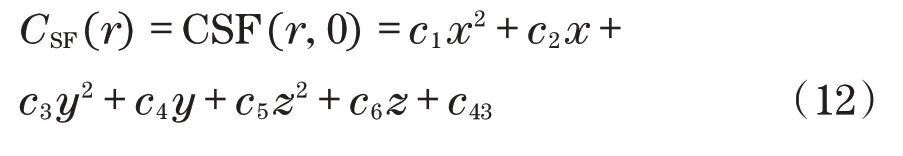
2 机器人运动控制
2.1 机器人设计规则
除了简单和灵活的危险评估之外,累积安全域可以用于多自由度冗余度机器人的控制,以确保机器人在执行规定的任务同时提高安全等级。设计原则是在机器人手臂的几个感兴趣点上,评估由刚体危险源产生的安全场。利用这一信息确定所考虑点的位移。基于安全域的位移应确保机器人手臂避开危险源,以防止机器人与危险源本身可能发生碰撞。
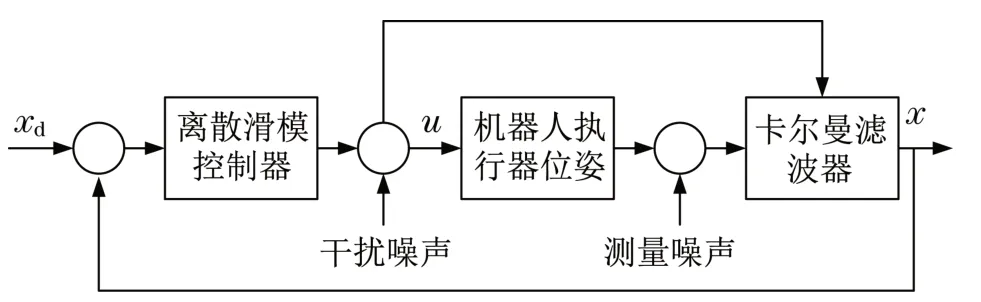
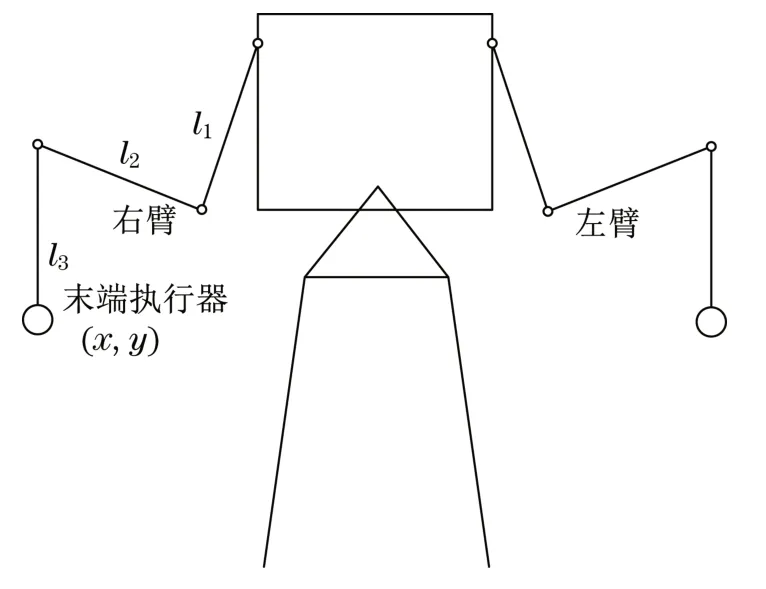
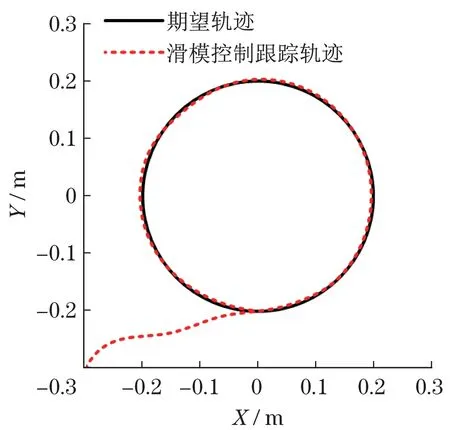
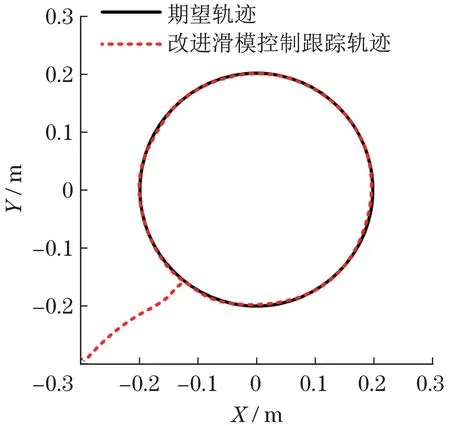
假设研究一个具有n个关节和广义坐标q∈Rn的机器人手臂。用m表示任务空间的维数,我们假设机器人在运动上相对于任务m 由于CSF(r,v)是在局部坐标系中定义的,为了在全局坐标系w中表示Δp0,利用从局部坐标系l到全局坐标系w的旋转矩阵Rlw。在多个危险源的情况下,捕捉到所有危险源影响的总位移由以下矢量给出: 一旦计算出回避位移,就可以通过将雅可比变换为相应的关节角增量Δq0,类似于闭环逆运动学算法。对于位于机械臂上点S的单个期望位移Δp0,通过以下方法获得相应的Δq0: 式中:kp为正实数;JS,v(q)为点S相关联的雅克比矩阵JS(q)的前三行。 假设采样时间为Δt,根据式(15)可以推导出机器人关节产生的角速度为 将信号q′0输入到位置、速度命令的闭环逆运动学算法中,其单臂控制角速度的解析表达式为 式中:q′T为任务相关的角速度;Ke为正定对称矩阵;xd、x分别为期望和实际位移;J(q)为相应的雅可比矩阵;J†(q)为雅可比矩阵右伪逆。 将机器人末端执行器运动传递函数进行离散化,得到机器人末端执行器位姿运动状态方程[11]为 式中:A为状态矩阵;B为输入矩阵;u(k)为系统的控制律;x(k+1)和x(k)为系统不同时刻的状态。 定义切换函数为 式中:Ce为控制参数。 定义指数趋近律函数为 式中:T为采样时间;q、ε为正实数;Δ为函数切换带宽度。 根据式(21)~式(23)可以推导出系统的控制律为 为了提高控制系统的稳定性,采样卡尔曼滤波器对控制系统噪声进行过滤,假设控制系统离散状态方程式[12-13]为 式中:X为状态矩阵;Φ为离散系统矩阵;H为测量矩阵;Y控制系统输出;W(k)为干扰噪声;Z(k)为测量噪声;Γ为噪声过滤矩阵。 卡尔曼滤波增益的计算过程如下: (1)系统状态预测过程,其方程式为 式中:X0为系统状态估计。 (2)系统状态更新过程,其方程式为 式中:Ka为卡尔曼滤波增益系数。 (3)协方差预测和更新过程,其方程式为 式中:P为协方差矩阵;R为方差;In为单位对角矩阵。 机器人采用卡尔曼滤波器的离散滑模控制流程如图4所示。 图4 机器人末端执行器位姿控制流程Fig.4 Pose control flow of robot end effector 为了验证机器人末端执行器避障效果,以机器人右臂为研究对象,如图5所示。采用Matlab软件对机器人右臂执行器跟踪进行仿真。假设机器人右臂期望运动位姿方程式为x2+y2=0.04。仿真参数为:右臂关节长度l1=l2=l3=0.6 m,末端执行器初始位置(x,y)=(-0.3,0.3),关节质量为m1=m2=m3=0.2 kg,障碍物半径为Rp=0.025 m,控制参数Ce=5,q=10。在静态安全场(无障碍物干扰)环境中,机器人采用滑模控制、改进滑模控制的轨迹跟踪效果分别如图6和图7所示。在动静态安全场(有障碍物干扰)环境中,机器人采用滑模控制、改进滑模控制的轨迹跟踪效果分别如图8和图9所示。 图5 双臂机器人Fig.5 Two-armed robot 对比图6和图7可知:机器人在静态安全场环境中,采用滑模控制方法,机器人在轨迹追踪过程中,搜索路径较长;采用改进滑模控制方法,机器人在轨迹追踪过程中,搜索路径较短。对比图8和图9可知:机器人在动静态安全场环境中,采用滑模控制方法,机器人在轨迹追踪过程中,遇到移动障碍物时,反应迟钝,在避开障碍物过程中,运动路径较长;采用改进滑模控制方法,机器人在轨迹追踪过程中,遇到移动障碍物时,能够提前做出反应,在避开障碍物过程中,运动路径较短。 图6 滑模控制跟踪(静态安全场)Fig.6 Sliding mode control tracking(static safety field) 图7 改进滑模控制跟踪(静态安全场)Fig.7 Improved sliding mode control tracking(static safety field) 图8 滑模控制跟踪(动静态安全场)Fig.8 Sliding mode control tracking(dynamic and static safety field) 图9 改进滑模控制跟踪(动静态安全场)Fig.9 Improved sliding mode control tracking(dynamic and static safety field) 因此,双臂机器人在动静态环境中跟踪轨迹时,传统滑模控制系统很难快速地做出反应,导致机器人在避障过程中,运动路径较长,跟踪误差较大。但是,采用卡尔曼滤波器对滑模控制器进行改进后,能够较好地抑制外界噪声的干扰,双臂机器人在避障过程中,缩短了运动路径,提高了轨迹跟踪精度。 本文研究双臂机器人避障路径和轨迹跟踪问题,设计了机器人的改进滑模控制器,在不同环境中对机器人运动路径跟踪误差进行仿真,主要结论如下:①机器人在静态安全场环境中运动时,采用滑模控制器,其运动路径较长,搜索能力较弱,而采用改进滑模控制器,其运动路径较短,搜索能力较强。②机器人在动静态安全场环境中运动时,采用滑模控制器,能够避开障碍物,但是反应速度较慢,导致运动路径较长,跟踪误差较大,而采用改进滑模控制器,反应速度较快,其运动路径较短,跟踪误差较小。③本文研究的双臂机器人避障运动路径和跟踪误差,在未来市场中具有重要的应用价值,但是机器人末端执行器运动速度和加速度变化情况,并没有展开研究,未来科研人员可以作为进一步研究课题。
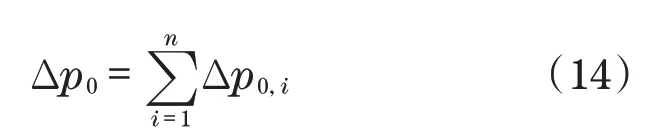


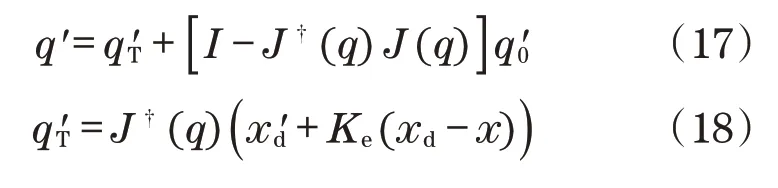

2.2 离散滑模控制器设计


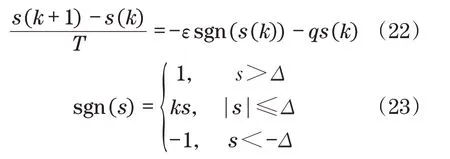


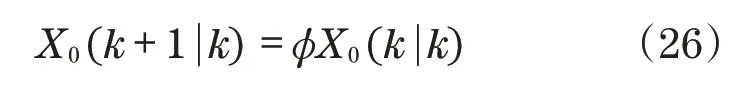


3 避障仿真及分析


4 结论
