基于非线性控制的直齿圆柱齿轮箱主动振动仿真研究

张建华，许衍彬

（1.保定理工学院工程技术学院，河北保定071000；2.河北科技学院智能制造工程学院，河北保定071000）

齿轮是很多机器传递扭矩的重要组成部分，无论是在企业生产加工中，还是在平时生活中，都能见到其身影。齿轮传动系统具有体积小、传动效率高及承载力大等许多优点，在社会发展中有着广泛的应用，主要用于采矿机械、汽车、海底探测和航空航天等许多领域［1-2］。随着科技的进步，生产设备也在不断升级，逐步向自动化和智能化方向发展。齿轮传动系统不可避免地要在复杂多变环境进行中进行传递扭矩。因此，对齿轮传动的误差、振动幅度的要求也越来高。若齿轮传统系统动态误差过大，不仅导致振动幅度增大，还会影响其使用寿命，造成重大经济损失。据不完全统计，在工业生产中，齿轮在传动系统中所占的比例已经达到了80%。因此，必须尽快研究齿轮传动振动控制方法，提高我国齿轮传动技术在市场中的竞争力。

为了降低齿轮传动系统输出误差，科研人员从多种角度对其展开研究。例如：文献［3-4］研究了电磁齿轮神经网络PID控制方法，创建了电磁齿轮动力学数学模型，引用PID控制器并进行改进，设计了神经网络PID控制器，采用Matlab软件对电磁齿轮控制器进行动态仿真，从而降低了齿轮传动系统的抖动幅度。文献［5-6］研究了直齿圆柱齿轮主共振控制方法，创建了直齿圆柱齿轮传动系统动力学模型，采用多尺度法对系统的振动特性进行分析，通过仿真验证啮合刚度对齿轮主共振的影响，从而得到最佳的匹配控制参数。文献［7-8］研究了齿轮箱振动主动控制的Fx RLS算法，介绍了Fx RLS算法的结构框图，建立齿轮箱振动主动控制结构，构建联合仿真系统，结果显示Fx RLS控制系统收敛速度快，从而有效地控制中低频振动。但是，以前研究的齿轮传动系统在受到不同频率和转速影响时，其输出动态误差就会增大，从而造成齿轮箱振动幅度上升。对此，本文建立了直齿圆柱齿轮的动力学模型，推导出齿轮刚度随位置变化方程式。设计了非线性控制方法，采用模型反演与前馈控制对非线性控制进行补偿，消除控制系统不稳定现象，并对齿轮输出动态误差进行仿真验证，为进一步研究齿轮主动振动控制方法提供参考价值。

1 齿轮动力学模型

过去提出了许多齿轮机构模型，这些模型包括不同的影响，并作出了不同的假设：齿隙、制造误差、渐开线齿廓误差和支承件弹性。本文研究了的齿轮机构忽略了轴承和轴的弹性。在该模型中，将齿轮机构建模为2自由度弹簧-质量系统，研究了动态载荷作用下的时变响应。

在准静态加载条件下，计算了齿轮在某些连续角位置的刚度。齿轮刚度计算公式为

式中：T为输入载荷；TE为传动误差。

最初的6自由度模型是一个多功能的模型，包含许多影响因素，由于间隙引起的非线性，在该模型中，轮廓误差和制造误差以及许多支承机械元件的影响可以作为离散单元，如轴、轴承的弹性和阻尼特性。然而，在首次尝试解决非线性控制问题时，发现简化为2自由度模型是很方便的。

本文考虑的动态模型，其CAD模型如图1所示。在这个模型中，齿轮由刚性轮表示，这些刚性轮通过多个元件连接在一起，代表齿轮齿廓中的柔度、齿隙和几何偏差。第1个单元是周期时变齿轮啮合刚度km（t）。第2个元件是黏滞阻尼器cm，用于表示齿轮啮合处的能量损失。位移函数e（t）也可沿作用线应用于模型制造误差、齿廓磨损或有意齿廓修改。最后将啮合刚度引入间隙单元，使齿隙引起的齿面分离能够精确建模。

图1 直齿圆柱齿轮的动力学模型Fig.1 Dynamic model of spur gear

为了简化6自由度动力学模型，建立2自由度半定扭转模型，提出了若干假设：轴、轴承的弹性和阻尼特性可以忽略。代表外形和制造误差的e（t）从方程中去掉。齿隙是每个齿轮总成的固有特性被忽略。未考虑装配误差，如中心距误差偏心和轴的几何约束，即假定轴处于完全平行状态。

这是一个具有非线性刚度项的直齿圆柱齿轮副的2自由度半定动力学模型，其刚度项随齿轮副的角位置周期性变化，其动力学模型［9-10］如下：

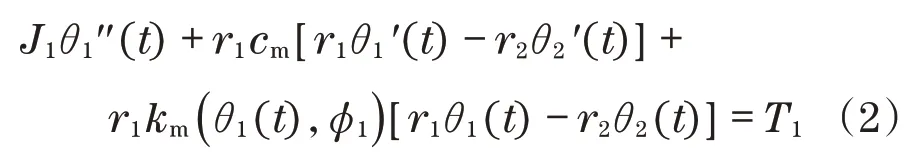
式中：T1、T2分别为控制扭矩和负载扭矩；θ1、θ2分别为小齿轮和齿轮的角位移；r1、r2分别为小齿轮和大齿轮的半径；km（t）、cm分别为齿轮系统的啮合刚度和阻尼系数；J1、J2分别为小齿轮和大齿轮的转动惯量。

刚度可以写成平均刚度项加上随时间变化的不确定部分的总和：

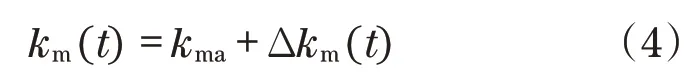
式中：kma为平均刚度；Δkm（t）为变化刚度。

啮合刚度是时间的函数，实际上是小齿轮和齿轮绝对角位置的函数。在第2种方法中，可变啮合刚度km（t）可以写成具有相位角的小齿轮角位置的非线性函数，相位角与小齿轮和大齿轮在模拟起始位置的绝对角位置有关。它可以写为

式中：θ1（t）为小齿轮的角位置；ϕ1为小齿轮相对角位置。

因此，这是刚度项和角度位置之间的非线性关系。任何具有可变啮合刚度的齿轮副绝对是非线性微分方程。

2 齿轮非线性控制

2.1 齿轮振动控制

直齿圆柱齿轮副系统的运动方程［11-12］可以用简洁的形式写成

式（6）可以分成如下两个部分：

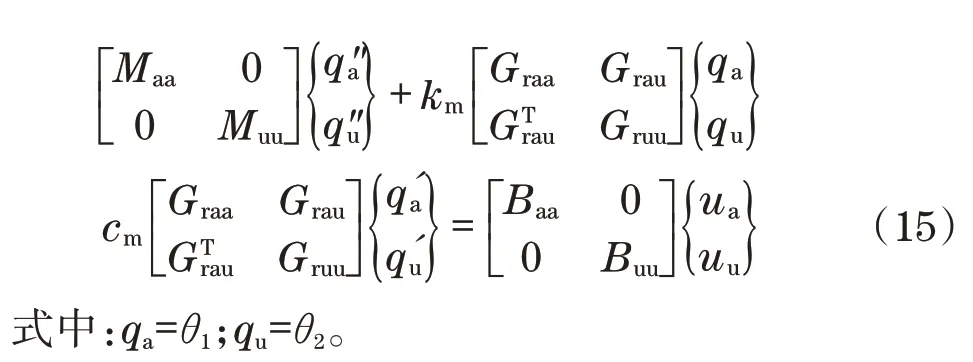
2.2 输入输出线性化

对于运动方程式（15），输入-输出法向形式和相关状态向量为

齿轮传动系统的线性化反馈律为

式中：v为新的输入。

当这个反馈定律应用于式（22）时，式（22）、式（24）可以变换为

为了使用反馈线性化技术，式（31）给出的内部动力学必须有界。为了确保内部动力学是有界的，必须研究零动力学，即ζ=0和v=0，并由下列式子给出：

对于有界内部动力学，线性化反馈律（29）可与PI控制器一起用于渐近输出跟踪。在这种情况下，跟踪控制由以下给出：

引入输出轨迹误差e=yd-y，并将控制律式（35）应用于线性化子系统，得到线性误差动力学为

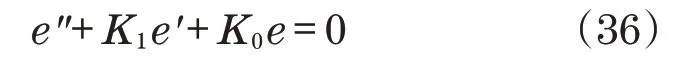
式中：K0、K1为误差控制常数。

期望的输出轨迹用ζd=［ζ1d…ζ2d］T表示，需要精确的得到所需输出y=ζ1d，则输入可从输入-输出公式，式（22）计算得到

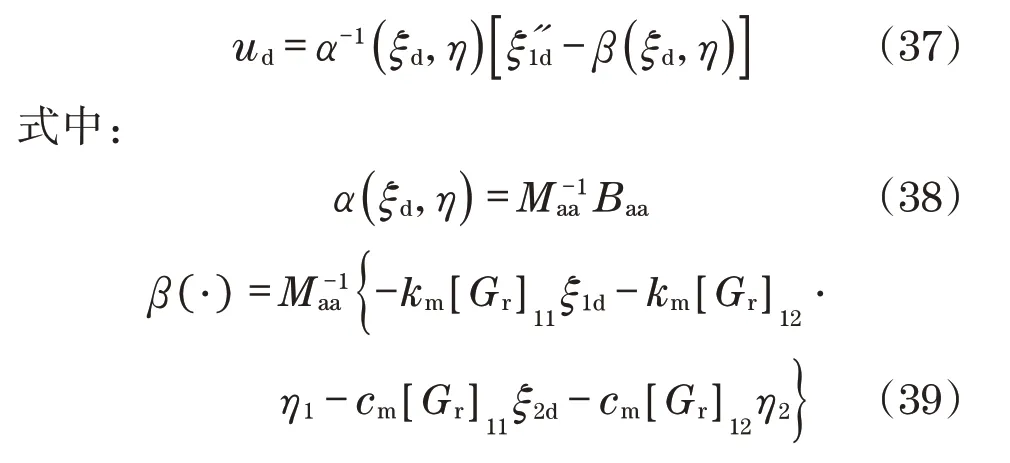
然而，状态η1、η2必须根据内部动力学的微分方程（23）和（24）计算，这表示驱动的内部动力学和非驱动坐标η必须始终满足下列条件：

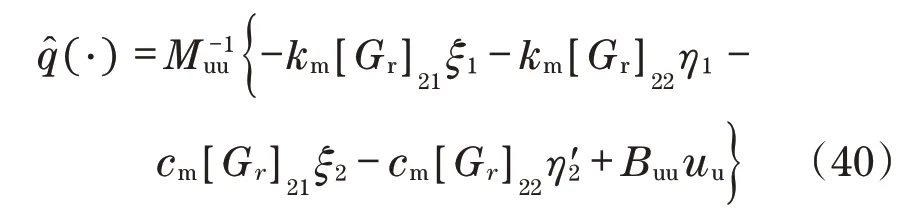
2.3 齿轮系统非线性控制

非线性控制器控制的齿轮系统的流程图如图2所示。小齿轮参考信号和测量的齿轮状态被发送到逆模型。逆模型块使用式（37）计算以所需驱动小齿轮速度的扭矩。在此方程中，ζd为参考输入，测量齿轮状态η并将其输入控制器。现在，作用在小齿轮上以使系统遵循所需输入的必要扭矩可以计算出来。此扭矩驱动系统，可以准确跟踪小齿轮所需的位移、速度和加速度。因此，为了使系统中不确定性具有鲁棒性，采用第2反馈PI系统监控小齿轮的误差状态，并将小齿轮状态下的误差趋近为零。根据式（36）可以得到PI控制器误差状态，需要小齿轮状态向量ζ。总的来说，系统有两个级联反馈回路，在这些反馈回路中使用全状态测量，即测量大齿轮和小齿轮的状态。逆模型的职责是消除非线性，PI控制器的职责是保证小齿轮的误差动态稳定。

图2 直齿轮非线性控制Fig.2 Nonlinear control of spur gear

3 仿真及分析

为了更好地检验直齿轮非线性控制系统输出动态误差，在不同状态下，采用Matlab软件对齿轮传动输出动态误差进行仿真验证。仿真参数设置如下：模数m=1 mm，小齿轮齿数Np=20，大齿轮齿数Ng=40，压力角Φ=20°，中心距d=30 mm，小齿轮内孔半径rpi=8 mm，大齿轮内孔半径rgi=8 mm，重合度cr=1.635，杨氏模量Ep=Eg=2×1011Pa。在不同振动频率下，采用线性控制、非线性控制的齿轮传动输出的动态误差分别如图3和图4所示。在不同转速条件下，采用线性控制、非线性控制的齿轮传动输出的动态误差分别如图5和图6所示。

图3 线性控制动态误差（不同频率）Fig.3 Linear control dynamic err or（different frequencies）

根据图3可知：在不同频率干扰下，采用线性控制方法，齿轮输出的动态误差较大，在1 500~2 000 Hz范围内，动态误差达到最大值为4.6×10-5m。根据图4可知：在不同频率干扰下，采用非线性控制方法，齿轮输出的动态误差较小，在2 000~2 500 Hz范围内，动态误差达到最大值为1.2×10-5m。根据图5可知：在不同转速状态下，采用线性控制方法，齿轮输出的动态误差较大，小齿轮在1 500~2 000 r/min范围内，动态误差达到最大值为4.8×10-5m。根据图6可知：在不同转速状态下，采用非线性控制方法，齿轮输出的动态误差较小，小齿轮在2 000~2 500 r/min范围内，动态误差达到最大值为1.0×10-5m。

图4 非线性控制动态误差（不同频率）Fig.4 Linear control dynamic error（different frequencies）

图5 线性控制动态误差（不同转速）Fig.5 Linear contr ol dynamic err or（differ ent speed）

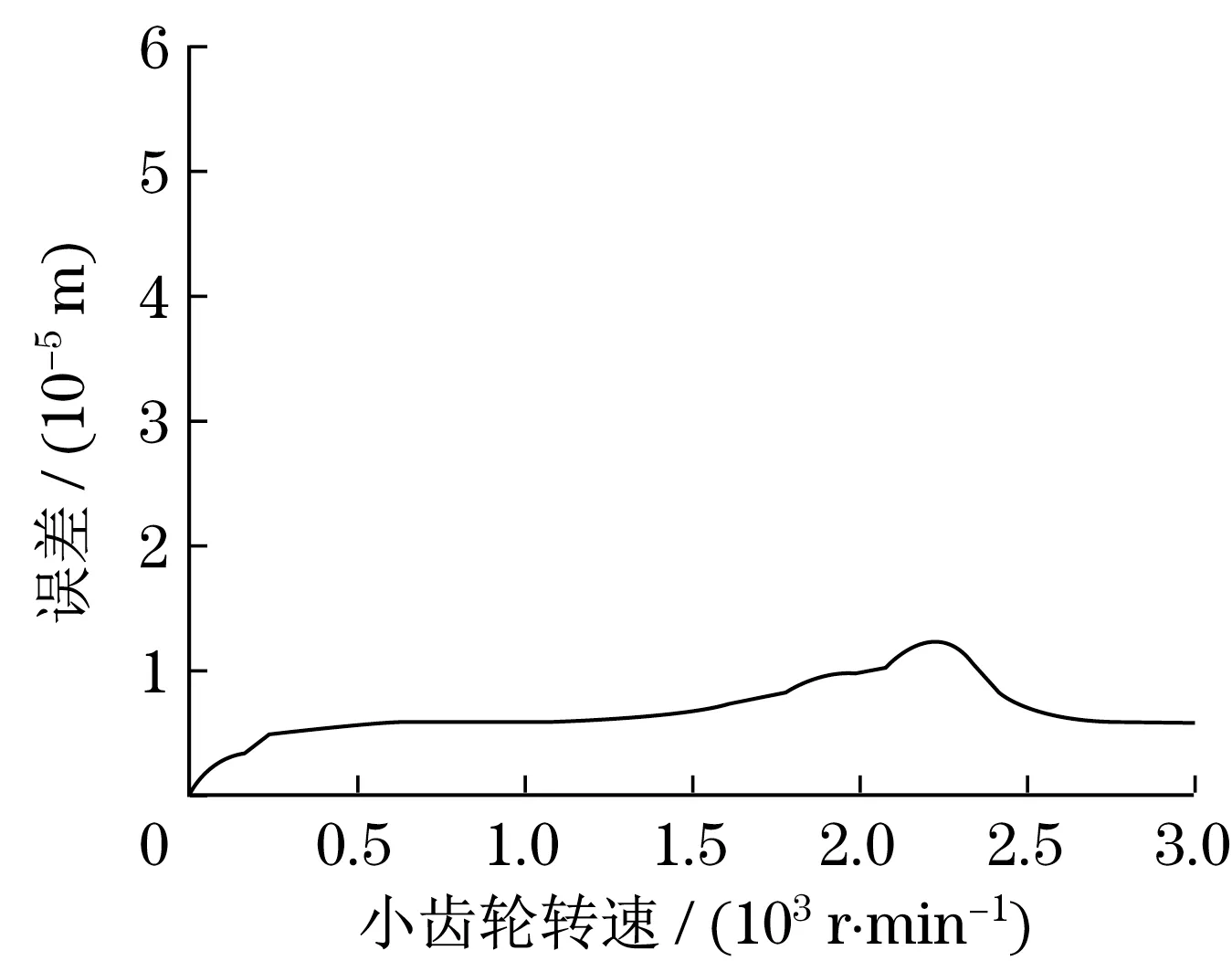
图6 非线性控制动态误差（不同转速）Fig.6 Nonlinear control dynamic error（different speed）

因此，本文设计的直齿圆柱齿轮箱非线性控制方法，齿轮在不同频率和不同转速干扰条件下，齿轮输出的动态误差较小。非线性控制系统能够根据外界环境的变化做出自适应调整，从而使齿轮箱振动幅度降低，效果较好。

4 结论

本文采用非线性控制方法设计了直齿控制系统，并对控制系统在不同干扰条件下的动态误差进行仿真，主要结论如下：①传统的直齿轮控制系统大多采用线性化，不能很好地对齿轮传动输出的动态误差进行补偿，通过设计非线性控制系统，采用模型反演与前馈控制对动态误差进行消除，提高了齿轮传动精度。②直齿在受到频率和转速干扰条件下，采用线性控制方法，输出的动态误差变化幅度较大，齿轮箱振动幅度较大；而采用非线性控制方法，输出的动态误差变化幅度较小，齿轮箱振动较小。③采用Matlab软件对直齿非线性控制方法输出的动态误差进行仿真验证，能够进一步验证非线性控制方法的稳定性，为科研人员提供参考数据。