基于ANSYS模态应变能法驱动轮过渡阻尼减振结构参数优化

燕碧娟，刘 威，宋 勇，王 军

（太原科技大学机械工程学院，山西太原030024）

为了减小工程机械的振动和噪声，工程上常采取的措施是采用黏弹性材料构造约束阻尼结构。具体做法是在车体结构上敷设一层具有高阻尼的黏弹性材料，然后在黏弹性材料上附加一层弹性材料（通常为金属）作为约束层，形成被动约束阻尼结构［1］。这种结构构造简单，使用方便，在工程实际应用中十分广泛。然而，传统的约束阻尼结构在实际工程应用中的减振效果常会受到一定程度的限制。对此，Whitter等［2］首次提出“Stand-off Layer”的概念，将传统的被动约束阻尼结构的基层和黏弹层之间增加一层过渡层或间隔层，过渡层的敷设可以增加黏弹层到结构中性面的距离，因而可以增大黏弹层的剪切应变。Kumar等［3-4］和Jiao等［5］等通过局部约束过渡阻尼处理开展了一系列理论和实验研究，最终得出过渡层本身并不具备耗能能力。Mead［6］、Yellin等［7］等验证得出过渡层与黏弹层一样具有耗能属性，然而发现该结构过渡层的阻尼效果难以量化。

目前大部分已有的复合材料阻尼模型是建立在黏弹性基础之上，广泛使用了应变能量法［8-9］。张少辉等［10］则在有限元软件ANSYS的基础上，从模态应变能分析的角度，由单向复合材料的损耗因子通过编程计算求得了结构的模态损耗因子，此外还比较了三维应力分量对阻尼的贡献大小。

在结构参数优化方面，为避免对目标函数值的直接优化，石慧荣等［11］则以前两阶模态损耗因子和引入约束阻尼材料总质量比为目标，建立了多目标函数。采用遗传算法的参与适应度对其进行评优化设计，但其却只能根据实际情况选择比较满意的最优解，并不能得出全局最优解。为解决此问题，李治多等［12］利用线性加权法，基于α-方法的权重因子将多工况优化问题经加权处理后，以单目标函数为优化目标进行优化设计。袁维东等［13］则选取结构前3阶多模态为优化目标对象，提出了低阶模态有一定侧重的权重值，并求取了结构的全域最优解。

综上所述，本研究将四层驱动轮过渡阻尼减振结构应用在履带式工程机械的驱动轮上（见图1），并提出了两种驱动轮过渡阻尼减振结构。通过ANSYS进行模态分析，求取三维应力、应变，计算分析驱动轮过渡阻尼减振结构的阻尼层耗能占总耗能的比率，并应用模态应变能法求取3阶模态损耗因子，对比分析确定了该减振结构中阻尼层与过渡层敷设位置。此外，以结构前3阶多模态为优化目标，通过ANSYS 1阶优化，在满足过渡阻尼管状减振结的过渡层与阻尼层最大应力、应变（Gmax、σmax）为约束条件下得出优化设计参数。最后通过谐响应分析，对优化前后四层管状过渡阻尼减振结构的最大应力、最大应变进一步验证分析，为该结构在驱动轮减振结构应用上提供一定的参考。

图1 驱动轮减振结构示意图Fig.1 Driving wheel damping structure diagram

1 减振结构建模

1.1 模态应变能法

为确定驱动轮过渡阻尼减振结构中阻尼层与过渡层相对最佳位置，可将减振结构分为方案1、方案2两种。方案1如图2所示，其中方案2交换了过渡层和阻尼层的位置。本文建立有限元参数化模型时，将结构划分为N个有限元单元，则可配置驱动轮过渡阻尼减振结构的单元为N个，其中，结构中基层、约束层、阻尼层及过渡层各自可配置单元个数为m、n、p、q。

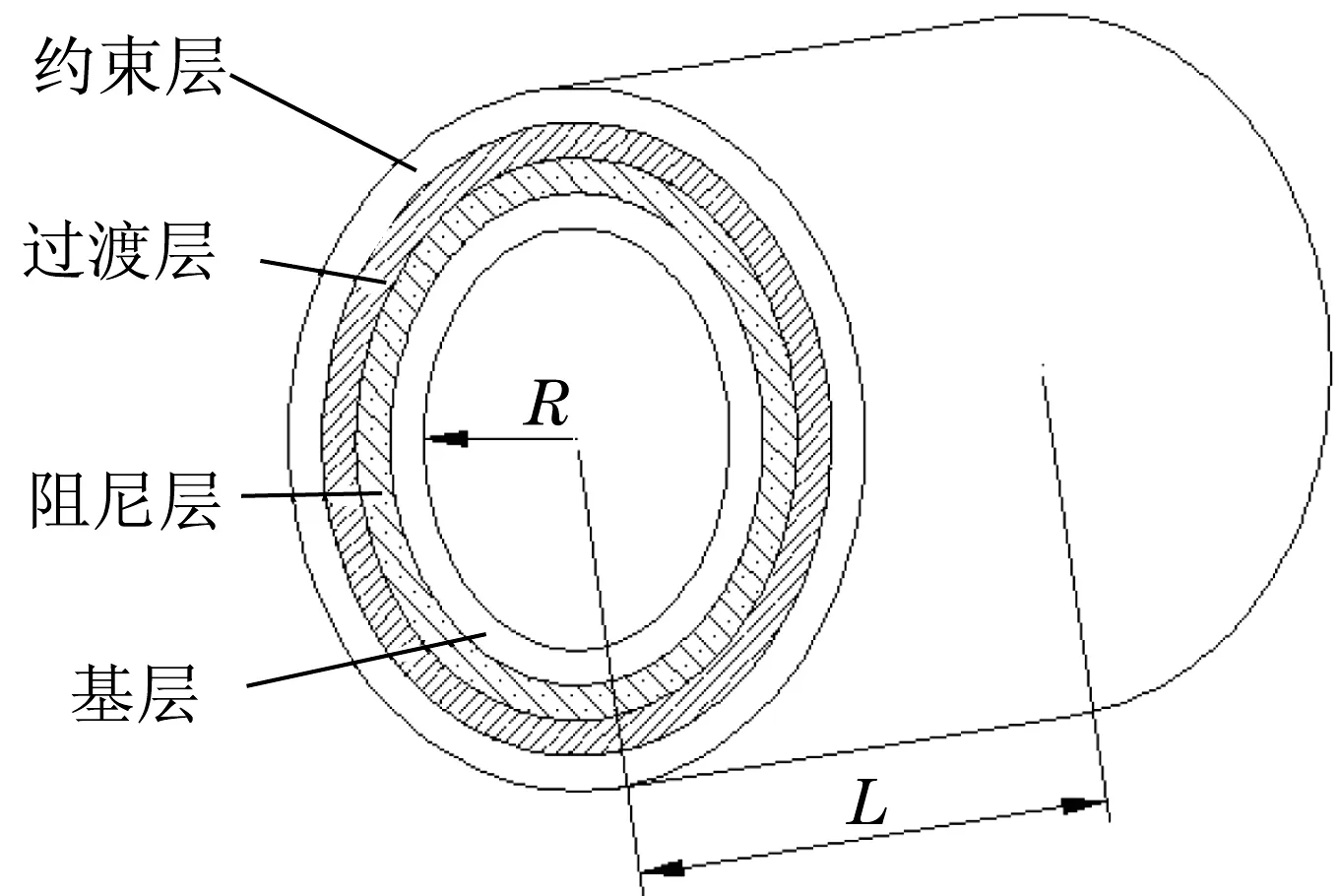
图2 过渡阻尼管状减振结构示意（方案1）Fig.2 Schematic diagram of driving wheel transitional damping structure（plan 1）

基于模态应变能法［14］，驱动轮过渡阻尼减振结构第r阶总模态应变能为

式中：［K］为驱动轮过渡阻尼减振结构的刚度矩阵；b、c、s、v分别为基层、约束层、过渡层、阻尼层；｛φ｝驱动轮过渡阻尼减振结构的实模态向量。

驱动轮过渡阻尼减振结构在振动时的第r阶模态结构损耗因子表达式可写成

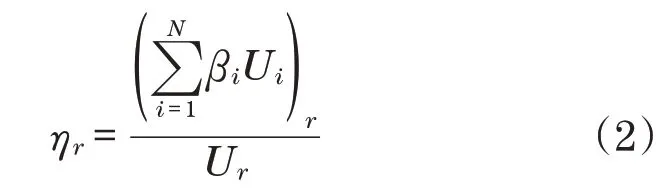
式中：βi为第i个单元的材料损耗因子；Ui为第i个单元的变形能；βiΔUi为第i个单元的损耗能量。

驱动轮过渡阻尼减振结构的所有单元，在各个方向上的弹性能来源于对应方向的应力-应变的关系［10］如下：

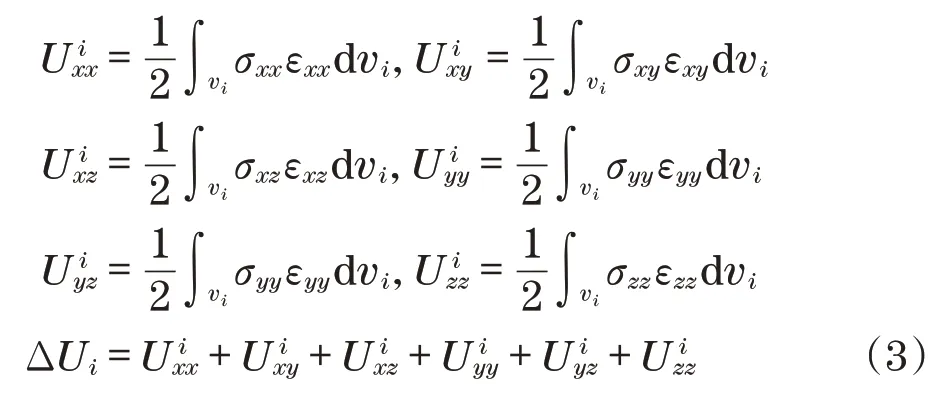
式中：为第i个单元jk方向的弹性能；σjk、εjk为对应i单元各个方向上的应力和应变分量（j=｛x，y，z｝，k=｛x，y，z｝）；ΔUi为第i个单元的总弹性能；vi为第i个单元的体积。

由式（1）~式（3）可计算出驱动轮减振结构各阶模态各部分弹性能，由此可得第r阶模态结构损耗因子为

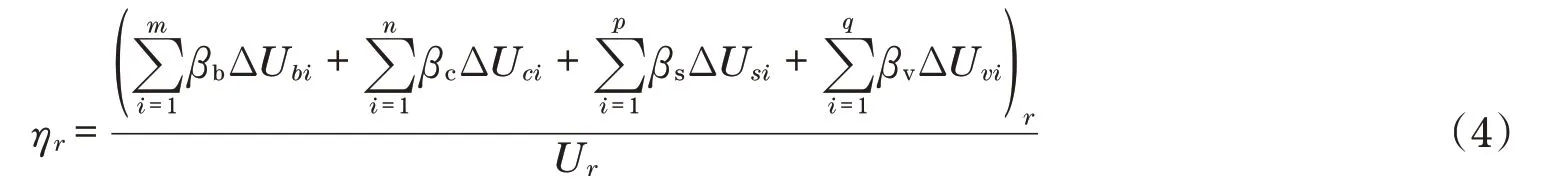
本文将基层和约束层设为金属材料，视为不可压缩，即忽略两层在厚度方向的变形能，由式（4）可得

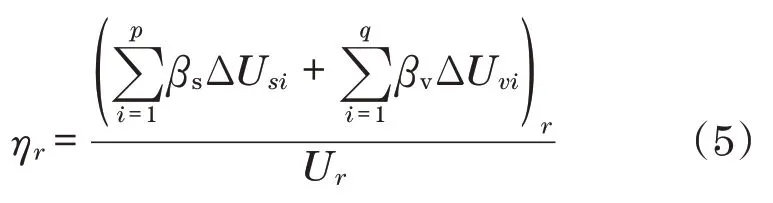
1.2 参数化建模

以某型386 k W履带式推土机减振驱动轮的内轮上减振结构为对象。在ANSYS参数化建模中网格划分时，为保证得到精确收敛且最接近实际结果的解，对尺寸变化的层间结构采用分层线划分单元法，同时应保证划分得到的结点均匀分布在指定路径上［15］。建立结构有限元模型，选取Solid185单元模拟基层和约束层，选取Solid186单元来代替阻尼层和过渡层。具体结构参数如表1所示，其中，R=0.050 m，L=0.150 m。

表1 减振结构参数Tab.1 Parameters of the damping structure

由图1可知，驱动轮过渡阻尼减振结构与驱动轮内轮凸牙为过盈配合，与其外轮圆柱孔为过渡配合，即结构基层自由度被限定，对内金属圈基层内表面施加三向固定约束，则仅在结构的基层内圆周表面施加位移全约束。

2 ANSYS模态分析

将方案1、方案2结构边界条件一致处理，模态分析方法［16］皆采用分块Lanczos法，提取结构前3阶模态应变能，并计算出阻尼层与渡层分别损耗的能量及各阶模态结构损耗因子。

由图3和图4可知：两种结构模态分析阶数为1阶时，位移振型变化一致，无明显变化；在2阶时，两种结构出现轴向单侧凸起变形。当模态处于第3阶时，两种结构位移振型都呈轴向双侧扭转振动变形；针对驱动轮过渡阻尼减振结构最大变形量，最大变形量皆发生在阻尼层，且方案2结构前两阶模态最大变形量略高于方案1结构，第3阶模态时方案1最大变形量是方案2的2倍。通过表2得出，方案1第1阶模态驱动轮过渡阻尼减振结构的阻尼层耗能占总耗能的98.65%，方案2所占比率为96.35%；方案1第2阶模态驱动轮过渡阻尼减振结构的阻尼层耗能占总耗能的98.23%，方案2所占比率为86.48%；第3阶模态驱动轮过渡阻尼减振结构的阻尼层耗能占总耗能的86.65%，方案2所占比率为97.15%。由此可知前3阶模态驱动轮过渡阻尼减振结构主要耗能以阻尼层耗能为主，但前两阶模态方案1结构的阻尼层耗能更加明显，而在第3阶模态时相反；比较两种减振结构前3阶模态的结构损耗因子，方案1则都明显大于方案2。结果表明，方案1的减振结构能使驱动轮过渡阻尼减振结构可以耗散更多的能量。同时能小幅度减小低频段的共振频率，增加高频段的共振频率，且能大幅度增大损耗因子，增加其减振作用。

图3 方案1结构阻尼层+过渡层模态位移云图Fig.3 Modal displacement cloud diagram of the damping layer+ transition layer of the structure of plan 1

图4 方案2结构阻尼层+过渡层模态位移云图Fig.4 Modal displacement cloud diagram of the damping layer+transition layer of the structure of plan 2

表2 方案1和方案2结构模态损耗因子分析对比Tab.2 Analysis and comparison of modal loss factors for schemes 1 and 2 structures

3 结构优化

3.1 优化设计

从中选取方案1进行优化，将过渡阻尼管状减振结的基层、阻尼层、过渡层及约束层厚度编号集合分别为H=｛H1，H2，H3，H4｝，阻尼层与过渡层弹性模量和材料损耗因子编号集合分别为E=｛E1，E2｝、β=｛β1，β2｝，并以此为设计变量。在ANSYS中依据图2实体模型，并赋予设计变量初值，结构参数如表1所示。以过渡阻尼管状减振结构的过渡层与阻尼层最大应力、应变（Gmax、σmax）为约束条件，致使结构发生较大的特性改变。此外，本文以加权法将多目标优化转化为单目标优化，优化目标为结构前3阶模态损耗因子，由文献［12］选取结构实际应用时低阶模态的主导地位，即权重比值为（3∶1∶1）。

因此，可以将驱动轮过渡阻尼减振结构的最优配置问题总结为

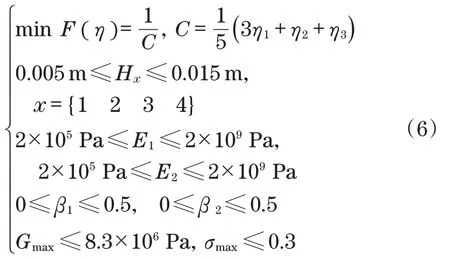
3.2 ANSYS优化

本文通过ANSYS单节工具栏Toolbar上的按钮OPTC，从而对驱动轮过渡阻尼减振结构参数进行优化处理［17］。由于优化过程中设计变量较多，相比于零阶优化而言，本文选择更为精确的1阶优化方法，对其设定迭代次数。待优化完成后，通过命令/OPLIST，ALL命令可以查看优化结果。

待优化结束后，通过软件Origin与ANSYS的接口，完成绘制优化过程中目标函数及设计变量对迭代步数的迭代曲线，从中可得出驱动轮过渡阻尼减振结构参数优化的最优解，如图5所示。此外，还可验证各组迭代数据是否满足过渡层与阻尼层最大应力、应变（Gmax、σmax）为约束条件，如图6所示。

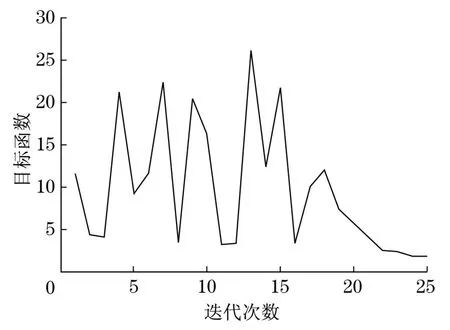
图5 目标函数优化迭代曲线Fig.5 Objective function optimization iteration curve

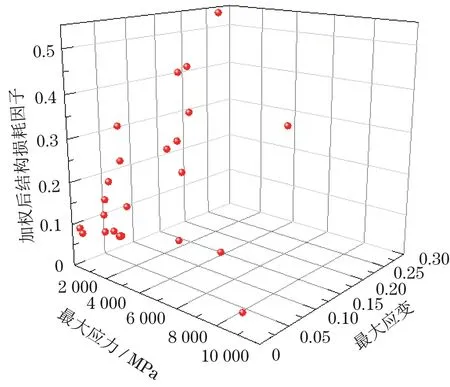
图6 约束条件迭代Fig.6 Constr aint iteration

从结果中可知，在第24次迭代时出现了最优解，最优解目标函数F（η）=1.842，即加权后损耗因子η为0.542 89，结构参数H=｛0.010 52，0.011 15，0.005 11，0.006 81｝m，E=｛8.53×106，2.11×108｝Pa，β=｛0.442 13，0.327 46｝。

对比可知，优化后驱动轮过渡阻尼减振结构的基层、阻尼层厚度都略有增加，过渡层厚度则减少了0.004 89 m，占驱动轮过渡阻尼减振结构优化前过渡层厚度的48.9%；优化后减振结构中的阻尼层与过渡层的弹性模量相差约2个数量级，且阻尼层与基层（约束层）的弹性模量相差约5个数量级；阻尼层材料损耗因子则需大于过渡层材料损耗因子。

结果表明，对各层结构取适当厚度，使驱动轮过渡阻尼减振结构耗散更多的能量，同时也验证了模态分析时方案1减振效果更好。

4 结果对比分析

对比表2中的方案1和表3，得出优化后第1阶模态损耗因子从0.29增加到了0.54，第2阶模态损耗因子从0.14增加到了0.40，第3阶模态损耗因子从0.42增加到了0.69，都明显大于优化前。结果验证了优化后的减振结构能大幅度增大阻尼层的剪切应变，使驱动轮过渡阻尼减振结构可以耗散更多的能量。

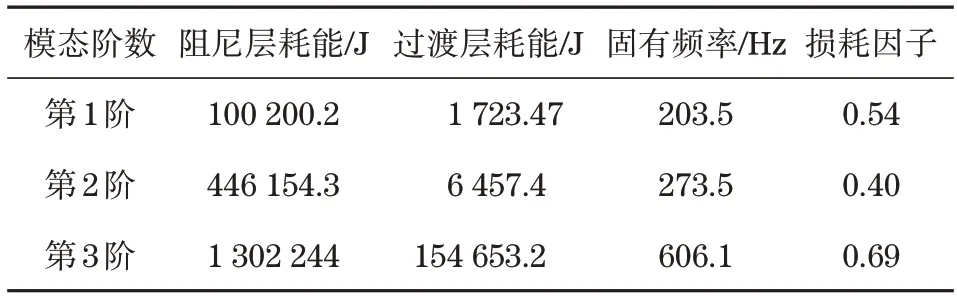
表3 优化后结构模态损耗因子分析Tab.3 Analysis of modal loss factor of structure after optimization

5 结论

本文提出了两种驱动轮过渡阻尼减振结构，通过ANSYS进行模态分析，基于模态应变能法，求取三维应力、应变，计算分析驱动轮过渡阻尼减振结构前3阶模态的阻尼层耗能占总耗能的比率和损耗因子，确定了该减振结构中阻尼层与过渡层相对最佳敷设位置；并以结构前3阶多模态为优化目标，采用ANSYS 1阶优化，在满足驱动轮过渡阻尼减振结构的过渡层与阻尼层最大应力、应变（Gmax、σmax）约束条件下，得出优化设计参数，结论如下：①前3阶驱动轮过渡阻尼减振结构主要耗能以阻尼层耗能为主，且方案1与方案2相比较，将过渡层敷设于过渡层与基层之间减振效果更明显。②优化后驱动轮过渡阻尼减振结构的基层、阻尼层都略有增加，过渡层厚度则减少了0.004 89 m，占驱动轮过渡阻尼减振结构优化前过渡层厚度的48.9%；优化后减振结构中的阻尼层与过渡层的弹性模量相差约2个数量级，且阻尼层与基层（约束层）的弹性模量相差约5个数量级；阻尼层材料损耗因子则需大于过渡层材料损耗因子。③优化后结构能减少结构变形，增大结构的剪切应变，同时，放大阻尼层的耗能作用。