罗伯特·勒·里科莱空间结构模型中的创新方法和悖论思想

葛洋康

李旭

岳文灿

引言

罗伯特·勒·里科莱（1894—1977，图1），法国工程师，提出探索“零重量和无限跨度”（Zero Weight and Infinite Span）结构构造的构想，被认为是空间结构原理的创造者之一。

1912 年，里科莱就读法国著名的索邦大学（Sorbonne University）；并在1935 年发明了一种源于贝壳的轻金属结构“抗压波纹板”（Corrugated Stress Skins）和Isoflex 刚性结构（图2），被授予了法国土木工程师学会奖章。1940 年，他首先向建筑工程领域介绍了“空间构架”（Space Frames）的概念，并在1943 年完成了Aplex[1]三维网架结构系统（图3）的设计实践。1951 年，57 岁的里科莱前往美国，先后任教于伊利诺伊、宾夕法尼亚等大学，继路易斯·康之后获得保罗·菲利普·克瑞特（Paul Philippe Cret）[2]的教席职位。1962 年他获得法国建筑学界大奖，被安德烈·马尔罗（Andre Malraux）誉为“空间结构之父”；并于1976 获得美国建筑师协会AIA 研究奖章。

里科莱和理查德·巴克敏思特·富勒（Richard Buckminster Fuller）[3]、大卫·乔治·艾默里奇（David Georges Emmerich）[4]等工程师是1960 年代空间结构研究的先驱，他们的研究成果不仅被广泛应用于建筑工程领域，而且对于新兴的结构形态学[5]领域以及建筑结构形式的创新都具有借鉴和指导意义。相对于国外，国内对于19 世纪初期西方大跨度结构发展的历史研究尚有所欠缺，对相关重要的工程师还缺少一定认知。本文主要梳理并总结了里科莱在宾夕法尼亚大学20年期间发表的关于思维方式和实验结构的研究，以期为结构设计以及建筑设计实践提供思想源泉。

一、结构创新方法

里科莱的结构创新方法主要包含了自然观察和数学逻辑两个层面。首先，在20世纪初，达西·汤普森在其著作《论生长与形态》（On Growth and Form）运用了数学中的几何学和近代新兴的力学、物理学来描述和理解生命的生长过程和形态特征；其形态学的思想逐步渗入建筑结构领域，影响了当时包括里科莱在内的众多结构巨匠。其次，里科莱早年在大学时期有关数学和物理的教育背景和液压工程师的职业经历，使他的研究展现了一种跨学科的视野。在宾大期间，他带领几批学生从物理、数学、工程学、动物学等多方面探索未来结构的新视野。他和学生建造并测试了200 多个钢结构模型，回应了他的信念——“对现象有某种认同感”和“从具体开始，慢慢向抽象靠拢”。

1.自然形态的认知

里科莱认为结构研究最好的方法就是去观察自然创造的奇迹，他研究了包括肥皂泡、蜘蛛网、蛋壳、晶体和骨骼等多种微观的现象和结构；认为自然的形态必然遵循了客观规律，它们所表现的秩序和美丽能给我们很多启示。

而“空间结构”的发明创造应当归功于自然，例如在自然界中存在了上百万年的放射线虫，那些精致的骨骼体现了空间结构的多种属性：应力表皮、三角结构、测地线、六边形网络和自同构形式……因此，自然形态在本质上就是一种结构原型，我们可以通过定义材料的属性来进行模仿和转化（图4）。

图1：罗伯特·勒·里科莱

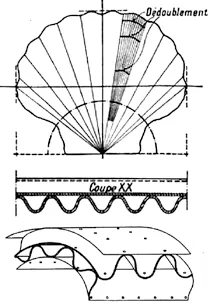
图2：抗压波纹板及Isoflex刚性结构

图3：Aplex 三维网架结构系统

2.结构模型的抽象

里科莱是将自然形态转化为结构模型的先行者。他将自然界中那些没有明确定义的现象和事物转化为抽象的结构形式，或是描述为一种抽象的数学几何关系。他采用“类比”的方法来建立具体和抽象之间的联系。类比的作用不仅在于帮助我们认知那些难以理解的自然形态，同时还可以帮助我们发现自然形态与结构模型两者在形式和结构层面潜在的相似性以及关联性。

在这里，数学的作用在于对自然形态进行简化描述，来反映事物的抽象本质；将自然形态与结构模型之间潜在的关系以一种符号化的精确方式进行表述。另外，简明的数学关系在转化为具象的结构模型的过程中可以存在多种不同的表达方式。他以多面体欧拉定理“F-E+V=2”[6]为例，阐释了“抽象”与“具体”之间辩证关系，认为数学及其符号系统蕴含了许多潜在的未开发的结构形式。

3.模型系列的推导

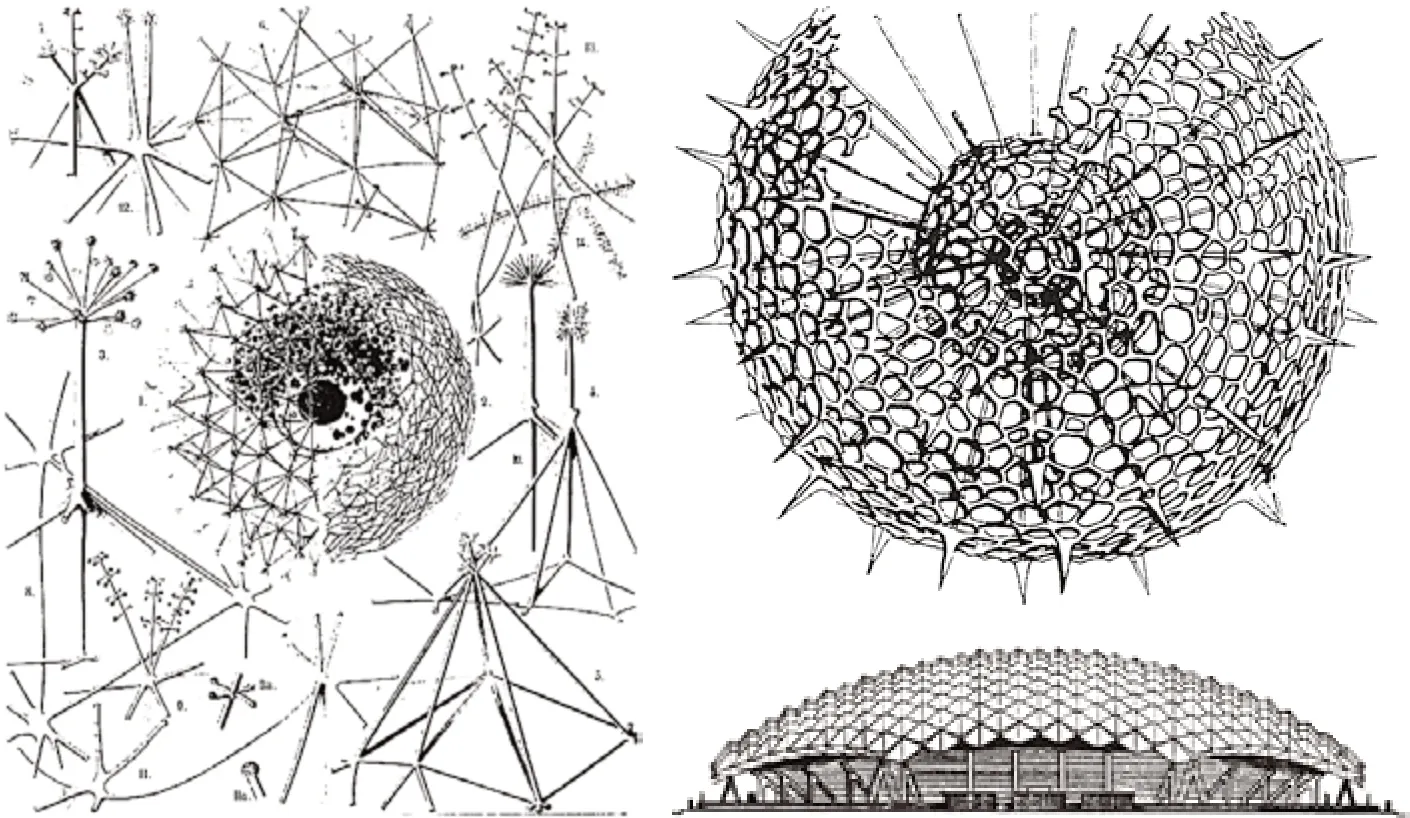
图4：自然形态的抽象与转化

里科莱将“类推”作为获得新结构形式的推理方法，这样一种方法实际上来源于拓扑学[7]。他是第一个将拓扑学应用于结构设计研究的工程师。在进行系列的推导的过程中，他维持了模型中基本的结构原理和特征关系（即拓扑属性）不变，而对系统中构件的形状和大小进行改变，从而产生一系列新的结构形式。根据相似的特征和相近的名称，他的结构模型大致可归为几个基本系列，包括空间网架结构（Spatial Truss）、索网张力结构（Tensile Cable-net）、双曲网络结构（Double Curvature Network）以及张拉整体（Tensegrity）结构等多种结构形式（表1）。

四个基本系列 表1

二、七个悖论思想

里科莱的主要影响不仅来自于他的结构创新方法，同时也来自于他在结构设计研究中形成的具有辩证主义色彩的悖论思想。他的悖论思想反映了一种矛盾的思维方式，其独创性在于将看似不相容的概念结合到悖论中，为基于自然现象的结构研究提供了深刻的见解。以下主要从现象、模型和认知三个层面展现他原创的七个悖论，同时探讨自然结构的二元性（Dualism）和自同构形式（Automorphism）等相关属性。

1.结构的艺术在于在何处开孔——环绕拉索多边形系统（FPR）

现象：人类骨骼是由孔洞构成的，孔洞的大小和分布具有随机性（图5），其存在必然是遵循了客观的自然规律。关注自然形态的孔洞，基于拓扑关系去研究孔洞的数量和形状对结构整体的影响，启示了一个看似矛盾的概念——“结构的艺术在于在何处开孔”[8]。

模型：FPR（Funicular Polygon of Revolution）模仿了宏观的骨骼形态和微观的“孔洞”概念（图6、图7），由三部分构成。1）外围的钢索是系统的受拉部分，环绕形成最小表面（Minimal Surface）[9]的空间网络。网状结构本质上是一种编织结构，相比连续的膜表面，其表面分布有很多孔洞。这样一种网状结构相比单索链系统，能够通过拉索间的相互作用消除结构系统的振动。2）中心杆件是系统轴向的受压部分；基于结构经济性考虑，它被设置在体系中心，两端与拉索相联系。3）环状的分隔片作用在于锚固钢索，能够防止网状结构发生形变；同时环状形式具有最佳的受压性能。

见解：FPR 有别于传统桁架结构，它根据不同的受力方式将结构系统分成两个部分，体现了结构二元性的思想：系统中受压力和受拉力构件采用了不同的材料及构造形式，不仅发挥了最佳的材料性能，而且减少了结构自重，利于实现更大跨度。

2.坚硬的空心绳索——空中轨道

绳索在材料和构造两个层面都展现了极大的创造潜力。一方面，纤维材料是由物质颗粒紧密结合成的线性序列，它直接影响了材料强度；另一方面，绳索（图8）可以是由多股纤维编织缠绕构成的。里科莱用“坚硬”和“空心”定义绳索，他认为在绳索中引入的纤维或连接越多，绳索的强度和刚性就越大；同时纤维的联结越紧密，系统的稳定性和承载力就越好。

图5：骨骼的孔洞

图6：FPR

图7：伪球面FPR（1962-2）

图8：纤维构成的绳子

图9：空心绳索

图10：Sky-rail

里科莱着迷于“想象进入绳子内部”，实践并制作了一系列大尺度的空心绳索结构（Hollow rope，图9）。他在系统中引入预应力，通过增加系统的整体强度来抵抗弹性形变。预应力的钢束取代了混凝土等其他重型材料；轻盈的结构形式直接表现力流的抽象本质（结构系统中力流的传递），使结构层可以做到轻薄如纸，在降低了系统自重的同时也加大了系统的跨径。

空心绳索是实践高强度管状结构的起点，其经验意义在于建立从材料到构造的联系，将一维的纤维材料拓展为交错编织二维的表面。另外，空心绳索这样一种不附加重量的结构，其潜力在于发展为一种新型的铁路隧道Sky-rail（图10）。Sky-rail构想了一种超长跨度的高架交通系统，其结构通透的属性使人们可以在空中俯瞰城市形态，保持对城市整体方向感的认知。

3.方式越多，使用越少——三轴六边形测地线穹顶

放射线虫（Radiolaria）精致的骨骼（ 图11） 是 由 三 角 结 构（Triangulated Structure）组成的应力表皮（Stress Skin），它所遵循的三个轴向的六边形空间几何网络反映了测地线[10]的特性。

现代的城市规划布局以正交网络为基础的，这是由古埃及对于直角的利用而创造的几何秩序。在维奥莱-勒-杜克（Viollet-Le-Duc）结构理性主义的影响下，里科莱认为未来城市空间的划分在于建造“通道结构”而不是房屋，人们需要一个高效的系统让城市空间进行交互，并形成距离更短、速率更快的空间交互网络；而其先决条件在于建构一种快速通道，并将潜在的通道依据交叉点最少的原则进行组织。

三轴六边形穹顶（Trihex Dome，图12）模仿了放射线虫的骨骼形态，是半规则的几何构成（包含了三角形和六边形）。它被认为是一个很好的理论样板：其网络结构在微观层面有着应力分布的合理性；而在宏观层面则探索了可能改变城市本质和人类流动的新方式，表现了地球表面快速通道的一种组织模式。

将三轴六边形穹顶的三轴网络与正交网络进行拓扑比较分析可以得出：在相同节点距离和面积范围内，三轴网络（图13）相比于正交网络，交叉点少约18%，通道总长少约13.5%，可减少大量时间成本，即单位时间的通勤效率更高。这反映了“控制论”（Cybernetics）[11]的一个定律，即“方式越多，我们需要使用的就越少”[12]。

4. 破坏的秩序遵照建造的秩序——Isoflex 管

贝壳具有很强的抗压性能，能够很好地应对水流的冲击。从形式而言，贝壳凹凸起伏的表面具有自同构形式（Automorphic Form），即像正弦曲线一样不断周期性地自我重复的形式；这种褶皱的形式能够很好地提升惯性矩[13]，增加截面抵抗弯曲的性能。

里科莱受贝壳启发，发明了波纹金属板，以及由上下两片波纹金属板交叉叠加而成的Isoflex 刚性结构。为了解决钢管应用于精密光学仪器时存在的振动问题，他在“谐波”中寻找分解振动的方式，认为Isoflex 的自同构形式同样适用于钢管（图14），由此设计了一种新的稳定性结构Isoflex 钢管（图15）。这个结构系统由许多根“基波”状的自同构形钢管（Automorphic Tube）构成，这些轴向的承重的钢管被划分为多个“谐波”段，并与三角细分的格构体系叠加形成整体。

图11：放射线虫

图12：三轴六边形穹顶

图13：三轴网络（球面）

图14：Isoflex应用于钢管

图15：Isoflex 钢管

图16：受压屈服后的Isoflex 钢管[8]

Isoflex 钢管中存在许多四面体结构（Tetrahedra）和四方锥结构（Square-Based Pyramid），使整个系统在受轴向压力下的失效过程中一直能够保持最大的截面进行工作；此外系统中的钢管屈服点都出现在“谐波”的凹凸顶点处，且屈服长度与“谐波”长度相吻合（图16）；这种与“谐波”对应的屈服反映了一个基于认识论的结论——“系统的破坏顺序应该遵循它的构造顺序”。

5.图景中的幻象——“猴子鞍”

肥皂泡膜（图17）被称为最小表面或经济表面（Surface of Economy），是自然界中出色的薄膜结构，它展现了自然结构惊人的严谨和美感。事实上，液态的气泡薄膜本质上是一种分子不断移动的引力现象，它几乎不存在物理实体；不稳定的状态使其呈现幻象一般的图景。

里科莱研究了许多有关肥皂泡膜的结构，“猴子鞍”装置（图18）就是其中之一。“猴子鞍”的双曲表面可以通过将扭曲后的六角形框架浸入肥皂溶液中得到。而实验模型上的曲面薄膜构造则通常需要对绳索进行系统性的编织配置来进行模拟。“猴子鞍”装置的薄膜表面有三个波峰和三个波谷，他的水平投影是正六边形的，这个薄膜的曲率从中心到波峰/波谷逐渐由零变大，膜表面也从水平面逐渐过渡到竖直平面。

六边形的预应力膜表面由三个轴向的绳索编织形成。相比于正交网络，三轴网络具有更高的绳索的利用效率。“猴子鞍”表面的预应力网络所具有的承载力（图19）也明显超出计算之外，证明了预应力构件可以吸收压力。

6.重型构件构成的轻型结构——四面体节点

现代化的工业可以生产无限长度的型材，为了满足运输条件，这些型材被分隔为小段，之后再通过连接件（图20）重新组装成整体；连接件的增加势必导致结构自重和经济成本的增加。基于对空间框架中关节的低效性的认识，里科莱认为轻型结构关键在于减少关节，即关节的数量和关节上的分枝数越少，结构系统就越轻盈。

里科莱提出了一种四面体形的连接件（图21）来代替关节，四面体的每个顶点上的关节简化为一个简单的环，用以连接重型构件；它通过摩擦力与重型杆件之间保持结构整体的稳定性。这种构件遵循了连续性原则，保持了重型构件杆件受力的连续性和完整性（图22）。

事实上，里科莱曾认为建筑的艺术是用火柴棍建造，轻型的结构必须使用轻盈的组件，因为大量轻质构件组成的整体会是轻盈的。而现实证明短长度构件需要大量的连接，这只能增加结构冗余的重量，因此他认为轻型结构需要的是三维空间结构中少量的重型构件，即“制造轻型结构的艺术是由大而重的构件完成的”。

图17：肥皂泡膜

图18：“猴子鞍”

图19：结构试验中的“猴子鞍”

图20：桁架结构的关节

图21：四面体连接件

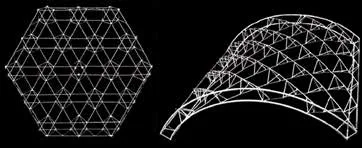
图22：重型构件网络

图23：芬克桁架，1875年

图24：双柱桁架

图25：Polyten桁架系统

7. 悬置在空中的柱子——双柱桁架（Polyten 桁架系统）

桁架的作用规则在于对抗弯矩，传统的桁架主要使用同一种材料的杆件承受轴向拉力或压力，并未根据不同的受力方式对材料进行区分。

19 世纪源于美国铁路工程的芬克桁架（Fink truss，图23），利用钢索创造了“虚拟的支撑”，造就了柱子悬置在空中的神奇景象，这反映了前辈工程师在结构艺术上的独创性。

里 科 莱 的 双 柱 桁 架（Queen Post，图24）借鉴了芬克桁架，区分了张力和压力构件，将上部杆件的压缩以及底部钢索的拉伸协同运作，抵消了弯曲形变；在发挥系统中不同材料的性能的同时，实现了结构重量的最小化；而三段式构成方式相比芬克桁架，实现了更大跨径。

事实上，双柱桁架是里科莱众多结构模型中的一个基本原型，或者说是“原始细胞”[14]，基于其“二元性”的原理可以转化出一系列不同形式的结构构型。例如Polyten 桁架系统（图25）由多组双柱桁架构成，其具有重复性的优雅形式也体现了自然界中自同构形式的原则。

三、影响和意义

里科莱的七个悖论思想源于对自然现象和模型实验的辩证认识；他的悖论思想是对模型的注解，两者互为补充、密不可分。

他的模型和悖论思想对于结构设计领域有着最为直接的影响。其结构模型（包括空间网架结构）作为先验的结构形式，被工程师应用于当代大跨度的结构设计当中；其研究被认为是具有创造性的范例。他将模型作为一种概念性装置用于修饰结构设计，将设计的活力注入结构研究领域。事实上，他的Isoflex 钢管被设计应用于军事领域的潜望镜装置，用于解决颤动对光学设备的影响；而他的抗压波纹板被应用于早期飞机机身外壳的设计。

里科莱对于建筑领域的影响是相对间接的，他的悖论思想和结构模型对于当代建筑的学科发展的意义是有待拓展讨论和深入挖掘的。在这一点上，一些建筑师起到了很好的示范作用，并在他们的建筑设计实践中给出了线索和启示。

以路易斯·康为例，他在耶鲁大学美术馆等诸多案例中，采用塑性混凝土表现了空间结构。在形式层面，最为典型的是费城城市之塔（图26），建筑在整体结构、楼板的构造等多个层次应用了由四面体单元构成的空间网架结构，而四面体结构单元正是来源于里科莱 对于放射线虫（见图4）的研究。思想层面上，路易斯·康本人将其思想总结为“空心石头”（Hollow Stone），“空心石头”成为康建筑中不可或缺的元素。“空心石头”代表了用于容纳机电管道设备的建筑结构（包括“空心柱”和“空心梁”），康在主观上将空心结构作为“服务空间”与建筑中的“被服务空间”进行区分。康的空心结构与里科莱的“结构的艺术在于在何处开孔”和“固体掏空”（Hollowing the Solid）的悖论思想如出一辙。

伊东丰雄的仙台媒体中心（图27）则代表了建筑结构的历史性突破。建筑融合了柯布西耶的多米诺体系（Dom-Ino）以及里科莱的“坚硬的空心绳索”，草图上的金属网状结构被描述为“自由舞动的海草”。此外，伊东的一系列高层建筑，包括TOD’s 表参道大楼、MIKIMOTO Ginza2（图28、图29）都采用了装饰化的结构表皮，将结构形式与建筑开口形式结合，反映了里科莱的“结构的艺术在于在何处开洞”的基本观点。在岐阜媒体中心，他采用了源自于测地线穹顶的三轴网络，相比于两轴网络，三轴网络在三维曲面结构上具有更好的整体性能（图30）。

图26：费城城市之塔，路易斯·康

图27：仙台媒体中心，伊东丰雄

图28：TOD’s表参道大楼，伊东丰雄

图29：MIKIMOTO Ginza2，伊东丰雄

图30：岐阜媒体中心的三轴网络，伊东丰雄

四、结语

随着新材料和新技术的不断发展，结构形态的创新为现代建筑创作指明了一个富于生命力的发展方向：突出强调建筑结构表现和建造理性的设计倾向是当代建筑设计中的重要方向，通过结构构思推动建筑创作的方法也越来越受到关注。里科莱的结构模型、悖论思想以及研究方法，都可以帮助我们探索建筑学领域更多的可能性，扩充建筑理论的边界。在探索建筑未来性方面，他的“重型结构构成的轻型结构”强调连续性的力流传递，以及结构效率最大化的思想，在今天的建筑设计过程中仍具有重大意义；而张拉整体（tensergrity）将弹性材料和刚性材料结合的结构构造方式，仍然值得在设计上进行探索和研究。

注释

[1] 雅温得的车库使用了Aplex 体系，并被视为里科莱一切重要设计理念的发源。Aplex由预制木杆件和金属连接件组装而成，适用于飞机棚等大跨度的空间类型，这种结构不仅节约材料和人工成本，而且构件轻盈易于装配。

[2] 保罗·菲利普·克 端（Paul Philippe Cret，1876—1945），宾夕法尼亚大学教授，是路易斯·康、林徽因等著名建筑师的老师。

[3] 理查德·巴克敏斯特·富勒（Richard Buckminster Fuller，1895—1983），美国国家设计院院士，是早期从事结构形态研究的代表人物之一，发明并推广了测地线穹顶——1967 年此结构被用于蒙特利尔国际博览会的美国馆。

[4] 大卫·乔治·艾默里奇（David Georges Emmerich，1925—1996），法国建筑师，工程师；法国结构形态学（ Structural Morphology）领域专家，从事轻型结构等相关研究。

[5] 同[1]。

[6] 多面体欧拉定理是指对于简单多面体，其各维对象数总满足一定的数学关系。在三维空间中，多面体欧拉定理可表示为：“F-E+V=2”（表面数-棱长数+顶点数=2）

[7] 拓扑学（Topology），是研究几何图形或空间在连续改变形状后还能保持不变的一些性质的学科。重要的拓扑性质包括连通性与紧致性。

[8] Khaled Dewidar. Robert Le Ricolais：the art of structure is where to put holes[J]. 2016，DOI：10.13140/RG.2.1.3464.5366.

[9] 物理学中，由最小化面积而得到的极小曲面的实例可以是沾了肥皂液后吹出的肥皂泡。肥皂泡的极薄的表面薄膜称为皂液膜，是满足周边空气条件和肥皂泡吹制器形状的表面积最小的表面。

[10] 测地线（Geodesic），又称大地线或短程线，可以定义为空间中两点的局域最短或最长路径。测地线的名称来自于对于地球尺寸与形状进行测定的大地测量学。

[11] 诺伯特·维纳的控制论（1948 年）是一门研究机器、生命社会中控制和通讯的一般规律的科学，是研究动态系统在变的环境条件下如何保持平衡状态或稳定状态的科学。

[12] 同[8]。

[13] 惯性矩（Moment of Inertia of an Area），即面积二次距，也称面积惯性矩，是一个几何量，通常被用作描述截面抵抗弯曲的性质。惯性矩的国际单位为（m4）。

[14] 结构研究中存在两种观点：一种是运用加法，组织像细胞一样的重复性构件；另一种是运用减法，削减体块达到最终的结构形态。