图解静力学：一种实现强结构的操作方法

[德]托尼·科特尼克 文

王帅中 译

曹婷 校

一、前言

近年来，图解静力学（Graphic statics）在结构设计中出现了复兴[1]。图解静力学，一种基于矢量的对结构中力的平衡状态的塑造，在卡尔·库尔曼（Karl Culmann）于1866 年出版的《建筑结构设计》（Die Grafische Statik）一书中就被正式确定为建筑结构设计的方法论。库尔曼的成果不仅为结构分析提供了科学基础，而且直到20 世纪初还被应用于世界土木工程师的教育[2]。静力学问题的几何分析标志着科学的建造方法的开端。

但是工程学科学化程度的不断提高很快导致了几何方法被现代数学的解析与代数方法所取代[3]。这种转变对工程知识的发展产生了巨大的影响，同时也加深了建筑学与工程学之间的差别[4]。早在20 世纪50 年代，皮埃尔·路易吉·奈尔维（Pier Luigi Nervi）就指出，这种对建筑结构的解析与代数化的理解与设计过程的相关性有限，因为“在设计的成形阶段，结构理论并不适用于这一全面确定其主要特征、品质和缺陷的过程中，而必须要借助直觉和示意性（schematic）的简化”[5]。

在迈入千禧年之际，一些大学如美国的麻省理工学院（MIT）或瑞士的苏黎世联邦理工大学（ETH Zürich）和洛桑联邦理工学院（EPFL）等，在建筑师教育中恢复了图解静力学来“试图为建筑师开发一门真正的静力学课程，而不是简化训练工程师的传统方法”[6]，旨在促进建筑与工程之间更具合作性和创造性的互动。

这一课程改革的动机不仅是图解静力学的直观性和可视性。图解静力学基于矢量的操作所具有的塑造性（constructive）和生成性（generative）的特点，还可以与21 世纪初开始在建筑中出现的数字化设计方法方便地进行衔接[7]。但最重要的是，图解静力学有利于以设计为导向的、对建筑结构内力的理解，是一种对三维空间中力的分布模式（pattern）的主动设计参与。正是图解静力学的这种近乎是图解的特征（diagrammatic character），支持了结构思维与建筑概念的融合，从而支持了强结构（Strong Structures）的理念[8]。本文着重从后者将图解静力学作为一种建筑设计方法的角度，阐述了结构设计思想的关键要素及其在众多项目中的意义。

二、力的分布

图解静力学与实现力的平衡的组织模式相关。换言之，建筑结构可以被视为一个子系统（subsystem），用来操控由施加在建筑物上的荷载引起的内力在空间中的分布（图1）。这种力的分布是通过重复使用两种基本操作来实现的：将两个力合并为一个或将一个力拆分为两个。基于力的平衡条件，这些操作总会造成力在方向上的变化。在图解静力学中，最基本的力的分布模式是悬链形的索以及它的对偶形式——拱（图1c）。这一众所周知的事实早在17 世纪就被罗伯特·胡克所描述过[9]。1889 年，安东尼奥·高迪（Antonio Gaudi）为巴塞罗那的圣家族大教堂（Sagrada Familia）制作的著名的悬链模型中就利用了它作为设计的工具，后来海因茨·伊斯勒（Heinz Isler）又将其拓展为挂布模型来设计混凝土壳体[10]。

通过重新引导力的方向来逐步塑造空间中力的分布是图解静力学的基础，同时也是其作为建筑设计方法的核心。它导致了结构设计思维的转变：不再是对结构性能明确的如柱、梁和板等预定义元素进行组合，而是对空间中的力流进行塑造，从而在暗含的建筑概念的指导下寻求结构的平衡。这种在常见的结构元素及其固定的类型之外来探索平衡的方式，为创造性的和非常规的解决方案敞开了大门，就像OOPEAA 建筑事务所在芬兰凯尔赛迈基（Kärsämäki）的小教堂的设计中所展示的那样（图2）。

教堂位于芬兰中部小镇凯尔赛迈基郊外的一处河岸上。从外观上看，这座建筑是一个简单的、抽象的体量。它没有明显的开口，完全被浸有柏油的手工木瓦的黑色外墙所覆盖，只在体量的一角有一个切口在暗示入口位置。这使得建筑具有了整体性，并与周围的自然环境形成鲜明的对比。由此产生的“例外”又并非异样的表达方式，通过对围绕在建筑四周的阴影线进一步强调，使建筑体量似乎悬浮在地面之上。

步入建筑，一条坡道通向前厅，人们可以从前厅的北角进入教堂。教堂的空间本身是古朴的，有一个带有陡峭的脊形屋顶的木制隔间（图2c）。光线通过一个灯笼状的天窗从上方进入空间。然而，普通的木结构屋顶被集中的支撑结构所取代。它漂浮在游客的头顶上方，将屋顶的荷载沿着如索（的结构功能）一般的木质杆件对称地传递到教堂空间的墙壁上（图2d）。为了将这一漂浮的支撑系统的内力保持在较小值，同时实现结构构件纤细的尺寸，屋顶的部分重力荷载被从屋面顶部悬挂着的木瓦外墙所抵消，起到了类似配重的作用（图2e）。因此，外墙像一件衣服一样包裹着教堂，保持教堂内部不受周边环境的影响，同时，教堂空间与外部空间之间的中间空间也为教堂空间提供服务性功能（图2a）。

因此，屋顶的荷载被同时分配到教堂空间的内部和外部，从而在会众空间的墙壁之上形成了一个平衡的结构。屋顶结构的设计表明，图解静力学是一种对内力及其在空间中的分布的思考。这种想法并不支持对传统建筑元素的标准化利用。其塑造的力的分布模式更像是引导了一个独特的、铰接的建筑结构的生成。在教堂的案例中，会众空间的承重结构被建造成带有凹角缝的巨大原木结构，来平衡屋顶5 英寸×5 英寸木质的轻型框架结构。由此，图解静力学促成了一种以建筑概念为导向的差异化（differentiated）结构思维，这也是强结构的基本理念。

图1：在图解静力学中，对平衡的探索是基于同时使用形图解。a）和力图解；b）来实现的。这些平面图解用几何术语描述了平衡的条件，并使得塑造力的分布成为可能，如索或拱；c），通过后续重新确定力的方向来塑造力的分布

图2：由OOPEAA于2004年完成的芬兰凯尔赛迈基教堂。该结构像一块布一样包裹着教堂空间——建筑的核心部分，从而形成了附属的空间。该设计是基于将力围绕核心空间重新定向来进行的

三、变换

在空间中重新定向和分配力不仅是图解静力学中的主要操作，同时也是其作为设计工具的操作核心。基于图解静力学的设计思维创造出的是一个处于平衡状态的压力和拉力的空间关系网（spatial network）（图2e）。该关系网代表了力之间的一组可拓展的关系，并可以通过参数变换和拓扑变换进行调整。

关系网的参数变换不会改变力之间的关联模式，而是改变力之间的相互作用的强度。这可以体现在从拱形（图3a、3b）到柱状（图3c）最后到悬挑状（图3d）的力的分布转化中。这意味着建筑结构承重性能的差异不是由荷载和支点的空间关系决定的，而是由其根本的关联模式所决定的。

通过将拓扑变化应用到现有的关系网上，可以引起关联模式的变化，如通过合并两个悬挑状的力（图3e）将力的线状平衡（图3c）转换为曲线状（图3e）。这种拓扑变换使力在空间内可以重新分布，从而使关系网中相互作用的压力和拉力发生性质上的变化。

在新加坡海湾花园中的一个临时展馆AirMesh 的设计中，这两种类型的转化方式都被明确地用作设计的主要驱动力。设计的初始体量的方向由四个向量定义，这些向量与周围景观中的凸起有关。在设计过程中，以轻盈的、可居住的结构为设想，网格化的体量成为设计的起点（图4）。根据空间中三个力可以相互抵消来达到平衡的原理，该网格被拓扑转化为一系列相邻的四面体——这个网格体也正是由基于这一原理下形成的四面体所构成的。以这种方式生成的力的分布模式，保证了足够的结构稳定性（图5a）。在第二步中，对所得的网格进行了参数化变换，以便在不同的荷载状况下调整这个力的分布模式中每个力的大小（图5b）。这两种转化方式互动反馈，最终生成了一个力流的空间关系网，并被转译为尺寸不同的杆件。在可回收的尼龙网的覆盖下，建筑呈现出瞬时的特征，如同一团团的力包裹着整个空间。

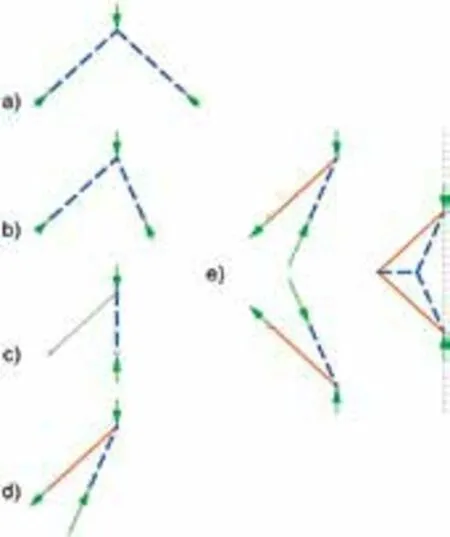
图3：一个力的分布模式从拱形（a，b）到柱状（c）到悬挑状（d）的参数变化，以及通过合并两个悬挑来重新定向力的作用线（e）

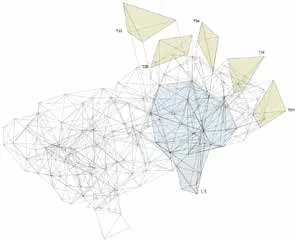
图4：AirMesh临时设施，新加坡滨海湾花园，2019年，Carlos Bañón和Félix Raspall设计。在三维中通过三个力来平衡荷载，由此产生四面体的结构布局，进而生成展馆的体积模型

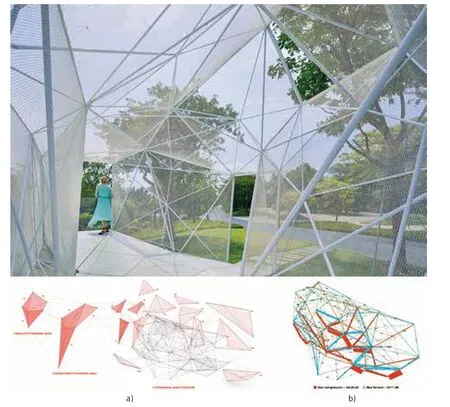
图5：AirMesh临时设施——设计基于节点从初始的网格到四面体的拓扑变换和随后的参数变换

该展馆不仅说明了两种类型的变换在设计过程中的使用方式，由此产生的结构体系也展示了一种新的建造美学——基于力在空间中的分布而产生的一种有着虚无感的激进美学。综合起来说，通过参数化和拓扑变换，可以协调荷载的传递来设计出符合设计意图的力的分布模式。因此，图解静力学须被看作是一种在物理的必要性和设计的自由性之间取得平衡的积极设计行为。

四、材料的分布

设计的自由度不仅存在于对力的分布模式的塑造中，还存在于从这种模式向结构构件的物质形态的转化中。一般来说，图解静力学是一种独立于材料的结构设计方法，其重点是力的分布。材料只需要作为力在空间中传递的媒介。

高迪和伊斯勒的历史性的应用，以及最近关于建筑设计中找形方法的讨论，似乎暗示着建筑结构的物化形状与其所传递的力之间有着非常密切的关系。在所有这些情况下，结构构件的形状被理解为它所包含的力的分布模式的最小容纳体（envelope）。以材料的屈服应力和极限应力作为参数，这种对力-形关系的诠释可以得到一个结构构件的成形过程，它在某种程度上类似于股骨的情况——基于已有的力的分布模式优化所需的材料量（图6b）。骨骼需要将身体的重量从盆骨重新传递到腿部。这些内力的重新定向会在重新定向发生的位置（力的分解点）产生较大的力，从而需要以材料的堆积应对增加的应力，因而形成了股骨的常见形状——在与大转子骨相交处加宽（图6a）[11]。

然而，将结构构件的形状定义为力流的最小容纳体其实是一个设计决策。物质化的容纳体也可以根据其他的设计标准结合已确定的力流（力的分布模式），来更自由地诠释和设计形式（图6c）。因此，塑造出的力的分布模式，需被看作是结构元素形式的图示（diagram），它并非是建筑结构的形式本身，只是为形式的设计提供了指示。

五、形——力的近似关系

股骨的例子表明，力可以在空间中多向移动。然而，这种偏离作用线的移动必须通过额外的材料积累来实现。这种设计的自由度和物理的必要性之间的关系，允许了力的分布模式的图示化应用。像在AirMesh 的节点设计中（图7），每个节点都位于所有杆件的虚拟交点的附近。这是由于所有杆件都具有一定的厚度，因而无法真正交于这一点， 只能在虚拟焦点的附近连接起来。这就会让杆件的内力沿着节点的表面产生偏移（deviation），因此会在表面上产生额外的应力，而这些应力需要在设计节点的厚度时考虑进去。

因此，受力模式和实现的形式之间可被视为一种近似的关系，一种打开了设计自由度的、弱的相关性。在AirMesh 的节点中，这种偏差于已塑造的受力模式而产生的自由性，使节点与杆件之间得以在视觉上平滑过渡，并由此形成了一个节点中相互作用的力之间的连续性美学。

力的偏移（力相对于初始作用线的偏移）带来的设计自由度也是维也纳应用艺术大学扎哈·哈迪德（Zaha Hadid）的设计课程在2011 年进行的一系列探索的出发点。在这些探索中，形式生成的算法过程与弗雷·奥托（Frei Otto）、菲利克斯·坎德拉（Felix Candela）或海因茨·伊斯勒（Heinz Isler）的开创性工作联系在一起，他们实现了 “基于结构材料的找形过程中最优雅的设计”。“从弗雷·奥托那里我们可以了解到，我们所渴望的形式和空间的丰富性、有机连贯性和流动性是如何从错综复杂的力的平衡中合理地产生的。我们扩展了弗雷·奥托的方法来同时包含环境和结构的逻辑，我们从材料转向计算模拟。”[12]

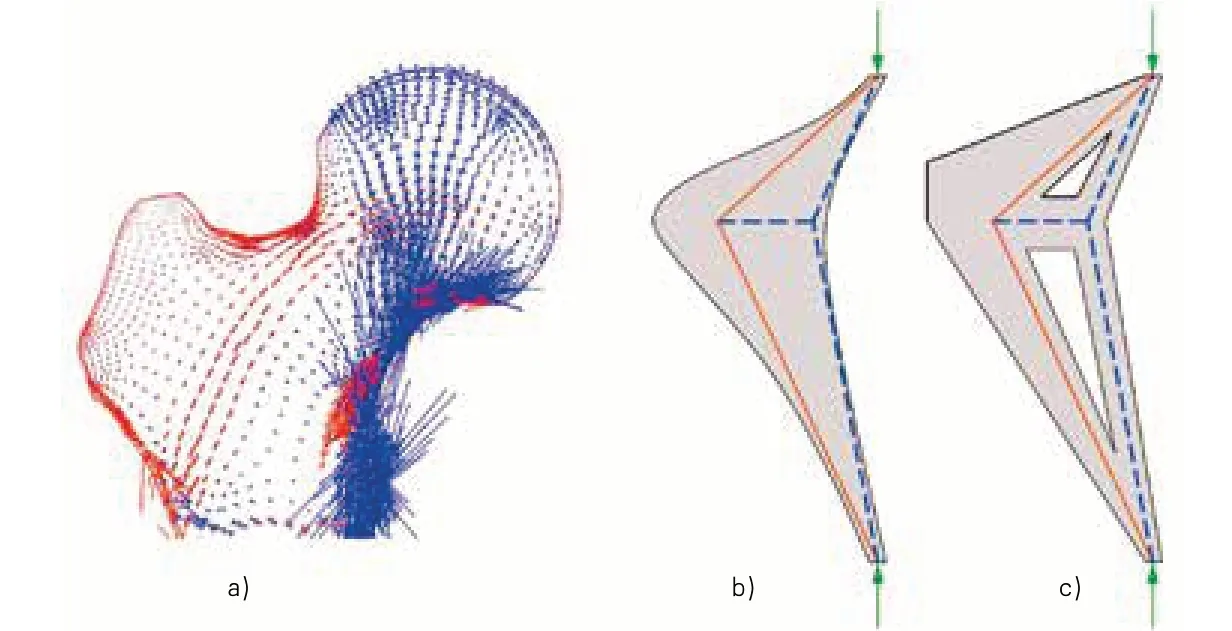
图6：与力的模式（b）的内力流近似相关的材料分布，并分别与股骨近端形状和主应力分布（a）以及基于其内力设计的容纳体（c）进行比较

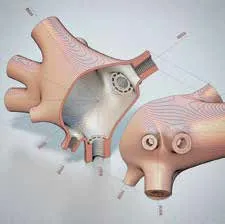
图7：AirMesh临时设施——此节点设计为3mm厚的钢壳，是为了实现杆件视觉上的连续性，其整体形态近似于最初始的力流

图8：2012年威尼斯建筑双年展上，海因茨·伊斯勒的壳体结构，以及维也纳应用艺术大学扎哈·哈迪德工作室的学生重新诠释的壳体结构的展览

这些壳体设计先驱者的设计中，形与力之间严密的关系被用来当作有控制的探索设计自由度的起点——通过从这些优化过的设计中偏离衍生而来。在2012 年威尼斯建筑双年展的一个名为“共同点”（Common Ground）的展览中，这些探索与壳体结构的先驱们的作品一起被展出（图8）。在建筑的表达策略中，这些探索所确立的通过应力的大小来调整构件尺寸的设计过程——即一种建构的策略，被扎哈·哈迪德建筑师事务所的一些后续项目所运用[13]。

六、结论

图解静力学是在主动地塑造建筑结构内部的力流，而不仅是对内力计算的视觉化呈现。更重要的是，这种几何塑造的方式促进了力在材料中分布的基本逻辑的参与，并以此为基础展现出了其作为设计方法的潜力。这种以力为导向的操作方式的特点是，能够在工程师和建筑师的观点之间以及结构的平衡和空间营造之间展开对话。这是通过对空间力流的塑造而非对预定义的结构元素的组合来实现的。这就将建筑形式拓展为结构设计内的一个话题，它利用力流的拓扑灵活性来指导空间中的物质材料的分布，是建筑形式的建构性表达。然而，之前所讨论过的例子表明，内部的力流与实现的形式之间并不存在严格的推论关系。传力模式的灵活性与其作为载体的围合材料之间的调和性，都为设计的自由度提供了可能性。这意味着，建筑结构的最终形式不能仅仅由力的物理性质来推进。结构设计是由设计的态度来推进的，这种态度位超越了物质，但又强烈地受到物质材料的影响。在这种以图解静力学为基础的设计思想中，建筑结构不仅被认为是建筑的组织骨架，同时也是建筑的肉身。结构和建筑融合在一起，正如斯维勒·费恩（Sverre Fehn）所说：“无论你是多么优秀的建筑师，如果你没有机会用结构来表达你诗意的思想，那么你就缺少了建筑的根基。结构是一种语言，是一种自我表达方式，思想和语言之间应该有一个平衡。每一个故事都有一个结构”[14]。图解静力学作为一组系列的操作方式，不仅是一种理解结构语言语法的方法，而且也是一种允许它发声的方式——作为一种强结构来发声。

注释

[1] 详见近期的结构设计教科书如：Allen，E. &Zalewski，W.. Form and Forces：Designing Efficient，Expressive Structures[M]. Wiley，2009；Muttoni，A.. The Art of Structures：Introduction to the Functioning of Structures in Architecture[M]. EPFL Press，2011；Saliklis，E.. Structures：A Geometric Approach[M]. Springer，2019.

[2] 对于卡尔曼作品的历史性介绍，详见：Maurer，B.. Karl Culmann und die graphische Statik[M]. GNT Verlag，1998.

[3] Kotnik, T.. Experiment as design method: On the possibility of the integration of the methodology of the natural sciences in architecture[M]// Moravansky,A., Kirchengast, A. (eds.). Experiments in Architecture.Jowis, 2011, 24-53.

[4] Kurrer, K.-E.. The History of the Theory of Structures:Searching for Equilibrium[M]. Ernst & Sohn, 2018.

[5] Abram，J.. Pier Luigi Nervi. Strength through Form，Form as Structure[M]//Pier Luigi Nervi.Architecture as Challenge. Milano：Silvana Editoriale，2010：41-57.

[6] Muttoni，A.. The Art of Structures： Introduction to the Functioning of Structures in Architecture[M].EPFL Press，2011：xii.

[7] 详见：Kilian，A. & Ochsendorf，J.. Particle-Spring Systems for Structural Form-Finding[J]. Journal of the International Association for Shell and Spatial Structures，2011，46 （148）：77-84； 或广泛使用的Rhinoceros插件，如Karamba3d或Kangaroo。

[8] K o t n i k, T., D’A c u n t o, P.. O p e r a t i v e Diagramatology: Structural Folding for Architectural Design[J]. Proceedings of the Design Modeling Symposium, Berlin, Springer, 2003, 193-203.

[9] Block, Ph., DeJong, M., Ochsendorf, J.. As Hangs the Flexible Line: Equilibrium of Masonry Arches[M].Nexus Network Journal, 2006, 8 (2): 13-24.

[10] Chilton, J.. The Engineer’s Contribution to Contemporary Architecture - Heinz Isler[M]. Thomas Telford, 2000.

[11] 利用图解静力学，卡尔曼分析出像费尔贝恩起重机（Fairbairn crane）这样的曲线结构中的应力模式与瑞士解剖学家冯·迈尔（von Myer）所记录的骨小梁内部形态（internal trabecular patterns）之间非常相似。1867年冯·迈尔绘制的股骨近端内部结构图，标志着揭示力学环境对骨小梁结构影响的严肃研究的开始。详见：von Myer G.H.. Die Architektur der spongiosa. Arch Anat Physiol Wiss Med[M]. 1867：34，615-628；Thompson D.W..On growth and form[M]. Dover，1992.

[12] Patrick Schumacher，principal of Zaha Hadid Architects，in Basulto，D.. Venice Biennale 2012：Arum / Zaha Hadid”[2012-8-31][EB/OL].[2020-09-11].ArchDaily.

[13] 关于探索与扎哈·哈迪德建筑师事务所后续作品中的关联性，可以对比： Schumacher，P.. The Congeniality of Architecture and Engineering：The future potential and relevance of shell structures in architecture[M]//Adriaenssens，S.，Block，Ph.，Veenendaal，D. & Williams，Ch. （eds.）. Shell Structures for Architecture：Form-Finding and Optimization. Routledge，2014.

[14] Fjeld，P.O.. Sverre Fehn：The Pattern of Thoughts[M].Monacelli Press，2009.