基于logistic分布密度函数的粒子群优化算法研究

王守亚，张 科

（淮南师范学院，安徽 淮南232038）

0 引言

粒子群算法［1-2］（Particle Swarm Optimization，PSO）是1995年Eberhart和Kennedy从生物种群的觅食行为中得到启发，提出的一种求解优化问题的智能算法.由于PSO算法具有实现简单、收敛速度快等优势，在许多求解优化问题的领域得到了广泛应用［3-6］.但随着对该算法求解精度和适用范围［7-10］的提高，该算法的早熟收敛和易陷入局部极值［11-12］等问题急需解决.孙俊等［13］人把PSO算法结合量子行为，提高了搜索性能；申翠香等［14］人提出了一种改进的粒子群算法，提高了全局搜索能力；封京梅等［15］利用惯性权重指数递减的粒子群优化算法求解最优值，减少了迭代次数，提高了精度；邱飞岳等［16］利用学习因子和混沌初始化策略提高了算法的精度等.

一些学者对PSO算法的研究提升了该算法的性能，但PSO算法在收敛速度和精度方面还有较大的提升空间.本文提出的一种基于logistic分布密度函数的粒子群优化算法，通过正态分布初始化策略和logistic分布密度函数改进权重值，和一些改进的PSO算法进行比较，本文提出的改进算法计算时间更短、精度更高.

1 基本的粒子群算法

设一个种群由n个粒子组成，搜索空间为D维，种群X=（X1，X2，…，Xn），其中，Xi=（xi1，xi2，…，xiD）T为D维向量，对应的速度Vi=（Vi1，Vi2，…，ViD）T，个体极值Pi=（Pi1，Pi2，…，PiD）T，种群极值Pg=（Pg1，Pg2，…，PgD）T，详细的参数说明可参考文献，每次迭代，粒子的速度和位置更新公式为：

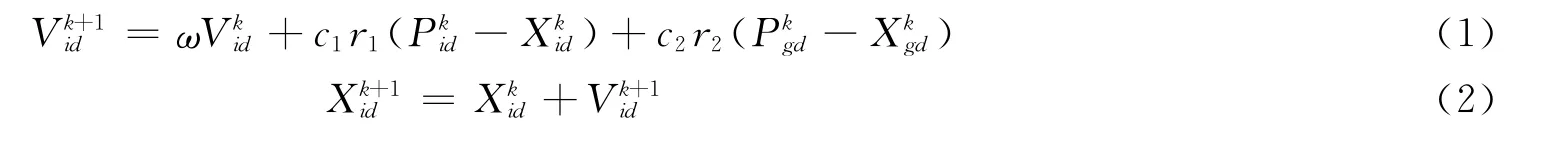
2 改进的粒子群优化算法

标准的粒子群算法的初始种群是随机生成的，种群的分布质量不佳，有待提高，可以把初始种群以正态分布的形式生成，提高初始种群质量.此外，改变惯性权重ω是相关研究人员改进粒子群算法的重点，ω的大小体现了PSO算法的全局和局部搜索能力，本文提出的基于logistic分布密度函数的PSO算法将ω按照logistic分布密度函数形式进行变化，并进行适当的修正.可以缩短搜索时间，提高搜索精度，降低算法陷于局部最优解的概率.

2.1 正态分布形式初始化种群

标准的PSO算法随机生成初始化种群，种群分布如图1所示，设种群数量N=30，种群质量不高，会增加迭代次数，降低求解精度等，本文采用正态分布的形式初始化种群，提高了种群的质量，种群分布如图2所示，设种群数量N=30，种群的分布服从公式（3）.

图1 随机分布的种群

图2 服从正态分布的种群

式中，u为期望，σ为方差.

2.2 基于logistic分布密度函数改进ω策略

与经典的线性递减权重法做比较，该权重ω的变化公式为：

式中，wmax和wmin分别为w的最大和最小值，t和tmax分别为当前和最大迭代步数.

线性递减权重法易理解、易实现，通过实验发现，在部分函数求最优解过程中表现不错，但对复杂问题求解方面还存在不足.主要是该方法的ω是在迭代过程中，由最大值以同样的速度不断减少到最小值，在搜索前期，全局搜索能力较强时间持续短，在搜索后期，局部搜索能力较强时间持续也短，算法容易陷入局部寻优中无法跳出.此外，ω固定的变化，也导致了该算法在求解非线性等复杂问题中存在不足.本文将ω的变化结合logistic分布密度函数进行改进，logistic分布密度函数表达式为：

式中：u是位置参数，σ是尺度参数，logistic分布属于位置-尺度参数族.

在本文中，取u=0，σ=10，并对logistic分布密度函数进行一定的修正，令ω的表达式为：

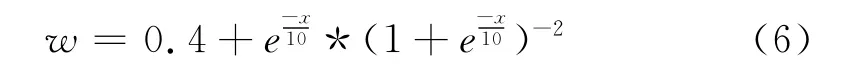
将公式（4）和（6）进行仿真，ω的曲线变化如图3所示.

从图3可以看出，改进后的权重值ω，在迭代的前期和后期分别能够保持一段时间的较大值和较小值，能够平衡PSO算法的全局和局部搜索能力，可以缩短搜索时间，提高搜索精度.

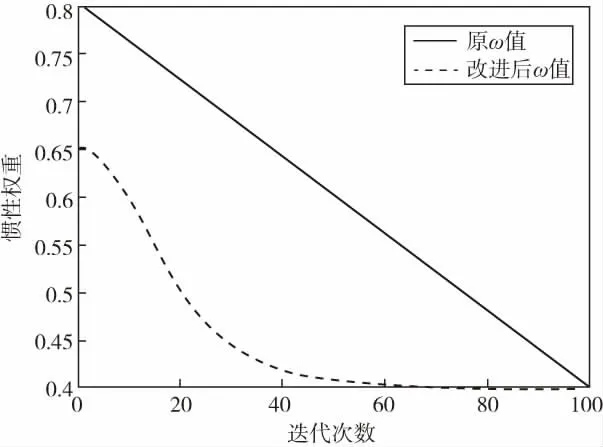
图3 改进前后ω的变化曲线

改进后的PSO算法实现过程如下：

①初始化粒子种群，使种群的分布服从正态分布；

②计算每个粒子的适应度值fit；

③初始化个体最优值pbest和全局最优值gbest；

④判断是否满足收敛条件，满足跳到⑦，否则执行⑤；

⑤根据公式（6）计算权重ω，根据公式（1）、（2）分别更新粒子的速度和位置，计算fit，更新pbest和gbest.

⑥若符合输出条件，算法结束，否则，返回继续执行；

⑦算法结束.

3 实验仿真及分析

本文提出的改进PSO算法与具有代表性的自适应权重法（记为：PSO-1）、随机权重法（记为：PSO-2）和线性递减权重法（记为：PSO-3）做比较，通过四个典型函数进行实验，对本文的基于logistic分布密度函数的粒子群优化算法（记为：PSO-4）性能进行详细分析.测试函数分别为典型的单峰值函数Sphere（记为：F1）、Step（记为：F2）和双峰值函数Griewank（记为：F3）、Rastrigin（记为：F4），四个函数的最优值均为0.

实验参数设置：种群数量设为50，搜索维度设为30，迭代次数设为100，加速度因子设为c1=1.5，c2=2.5，惯性权重设为ωmax=0.8，ωmin=0.4.电脑配置：型号为联想D5050，处理器为Intel（R）Pentium（R）CPUG3250＠3.20GHz，硬盘为500G，内存为4G.表1到表4分别为四种算法在不同测试函数上的运行结果，表中的平均值均是在运行20次后的结果.

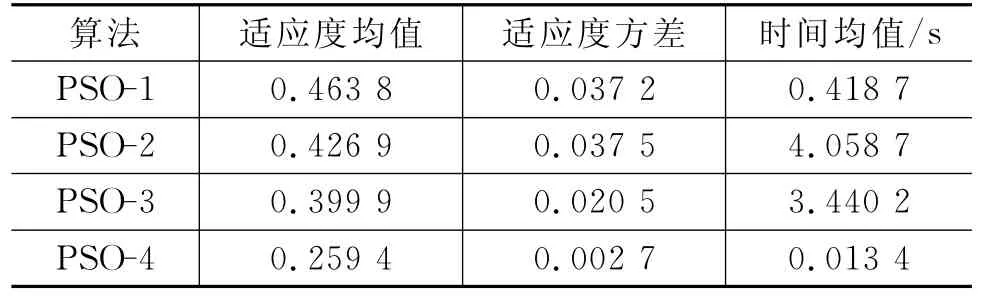
表1 算法在测试函数F1上运行结果

表4 算法在测试函数F4上运行结果

从表1可以看出，本文改进的算法PSO-4在测试函数F1上的适应度值是最接近最优值0的，而且方差是最小的，说明此算法寻优结果最稳定；从表2可以看出，PSO-4在测试函数F2上的适应度值比PSO-3略大，但方差是最小的，说明此算法寻优结果最稳定；从表3可以看出，PSO-4在测试函数F3上的适应度值比PSO-1略大，方差也略大，但适应度和方差数值均非常小，非常接近最优值0，能够满足实际应用；从表4可以看出，本文改进的算法PSO-4在测试函数F4上的适应度值为最优值0的，而且方差0，说明此算法寻优结果非常理想.从表1到表4可以看出，PSO-4平均运行时间最短，小于或远小于另外三种算法在典型测试函数上的运行时间.综上，可以看出，平均运行时间最短，搜索精度和稳定度高，性能整体优于其余三种算法.

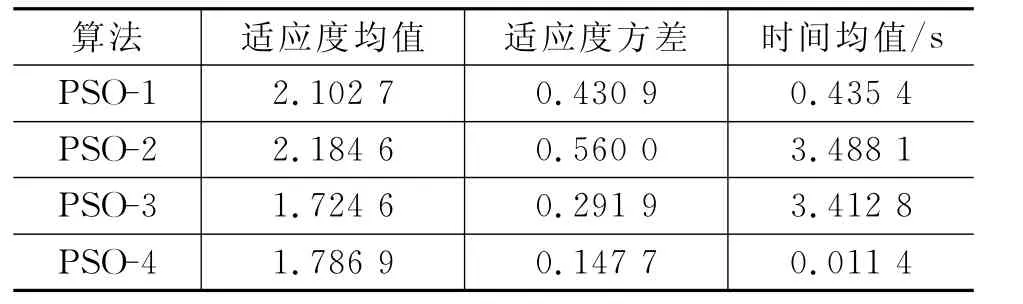
表2 算法在测试函数F2上运行结果

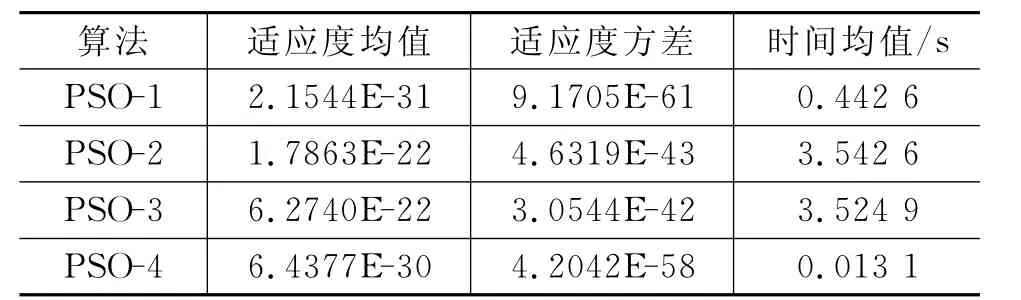
表3 算法在测试函数F3上运行结果

图4—图7是四种PSO算法在四种典型的测试函数上的迭代过程.

从图4可以看出，各种算法在在搜寻F1函数最优值过程中，都存在一定的“早熟现象”，算法PSO-4求解精度最高，最接近F1函数的最优值，收敛的速度略慢于PSO-1，但快于PSO-2和PSO-3.

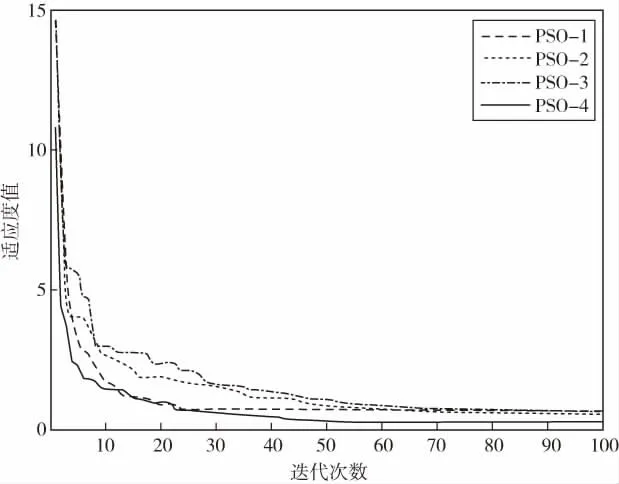
图4 Sphere函数迭代过程

从图5可以看出，各种算法在在搜寻F2函数最优值过程中，都存在一定的“早熟现象”，算法PSO-4求解精度最高，最接近F2函数的最优值，四种算法的收敛速度基本一样.

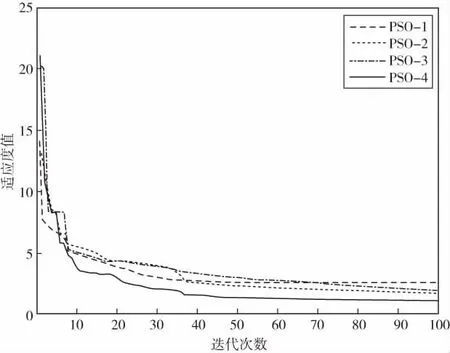
图5 Step函数迭代过程

从图6可以看出，PSO-1、PSO-2和PSO-3算法在搜寻F3函数最优值过程中，存在一定的“早熟现象”，PSO-4算法收敛速度最快，收敛精度最高.

图6 Griewank函数迭代过程

从图7可以看出，PSO-2和PSO-3算法在搜寻F4函数最优值过程中，存在一定的“早熟现象”，PSO-4算法收敛速度最快，收敛精度最高.

图7 Rastrigin函数迭代过程

总体上看，PSO-4算法相比另外三种算法，在四种典型的测试函数寻优过程中，都有较快的收敛速度和较高的精度值，在克服“早熟现象”方面，也优于或较优于另外三种算法.

4 结论

通过正态分布的形式初始化种群和利用修正的logistic分布密度函数改进权重值ω，提出本文的PSO-4算法，与另外三种算法在四种典型函数上进行测试，结果表明：PSO-4算法在收敛速度、精度和抵抗“早熟现象”等方面都有较显著的优势.在后期对该算法在实际应用等方面进行进一步的研究和优化.