一类多重循环群超可解性的判定
2021-07-08雒晓良
雒晓良
(太原师范学院 数学系,山西 晋中030619)
本文采用标准的术语和符号,例如按照文献[1,2].
设A=〈a1〉⊕〈a2〉⊕…⊕〈an〉是秩为n(n≥2)的自由Abel群,A的自同构群Aut(A)=GL (n,ℤ).对整数m,取α∈Aut(A)使得

取Λm(n)=A〈α〉,简记为Λm,它显然是一个二元生成的多重循环群.
定理1群Λm=A〈α〉是超可解群当且仅当m=±2且n=2.
证明 必要性.当m=2且n=2时,α(a1)=-a2,α(a2)=a1+2a2,即α(a1+a2)=a1+a2,此时
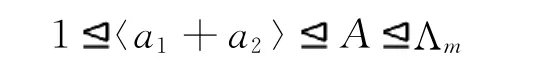
构成Λm的正规群列,并且因子群循环,从而Λm是超可解群.
当m=-2且n=2时,α(a1)=-a2,α(a2)=a1-2a2,即α(a1-a2)=-(a1-a2),此时
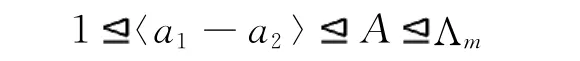
构成Λm的正规群列,并且因子群循环,从而Λm是超可解群.
充分性.若Λm是超可解群,则存在1≠N1Λm使得Λm在N1上的作用构成N1的幂自同构.
若N1∩A=1,则[N1,A]=1,即N1在A上作用平凡.∀1≠x∈N1,存在a∈A,i∈ℤ使得x=aαi,由x在A上作用平凡知αi在A上作用平凡,注意到α是A的自同构,从而αi=1即x=a∈A,矛盾,因此N1∩A≠1.
取1≠a∈N1∩A,有α在〈a〉上的作用构成〈a〉上的幂自同构,但a是无挠的,故α()a=±a.设a=x1a1+x2a2+…+xnan,则
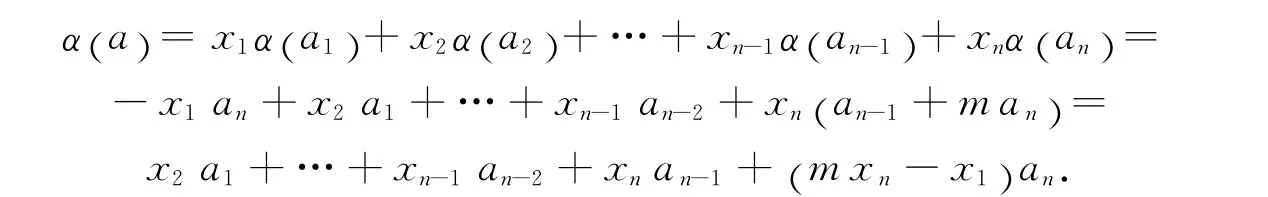
1.若α(a)=a,则x1=x2=…=xn且xn=mxn-x1,即(m-2 )xn=0,由a≠0知m=2.
此时a=x1(a1+a2+…+an),故可取N1=〈a1+a2+…+an〉,有N1Λm.下面在Λm/N1中考虑.因为〈α〉N1/N1≅〈α〉,故将α在Λm/N1上的作用仍用α来表示,即Λm/N1=A/N1〈α〉.显然有A/N1=〈a1〉⊕〈a2〉⊕…⊕〈an-1〉≅〈a1〉⊕〈a2〉⊕…⊕〈an-1〉.若n>2,则有
这个蜘蛛精……是人?青辰一边听着天葬师的话,一边仔细打量。那唐飞霄矮小瘦弱,整个身子都裹在硬甲中,只有一颗硕大的光头露在外面,看起来怪诞而不合比例。自己先入为主,竟将其当做了蜘蛛精,着实闹了个笑话。
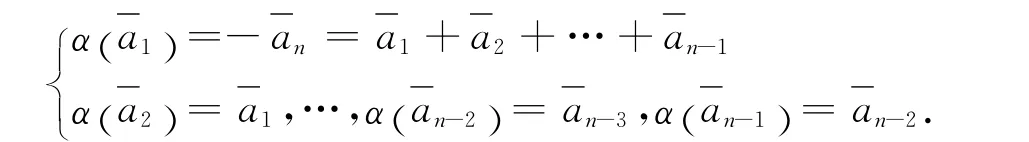
因Λm/N1是超可解的,则存在1≠N2/N1Λm/N1使得Λm/N1在N2/N1上的作用构成N2/N1的幂自同构.同样讨论可得N2/N1∩A/N1≠1.取有α在上的作用构成上的幂自同构,但是无挠的,故则
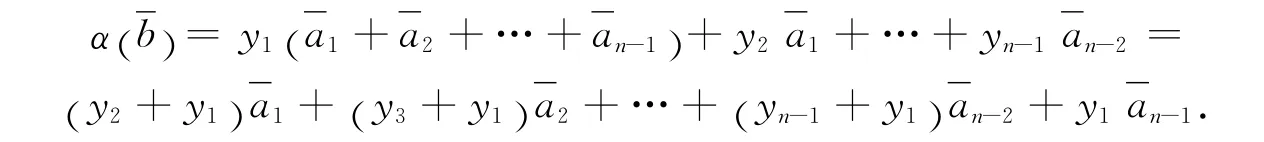
2.若α(a)=-a,则xi=-xi+1(1≤i≤n-1)且(m+1 )xn=x1,需对n的奇偶性分别讨论.
1)当n为奇数时,mx1=0即m=0.此时a=x1(a1-a2+a3-a4+…+an),故可取N1=〈a1-a2+a3-a4+…+an〉,有N1Λm.下面在Λm/N1中考虑,将α在Λm/N1上的作用仍用α来表示,即Λm/N1=A/N1〈α〉.显然有
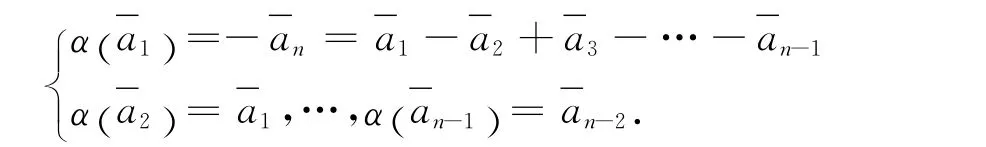
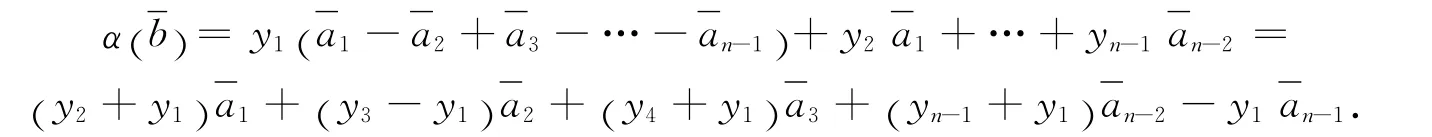
2)当n为偶数时,(m+2 )x1=0即m=-2.此时a=x1(a1-a2+a3-a4+…-an),故可取N1=〈a1-a2+a3-a4+…-an〉,有N1Λm.下面在Λm/N1中考虑.将α在Λm/N1上的作用仍用α来表示,即Λm/N1=A/N1〈α〉.显然有若n>2,
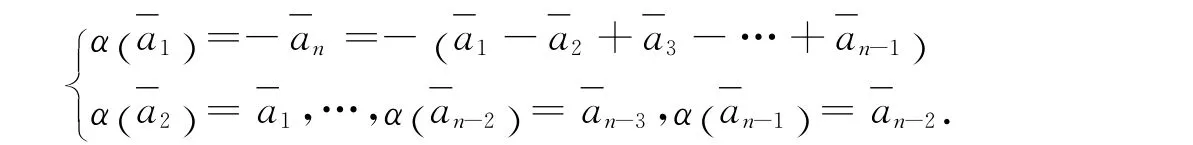
因Λm/N1是超可解的,则存在1≠N2/N1Λm/N1使得Λm/N1在N2/N1上的作用构成N2/N1的幂自同构.同样讨论可得N2/N1∩A/N1≠1.取上的作用构成上的幂自同构,但b是无挠的,故则
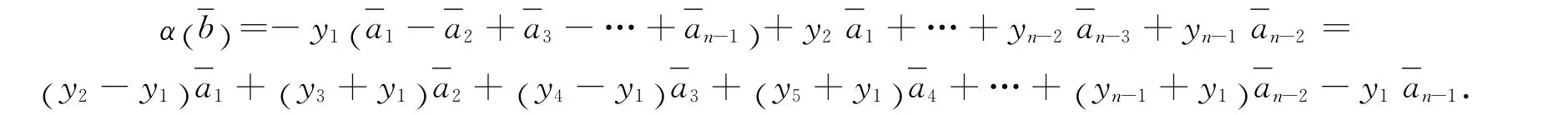
进一步计算可得,
1)当m=2,n=2时,
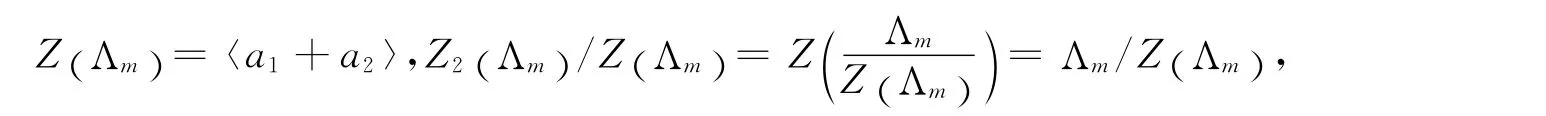
即Z2(Λm)=Λm,从而Λm构成幂零群.
2)当m=-2,n=2时,A∩Z(Λm)=1,即此时Λm不是幂零群.
