纤维掺量对玻璃纤维增强水泥板弯曲性能的影响

卢 娟，张亚芳，程从密，霍永杰

广州大学土木工程学院，广东广州 510006

水泥是基建工程中应用最为广泛的胶凝材料，具有耐久性好和抗压强度高等优点，也存在抗拉强度低、抗裂性差和延伸率较低等不足，在一定程度上限制了应用. 因此，研究者把纤维掺到水泥中，利用纤维来改善水泥的性能[1-2].

在纤维增强水泥材料中，玻璃纤维是常见的水泥基材料的增强物质[3-4]，具有较低的比重和吸水率、较高的弹性模量、抗拉强度和质量[5-7]. 很多学者对玻璃纤维增强水泥(glass fiber reinforced cement， GRC)的性能进行了研究[8-11]. GRC被广泛应用于包覆板[12]、电信塔[13]和永久模板工程[14]等领域中. 其中，不少构件用来承受弯曲作用，但目前缺乏相应的对其进行较为完整有效理论分析的模型. GRC的抗弯性能可通过四点弯曲试验进行研究[15-16]，且性能受纤维方向分布的影响较大[17-19]. 目前，有关GRC数值模拟的研究多是考虑处于随机分布状态的纤维，而涉及纤维取向/定向玻璃纤维对GRC力学性能影响的分析尚少有研究. 本研究通过物理试验与数值模拟分析相结合的方法，在四点弯曲加载下，分析定向玻璃纤维的阻裂机理以及不同纤维掺量对GRC板力学性能的影响，建立了基于有限元分析并适用于玻璃纤维增强水泥的数值模型，并通过细-宏观多尺度结合的方法，研究了玻璃纤维对水泥板的增强增韧机理，为定向玻璃纤维增强水泥材料的加固提供了一种有效的分析方法.

1 物理试验

1.1 材料及配比

1.1.1 材 料

试验中使用的GRC由以下部分组成：低碱度硫铝酸盐水泥、标准砂、水、高效减水剂和玻璃纤维. 其中，玻璃纤维单股线密度为98 tex.

1.1.2 材料配合比

水泥砂浆基体材料的配比为m(水泥)∶m(标准砂)∶m(水)∶m(减水剂)=1∶1∶0.36∶0.01. 将不同体积分数的玻璃纤维制备入水泥砂浆，得到不同掺量的GRC试件. 纤维的体积分数分别为0、0.5%、1.0%、1.5%和2.0%，对应的试件编号分别为GRC-0、GRC-1、GRC-2、GRC-3和GRC-4. 为研究与加载方向平行的玻璃纤维对材料性能的影响，设计1组纤维体积分数为0.7%的试件，编号为GRC-5. 其中，0.5%的纤维垂直于加载方向(纵向纤维)，0.2%的纤维平行于加载方向(横向纤维).

1.1.3 玻璃纤维束的准备

图1为GRC试件的模型图，其中，F为加载力，纵向纤维与加载方向垂直. 图2为试件GRC-3与GRC-5中的纤维束分布. 本实验使用330 mm×13 mm×50 mm的砂浆板模具，用小木棍将长度为320 mm的玻璃纤维束进行黏接固定，如图2(a). 图2(b)为试件GRC-5的玻璃纤维束分布.

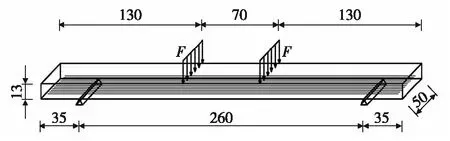
图1 GRC试件的模型图(单位：mm)Fig.1 Schematic diagram of fiber orientation of GRC specimen(unit：mm)

图2 GRC-3与GRC-5的纤维束分布Fig.2 (Color online) Fiber bundles of GRC-3 and GRC-5

1.2 试件的制备和养护

使用普通的砂浆搅拌机进行搅拌，旋转速度为80 r/min，并将试件分层浇筑. 第1层浇筑后放入纤维束，继续浇筑第2层. 每层浇筑后都用振动台压实，以去除空气间隙，最后将周围的多余浆体擦拭干净. 静待1 h后，用保鲜膜密封，将试件转移到相对湿度大于95%的地方静置. 24 h后脱模，将试件放入水中养护26 d，进行抗弯强度测试.

1.3 试验方法及测试内容

图3为GRC的抗弯强度试验. 本试验依据GB/T 15231—2008[20]标准进行，采用广州大学土木工程实验室的WHY-50微型控制全自动压力试验机，加载速度为0.5 mm/min，采集数据包括荷载和位移.

图3 GRC的抗弯强度试验Fig.3 (Color online) Bending test of GRC

2 试验结果与讨论

2.1 弯曲破坏形式

图4为试件GRC-0和GRC-5的断裂图. 在四点弯曲加载时，试件断裂均发生在中间纯弯段.由图4可知，试件GRC-0未掺入玻璃纤维，表现出明显的脆断特性. 当试件出现裂缝后，裂缝迅速向上扩展直至断裂. 而掺加了玻璃纤维的GRC-5，在加载过程中会听到纤维被拉断的声音. 底部出现裂缝后，裂缝向上扩展较为缓慢，发展路径相对曲折，同时，试件产生较大变形. 当裂缝逐渐扩展到试件上边缘时，试件仍可以承受一定的荷载，没有发生脆断现象，破坏形态表现为“裂而不断”.

图4 不同玻璃纤维掺量试件的断裂图Fig.4 (Color online) Bending diagram of different glass fiber additives

试件的玻璃纤维掺量越多，当微裂纹萌生后，随着加载持续，裂缝向上扩展的时间越长，呈现的延性破坏特征越为明显.

2.2 纤维掺量对荷载-位移曲线的影响

图5(a)为试件GRC-0至GRC-4的荷载-位移曲线. 对于未添加纤维的试件GRC-0，当拉应变达到极值时，试件底部首先出现裂缝，随后裂缝迅速扩展到上面，试件断裂. 荷载-位移曲线表现为荷载陡降到0. 而对于添加纤维的试件(GRC-1至GRC-4)，峰值荷载随着纤维掺量的增多而不断增大，说明纤维对水泥的增强作用在不断提高，同时荷载-位移曲线AB段(此时处于纤维断裂时期)的包络面积也随之增大，说明试件的韧性也随玻璃纤维掺量的增加而增大. 图5(b)与图5(c)分别为试件GRC-0与试件GRC-4的破坏断面图. 从图5(b)和图5(c)可见，试件GRC-0的断口较为平整，而试件GRC-4断口处有因拔出而突出的纤维. 这是因为在试件裂缝扩展过程中，纤维会跨过裂缝的两侧发生桥连现象. 由于纤维具有较高的弹性模量，所以未被拔出或拉断的纤维对微裂缝仍有一定的限制作用，可传递并承担其中的一部分拉力，使荷载-位移曲线与坐标轴的包络面积更大，文献[21]的研究也有相同的结果.

图5 GRC-0至GRC-4荷载-位移曲线与破坏断面图Fig.5 (Color online) Load-displacement curve and sectional drawing of GRC-0 to GRC-4

图6为试件GRC-1与GRC-5的荷载-位移曲线与破坏断面图.由图6可见，试件GRC-5与GRC-1的主要差别在于纤维呈网格状(即GRC-5存在横向纤维)，但二者荷载峰值结果相差不大，说明横向纤维对荷载峰值影响不大. 从图6(c)可见，横向纤维限制了受力纤维的滑移，因此试件GRC-5断裂后纤维更短，即为纤维断裂. 而图6(b)试件断裂后纤维较长，即为纤维拔出.

图6 GRC-1与GRC-5荷载-位移曲线与破坏断面图Fig.6 (Color online) Load-displacement curve and sectional drawing of GRC-1 and GRC-5

3 数值模型建立

本研究使用RFPA3D软件进行数值模拟.图7为GRC数值模型，基体尺寸为330 mm×13 mm×50 mm. 对整体试件进行计算单元划分，均为边长1 mm的正六面体单元，总单元个数为27万. 加载方式为位移加载，加载步长为0.01 mm/步，共加载400步.

图7 GRC数值模型(单位：mm)Fig.7 (Color online) GRC numerical model(unit：mm)

RFPA3D软件采用Weibull双函数曲线[22]对各相材料细观单元的强度、泊松比、弹性模量和密度等物理量进行非均匀性赋值，即

(1)

其中，φ(x)为材料具有某一力学性质的细观微元体的概率密度；x为材料细观单元的力学性质(弹性模量、抗压强度、泊松比和密度)；x0为单元参数所对应的平均值；m为材料的均质度系数，m越大，表明材料分布越均匀.

表1为根据试验测得的三维数值计算模型中各组分的材料力学参数赋值.

表1 数值模型各组分材料力学参数1)Table 1 Parameters of varied materials

σ1≥σt

(2)

其中，σ1为最大主应力；σt为材料的极限拉应力.

当单元满足摩尔库伦准则时，该单元发生剪切损伤，即

(3)

其中，φ为单元的摩擦角；σ3为最小主应力；σc为材料的极限抗压强度值. 最大拉应力准则具有优先权.

4 数值模拟结果

4.1 纤维掺量对荷载-位移曲线的影响

图8为试件的荷载-位移曲线. 由图8(a)可见，随着纤维掺量的增加，试件的峰值荷载逐渐提高.在弹性阶段(oA段)，各试件曲线几乎完全重合，表明纤维掺量对试件抗弯性能弹性阶段的影响甚微；进入非弹性阶段(AB段)后，纤维掺量越大，试件的抗弯能力越强，峰值荷载越大；试件达到峰值荷载B点后，随荷载继续增大，试件开始出现损伤，承载力下降；B点以后，荷载主要由纤维来承担；当过C点后，与GRC-0相比，添加纤维试件的CD段出现荷载增大的现象，因为此时纤维虽然发生损伤，但未完全损坏，纤维可承受一定的荷载，并且纤维掺量越多，试件韧性越强，可承受荷载能力越强.

图8 试件荷载-位移曲线Fig.8 Load-displacement curve of specimen

图8(b)对比了试件GRC-1与GRC-5的荷载位移曲线. 由图8(b)可见，GRC-1与GRC-5荷载-位移曲线发展趋势一致，荷载峰值相近，横向纤维对试件的承载力作用不大，对韧性影响甚微，与物理试验结果一致.

表2为各试件的物理试验与数值模拟峰值荷载结果. 由表2可见，数值模拟分析中GRC-4的峰值荷载f2最高达到510.49 N，物理试验中的峰值荷载f1最高达到515.43 N，数值模拟与物理试验结果较吻合. 二者之差的绝对值|Δf|=|f1-f2|最大仅为13.10 N. GRC-4对GRC-0的相对韧度值最高可达5.56，表明掺加玻璃纤维对试件的韧性具有显著提高作用.

表2 各试件物理试验与数值模拟峰值荷载结果Table 2 Peak load results of numerical simulation and physical tests

断裂能Gf为描述混凝土断裂性能的参数，即单位面积断裂时所需消耗的能量[24]，计算公式为

Gf=(W0+W1+W2)/A

(4)

其中，W0为荷载-位移曲线从开始加载直至拟合点时的包络面积；W1为两支座间试件的重力所做的功， 因此可忽略不计， 有W1≈0；W2为拟合点前重力的附加功，W2=mgδmax，m为试件支座间的质量， g为重力加速度，δmax为跨中最大挠度；A为断面的面积，A=t(h-a0)，t为试件宽度，h为试件高度，a0为初始裂缝高度，此处忽略不计.

表3为GRC板的物理试验和数值模拟断裂能及对比. 由表3可见，GRC板断裂能随玻璃纤维掺量的增大而显著提高. 当玻璃纤维体积分数为2.0%时，物理试验所得断裂能Gf1是素水泥试件的5.6倍，数值模拟结果得到的断裂能Gf 2是素水泥试件的5倍. CHENG等[25-26]分析了随机分布玻璃纤维对水泥断裂能的影响，实验结果表明，GRC的断裂能随着纤维掺量的增加而显著增大，这与本研究的研究结果一致.

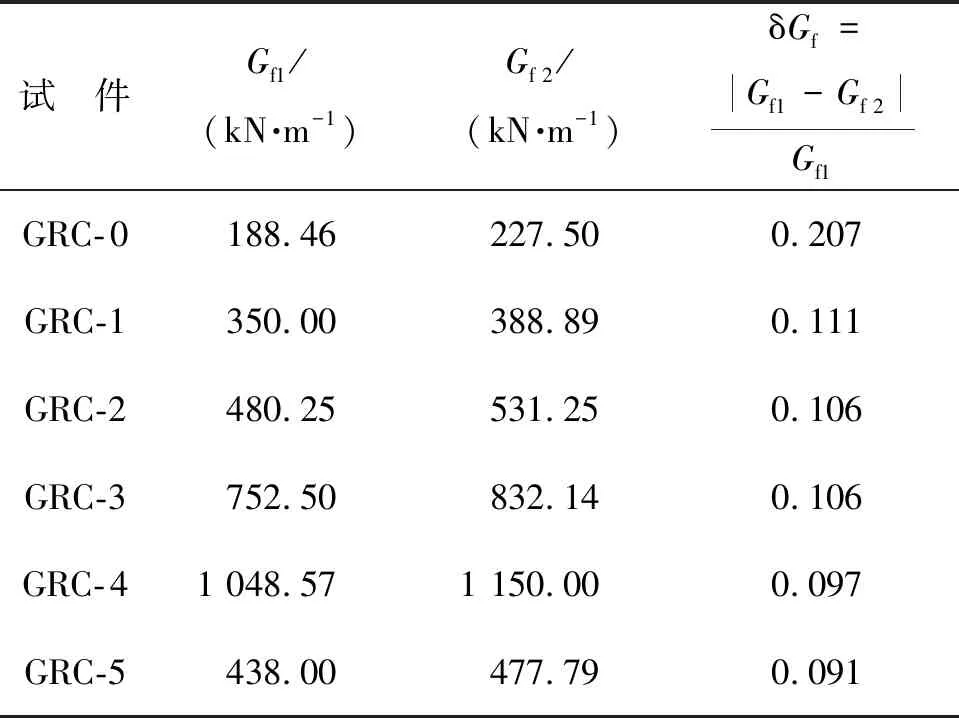
表3 物理试验与数值模拟断裂能及其对比值Table 3 Comparison of fracture energy between physical test and numerical simulation

5 结 论

采用物理试验和数值模拟方法，研究了不同掺量的定向玻璃纤维增强水泥板的四点弯曲断裂力学行为，可知：

1)纤维体积分数在0.5%～2.0%时，试件峰值荷载随着定向纤维掺量的增多而增大. 在物理试验中，纤维体积分数为2.0%试件的峰值荷载为515.43 N，数值模拟的峰值荷载为510.49 N. 添加横向纤维对承载力的提高影响甚微.

2)所有试件均在纯弯段断裂. 素水泥板试件的荷载-位移曲线在峰值荷载后的劣化阶段急剧下降.添加纤维试件的在试件底部出现裂缝后，发生损伤但未完全损坏，仍具有一定承载力，荷载-位移曲线在峰值荷载后的劣化阶段呈现出延性破坏特征. 纤维掺量越大，裂缝扩展模式愈加曲折，承载能力越强. 数值模拟分析与物理试验结果吻合.

3)通过断裂能分析，纤维体积分数在0.5%～2.0%时，纤维掺量越多，受荷载作用发生破坏时做的功越多，韧性越好. 当玻璃纤维体积分数为2.0%时，实验所得断裂能是素水泥板试件的5.6倍，数值模拟分析得到的断裂能是素水泥板试件的5倍，结果较为一致.