用改进的落体法测量重力加速度
2021-07-07林彦嘉
林彦嘉,林 鹏
(1.西南大学物理科学与技术学院,重庆 400715,2.西北核技术研究所,陕西 西安 710024)
在经典物理学中,重力加速度是一个重要的物理学常数。地球上不同的纬度、海拔高度以及不同的地质条件,都对重力加速度的值有影响。在大地测量学中,重力加速度数据可以用来确定大地水准面,在制图学中,可以用来计算高程。对重力加速度值的精确测量,在计量科学、天文学、资源勘探和惯性导航等领域都有非常重要的作用[1]。
测量重力加速度在物理学中是一个基本的实验。重力加速度的测量方法较多,主要有物理摆法[2,3]、自由落体法[4]、倾斜气垫导轨法[5]和平衡法[6]等。还有其他新方法,比如刘艳峰利用CCD结合杨氏模量测量仪给出了重力加速度测量方法[7],张鹏娟提出了利用液体黏滞系数测定仪来设计测量当地的重力加速度的方法[8],李应法利用弦振动方法来测量重力加速度[9]。对应这些传统的方法,前人研制了相应的重力加速度测量仪。对于常用的自由落体法,为了克服电磁铁剩磁对下落小球初速度的影响,往往采用两组光电门,在两次下落实验中改变光电门之间的距离,通过测定两次实验中小球通过两光电门的时间来求得重力加速度。也有在自由落体法中采用三组光电门[10],以第一组光电门为时间和距离的起点,测量小球经过第二组和第三组光电门的时间来求重力加速度。本文设计了一种改进的自由落体法测量重力加速度测量装置,该装置只采用一组光电门,并将下落小球改为竖直下落的传信杆。与传统使用的自由落体法装置相比,本文设计的装置使用起来更加简便、快捷,并具有较高测量精度。
1 实验原理及方法
1.1 测量原理
常用的自由落体测重力加速度方法,采用的是二次测量法。如图1所示,小球从位置“O”做初速度为0的落体运动,经过第一个光电门位置“A”时,初速度为v0,以此位置作为下落时间和距离起点。小球经过时间t1,自由落体到第二个光电门“B”,下落距离为s1;将第二个光电门移动到位置“C”,小球再次从位置“O”做初速度为0的落体运动,到达位置“C”的时间为t2,下落距离为s2。小球运动满足如下方程。

图1 自由落体法测量原理图
(1)
(2)
由此可得重力加速度为
(3)
测量两次实验中小球的下落时间,带入(3)即可求得重力加速度。如果装置有3个光电门,则小球一次下落可测得两个时间,完成重力加速度的测量。小球的横截面是圆形的,实验中小球的不同部位经过光电门时,会造成测量时间偏差。二次测量法中,由于剩磁的影响,初速度v0可能会不同,给实验带来较大误差。
1.2 改进方法
为简化实验过程,将实验装置进行改进。下落的小球改为竖直下落的传信杆。为减少光电门的数量,只用一组光电门,而将杆下落的距离精确刻度在传信杆上,即在杆的末端加工环形的缺口和凸台,光电门位置偏离杆中心。当杆竖直下落,缺口对着光电门时,光电门是通光状态,当杆的凸台对着光电门时,是遮光状态。如图2所示,A是第一个缺口开始位置,B是第二个缺口开始位置,C是第三个缺口开始位置。AB之间的距离为s1,AC之间的距离为s2。传信杆直径为6 mm,末端凸台部分直径为9.6 mm。限位框的内径为6.1 mm,略大于杆的直径。光电门中的发光管和光敏管的外径皆为2 mm,两管分别置于绝缘套中,定位在对应的传信杆末端两侧位置。两绝缘套对应端的端口直径皆为0.3 mm,限制光束出射孔和光束入射孔的面积大小。光电门电路如图3所示,直流电源电压为9~12 V,电阻R1的阻值为1 kΩ,电阻R2的阻值为20 kΩ。光电门的信号由电阻R2输出,通光时输出直流电压信号,遮光时电压信号为0。
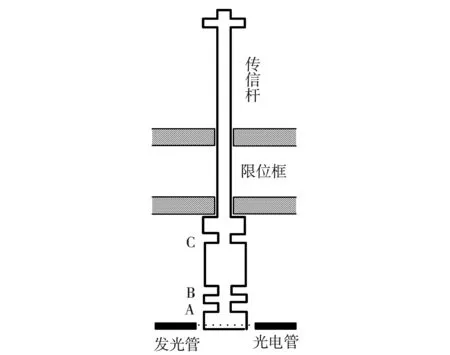
图2 测量装置示意图

图3 光电门电路
如图4所示,整个重力加速度测量系统由直流电源、g测量装置和数字示波器组成。当传信杆下落时,缺口经过光电门时输出相应的直流方波电压信号,信号由示波器记录。在示波器上通过判读第一个方波到第二个方波的时间间隔得到t1,判读第一个方波到第三个方波的间隔得到时间t2。带入公式(3)即求得重力加速度g。

图4 测量系统组成
1.3 不确定度分析
实验误差主要来源于下落距离(s1和s2)和时间间隔(t1和t2)测量的不准确。重力加速度是一个间接测量物理量,根据不确定度传递规律,由公式(1)-(3)可得重力加速度g的测量相对不确定度η计算公式
(4)
式中,Δt和Δs分别为时间(t1和t2)和距离(s1和s2)的测量不确定度。Δs由精密机械加工控制,取最大值0.01 mm。Δt受空气阻力和摩擦力影响,低速运动时空气阻力可忽略,当传信杆与限位框架不接触或充分润滑时,摩擦力影响也可忽略。综合起来,Δt取0.02 ms,主要来源于示波器判读误差。
首先,固定s2的大小为24 mm,取重力加速度的理论值g=9.80 m·s-2,然后根据公式(4)来确定s1的取值。假定位置A离初始自由落体位置为3 mm,6 mm和9 mm,可得到不同的初始速度v01,v02和v03。三者中v01最小,v03最大。然后改变s1的值,计算不同初速度时重力加速度的相对不确定度η随s1的变化关系。计算结果如图5(1)所示,相对不确定度随v0的增大而增大。在s2确定的情况下,s1为s2的五分之一到三分之一范围内时,相对不确定度最小。所以,在本设计中,取s1为6 mm。当位置A离初始自由落体位置为3 mm时,理论设计的重力加速度的相对测量不确定度为0.49%。进一步计算表明,s2的值对重力加速度的相对不确定度η也有影响,如图5(2)所示,s2增大,η变小。

(1) v0不同
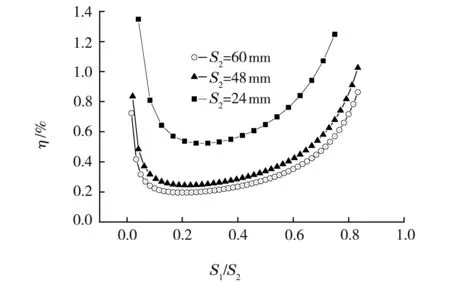
(2) s2 不同图5 相对不确定度随s1位置的变化
2 实验测量
开启直流电源给光电门供电,直流电压9~12 V;调整数字示波器采样率到200 MSa/s,选择示波器存储深度为14 M,触发位于测量时长的50%处,设置示波器触发方式为单次触发且触发电平为1 V;调整测量装置为竖直状态,将传信杆提升到高位;数字示波器处于待触发状态,然后释放传信杆。当第一个缺口经过光电门时,系统触发,输出测量波形如图 6所示。第一个方波对应位置A,第二个对应位置B,第三个对应位置C,第四个是传信杆反弹后位置C对应的输出。

(1)判读t1
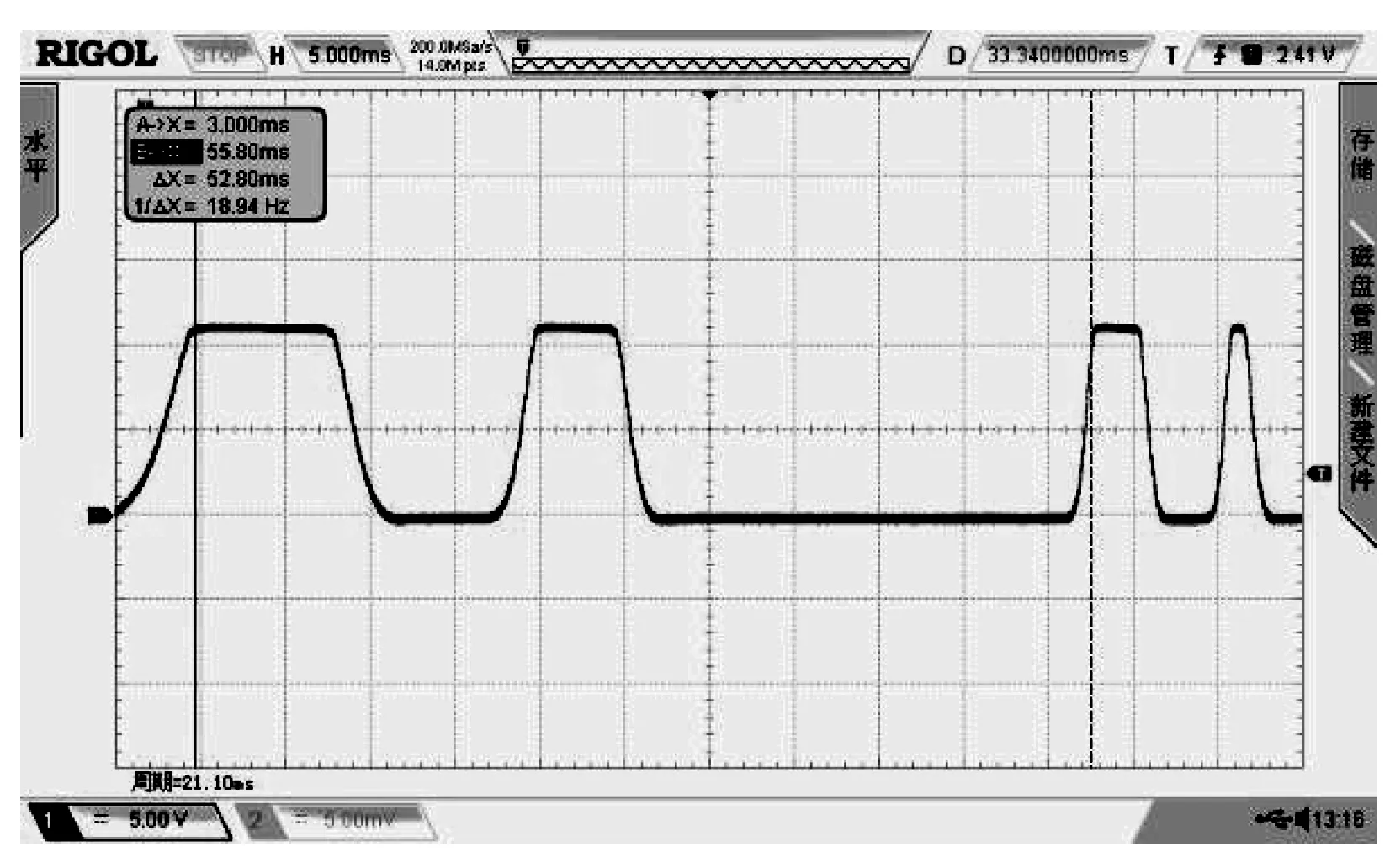
(2) 判读t2图6 实验测量时间判读波形
将示波器的光标打开,由第一和二个方波判读时间t1,第一和第三个方波判读时间t2。判读时既可取方波的前沿,也可取后沿。前面计算表明,初速度对相对不确定度有影响,取前沿时初速度小于取后沿时的初速度,因此取前沿优于取后沿。多次实验,实验结果例于表1中。

表1 实验结果
对表1中的重力加速度测量值及其不确定度进行统计,得到重力加速度g的值为
g=9.77±0.04 m·s-2
重庆地区的重力加速度的公认值为9.79 m·s-2,测量值比公认值小0.2%,说明测量结果是可信的,本装置的测量精度较高。
3 结 语
设计了一种应用单光电门的自由落体重力加速度测量方法,对初速度v0和下落距离s1、s2等因素对重力加速度测量相对不确定度的影响进行了计算分析,利用新设计方法对重力加速度进行了实验测量,得出如下结论:
(1)s2固定条件下,初速度越大,g的相对不确定度也越大,因此,实验中光电门和初始下落位置要尽可能靠近;
(2)v0固定条件下,s2越大,g的相对不确定度越小,在实验装置的有限空间内,应选择s2尽量大一些;
(3)s2固定条件下,s1为s2的五分之一至三分之一范围内时,g的相对不确定度较小;
(4)本改进方法设计的测量装置,对g的测量相对不确定度可达0.5%,实验测量结果与标准值偏差为0.2%,这说明本方法是可行的,且具有较高测量精度。
