基于决策树的航空器离港滑出时间预测方法和模型
2021-07-07唐小卫林有超任思豫
陈 祯 唐小卫* 林有超 任思豫
(南京航空航天大学民航学院1) 南京 211106) (中航空管系统装备有限公司2) 上海 200241)
0 引 言
当前我国大型繁忙机场采用的协同决策(collaborative decision making,CDM)系统通过集成空管、航空公司、机场三个独立的子系统搭建出一个信息交互、数据共享的航空运输一体化平台,实践表明:CDM系统在减少航班总体延误、扩大机场容量等方面起到了积极作用.对于每一个离港航班,目前CDM系统是用每个航班在跑道上的计算起飞时刻减去平均滑行时间得到其在机位上的推出时刻,但航班离港滑行的过程具有较大的不确定性,仅凭经验预测滑行时间的传统管理模式已不能满足CDM系统的要求.因此,研究影响离港滑行时间的关键因素并设计合适的算法来提高离港滑行时间预测的准确性对优化离场顺序、提高CDM机制下起飞时刻的执行率具有重要意义[1].
国内外对航空器离港滑行时间预测的研究主要涵盖特征选取和模型方法两个方面.在特征选取方面,Kistler等[2-3]考虑了滑行距离、进离港交通量、跑滑结构等影响滑行时间的因素,一定程度上丰富了特征变量集;Jordan等[4]进一步引入航空公司、滑行方向等虚拟变量并构建交互特征,有效提升了模型的预测精度;Ravizza等[5-6]利用欧洲机场滑行道的专有特点构建滑行转弯角度与距离特征,在欧洲机场的样本集上取得了良好的预测结果;冯霞等[7]将滑出时间预测分为两个阶段,先利用已知特征预测滑出期间使用同跑道起降的航班数量,再将其作为输入变量构建滑行时间预测模型,发现该方法的预测效果优于直接预测;刘继新等[8]对航空器滑出时间的影响因素进行分析,验证了场面流量的影响最为显著.在模型方法方面,Balakrishna等[9]在随机动态规划的概率框架中采用强化学习的方法进行滑行时间预测;Zhang等[10]建立计量经济学回归模型预测无阻滑行时间,在计算排队长度时考虑了飞机超越等因素,同时将跑道构型、地面延误程序和天气作为解释变量,使得模型可以广泛应用于欧美机场滑行延误对比;Herrema等[11]研究了机器学习在滑行时间预测上的运用,将神经网络、回归树分析、强化学习和多层感知方法四种机器学习方法运用于戴高乐机场实际运行数据,得出回归树模型预测效果最好.
以上研究主要聚焦于每个特征单独对滑行时间的影响以及特征构建后的模型选择,少有研究考虑特征间相互作用会对滑行时间预测产生的效果.因此,文中基于滑出时间的影响因素构建一次特征变量,运用特征工程构建交互特征,与一次特征共同构成初始变量集.考虑到初始变量集可能存在冗余特征对预测产生一定的影响,因此基于决策树算法从所构建的大量特征中筛选出一部分最重要的特征作为最优特征变量集构建离港滑行时间模型,并将该模型与仅使用一次特征构建的模型对比验证.
1 滑出模型的特征构建
数据来源于首都机场2019年10月—2020年1月的航班运行数据,考虑到36R跑道为首都机场主离港跑道,因此选取36R跑道的航班运行数据进行研究分析.
1.1 一次特征构建
1) 滑行距离 一般而言离港滑行时间随着滑行距离的增加而增加,因此首先考虑建立离港滑行时间和滑行距离的一元线性回归模型.现有数据无法获得每个航班的具体离港滑行路径,通过机场地面管制部门提供的场面运行规则,依据机场CAD底图量取各机位至跑道口的滑行距离,将数据进行归一化处理后得到
Tout=0.081D+0.184
(1)
式中:Tout为离港滑行时间,min;D为离港滑行距离,km;表1中的各项评价指标分别为该预测模型的±3 min准确度、±5 min准确度、拟合优度和相关系数,可见滑行距离与离港滑行时间的相关性很低,滑行时间不会受到滑行距离的显著影响.

表1 评价指标
2) 拥堵变量 航空器的离港滑行会占用跑道、滑行道等场面资源,航空器间由于资源占用而发生冲突,当冲突发生时航空器需在原地等待直至冲突解除.场面拥堵加剧导致冲突发生的频率变高、解除冲突的时间变长,进而滑行时间增加.因此构建了两个拥堵变量,即某个航班滑出期间内使用同跑道离港的航班数量(Ntxot)和进离港瞬时流量(Nins).Ntxot指在航班撤轮挡推出时刻至计算起飞时刻的这段时间内使用同跑道离港的航班数量;Nins指在航班撤轮挡推出时刻的场面进离港瞬时流量.
图1分别给出了Ntxot,Nins与Tout的相关性分析,相关系数分别为0.88和0.47,可见Ntxot,Nins与Tout具有较强的相关性,但在流量相同的情况下,出港滑行时间相差可达30~40 min,说明除了上述2个拥堵变量,还存在其他影响离港滑行时间的因素.

图1 Ntxot,Nins与Tout的相关性分析
3) 推出前15 min离港航班平均滑行时间tdep通过挖掘相邻时间段内使用同跑道离港的航空器的滑行时间之间的关系,以15 min为一个单位将滑行时间离散化处理,发现推出前15 min使用同跑道起飞的其他航班的平均滑行时间tdep与该航班的滑行时间具有一定的相关性.图2为tdep与Tout的相关性分析,结果显示相关系数为0.47.
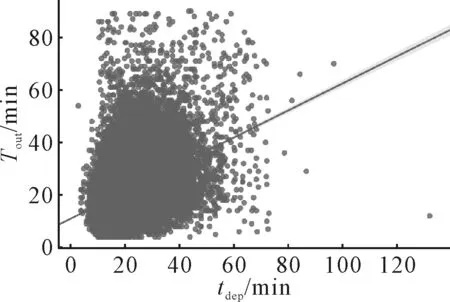
图2 tdep与Tout的相关性分析
4) 机型类别 不同机型的操纵性能不同,其本身滑行时的速度也有差异.航班样本涉及C、D、E、F四种机型,在相同范围的滑行距离下,各类机型的样本数量、平均滑行时间、标准差见表2.
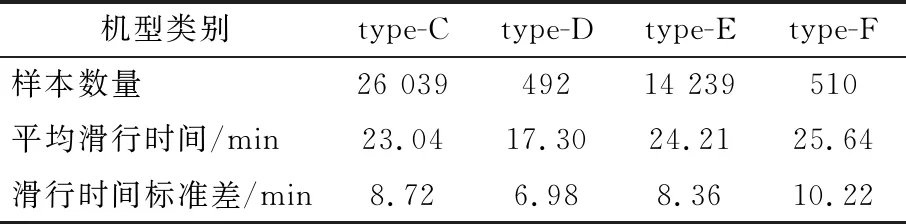
表2 各类机型样本数量、滑行时间均值及标准差
由表2可知,C类和E类机型为样本占比最大的两种机型,E类机型的平均滑行时间比C类机型长约1 min,且标准差相差很小,说明数据的离散程度相似.总体而言大机型的滑行时间普遍高于小机型,可见机型对滑行时间具有一定的影响.
为了让训练集涵盖更多的数据特征,使用one-hot编码将非数值型数据转化为数值型数据,机型变量就可以编码为一个长度为4的特征向量.每个航班有且仅有一种机型执飞,因此机型变量的约束条件为:
(2)
式中:FtypeC、FtypeD、FtypeE、FtypeF分别对应C、D、E、F四种机型;i为执飞的航班号.
5) 航空公司类别 一般而言,基地航司比非基地航司更熟悉场面环境,滑行速度相对更快;国内飞行员与管制对话时没有语言障碍,可以比外籍飞行员更快地执行指令,因此可以认为航空公司类型与滑出时间有一定的联系.从样本数、平均滑行时间和滑行时间标准差三个角度对国内航司、国外航司分别进行统计,结果见表3.可以看出国外航司执飞的航班占比近11%,在相同范围的滑行距离内,国外航司平均滑行时间比国内航司高出近2 min,可见航空公司类别不同对离港滑行时间具有一定影响,因此可将航空公司类别A分为国内和国外两种类型并设置为二值型变量,即当A=1时表示航班由国内航司执飞,A=0时表示航班由国外航司执飞.

表3 不同类别航空公司样本数、滑行时间均值及标准差
6) 机位影响指数 航空器的推出和滑行会占用推出引入线、机位资源和滑行道资源,导致周围其他机位上的航空器运行受限.受机坪构型等因素的影响,不同机位的飞机在推出滑行过程中影响的机位数量不同.受限机位数量越多,表明这个机位受其他机位的影响程度越大,因此对这个机位上航班的滑行时间影响也越大,因此将机位影响指数I也考虑进来.
基于上述分析,初步构建出了10个一次特征作为航空器离港滑行时间预测的初始特征集合,即X={D,Ntxot,Nins,tdep,FtypeC,FtypeD,FtypeE,FtypeF,A,I},其中特征Ntxot,Nins,A,I以及机型变量为本文首次提出.
1.2 二次特征构建
在特征工程中,运用两个特征的乘积就可以组成一对简单的交互特征,即二次特征.这种相乘关系可以用逻辑操作符AND来类比,表示由一对条件形成的结果,这种特征常见于决策树模型和广义线性模型中.除了采用离港飞机数量、机型等单独的特征来预测滑行时间,还可以将离港飞机数量和机型相乘,即根据某种机型的离港飞机数量来进行预测,通过构建此类二次变量捕获特征之间的交互作用.与仅使用单一特征相比,引入交互特征在一定程度上可能会为模型准确率的提升带来显著效果.
基于3.1的10个一次特征,可将它们分别两两相乘构建出一组二次特征.需要注意的是,在一次特征中机型类别为正交型特征,意味着它们之间两两相乘为0,因此需将这部分二次特征从候选集中剔除.此外,FtypeC,FtypeD,FtypeE,FtypeF,A这五个特征为二值变量,它的平方等于自身,因此也需将其从候选集中删除,所以一共可构建出44个二次特征.
本文构建二次特征基于以下两点原因:①在上述构建的10个一次特征中FtypeC,FtypeD,FtypeE,FtypeF,A分别为表征机型和航空公司类型的二值变量,这些二值特征和其他特征之间构成的交互特征可能会对模型产生重要的影响.②构建三次或更高次的特征会增加模型复杂度,容易导致模型过拟合,因此我们仅考虑构建二次特征.综上,候选特征集由一次特征、二次特征共同组成,共包含54个候选特征.
2 滑出模型设计
2.1 模型选择
为了选出合适的预测模型,使用K-最近邻(k-nearest neighbor,KNN)、支持向量回归(support vactor regression,SVR,包括Linear SVR、Poly SVR、RBF SVR)、决策树(decision tree)这几种常见的回归算法对54个候选特征进行初步试验,选取±3 min准确度、±5 min准确度、可决系数(R2)、均方误差(mean square error,MSE)、平均绝对误差(mean absolute error,MAE)、算法运行时间这6个指标对模型进行评估,结果见表4,决策树模型的预测效果在各项指标上的表现都更佳,此外决策树模型具备特征选择的功能可以去除冗余优化模型,因此选择决策树模型作为航空器离港滑行时间的预测模型.

表4 模型预测结果对比
2.2 决策树模型构建
CART树是决策树算法中用于解决回归问题的常见算法,CART树的生成是递归构建二叉决策树的过程,即每次划分都把当前样本集划分为两个子集,用误差平方和最小化准则进行特征选择.CART树回归算法具体如下:
假设X与Y分别为输入与输出变量,给定训练数据集
D={(x1,y1),(x1,y1),…,(xn,yn)}
(3)
选择第j个特征xj及其取值s作为切分变量和切分点,并定义两个区域R1和R2
(4)
步骤1遍历每一个特征及其每个取值,计算每个特征和切分点的损失函数,选择最小损失函数所对应的最优切分变量xj与切分点s,损失函数为
(5)
式中:cm为区间Rm上的输出平均值.
(6)
步骤2使用上步得到的切分点将当前的输入空间划分为R1和R2两个部分.
步骤3分别对两个子区域R1和R2递归调用步骤1~2,直到不能继续划分.
步骤4最终将输入空间划分为k个部分R1,R2,…,Rk,并且在每个部分Rk上有一个固定的输出值ck,那么回归树模型为
(7)
式中:I(x∈RK)为指示函数.
3 基于决策树的特征筛选
在机器学习的实际应用中,特征数量多、维度高容易引发“维度灾难”.本文构建的候选特征变量集中含有大量二维交互特征,增加了模型的训练时间和计算成本,因此特征选择具有十分重要的意义.具体而言,特征选择的目的是在不降低预测准确性或者在对预测准确性影响很小的情况下,从候选特征集中去除冗余和不相关特征,选择出能够构建一个简约模型的关键特征子集.通过精简无用的特征,可以降低模型的复杂程度、增强模型的泛化能力、提高计算效率.本文采用的决策树算法能够将特征选择作为模型训练的一部分,即在模型训练的同时自动进行特征选择.
3.1 最优特征集构建
以首都国际机场2019年10月10日—2020年1月2日36R跑道离港航班的实际运行数据作为样本数据集,采取随机抽样法进行划分,其中70%的数据作为训练集,其余30%作为测试集,训练集样本数为28 896,测试集样本数为12 384.
决策树的构建会针对每个特征计算出一个划分标准值,特征重要度为划分标准减少量的归一化值.CART回归树的特征重要度是误差平方和减少量的归一化值,公式为
(8)
式中:N为样本的总数;Nt为当前节点的样本数目;NtL为结点左子树的样本数目;NtR为结点右子树的样本数目;impurity为不纯度,这里指的是误差平方和;right_impurity为结点右子树的不纯度;left_impurity为结点左子树的不纯度.特征越重要,不纯度就越小;不纯度减小得越多,意味着该结点分裂的收益越大,该节点对应特征的重要度越高.
特征重要度反映了各个特征在模型构建中对目标变量预测的贡献能力,特征重要度越大说明对目标变量预测的贡献能力越强.将重要度由大到小排序,表5为重要度排名前10位的特征,采用序列前向选择算法进行特征筛选,即从空集开始依据重要度排名由高到低依次将特征加入特征子集,接着重新训练模型,然后依据预测准确率最高的原则选择最优的特征子集.图3为不同特征子集训练出的模型所对应的平均绝对误差(mean absolute error,MAE),横轴为每次用于模型训练的特征个数.

表5 特征重要度(前10位)
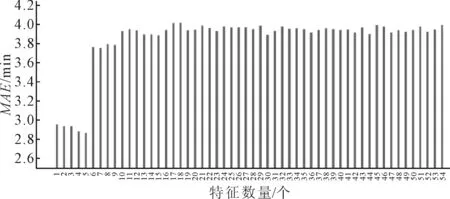
图3 特征筛选迭代过程
由图3迭代的结果可以看出,当添加5个特征变量时,平均绝对误差最小,当继续添加特征变量时,预测误差在不断变大.由此可以认为这5个特征变量构成的特征子集是决策树模型的关键特征子集,不仅可以提升模型的准确度,同时大大降低了模型的复杂程度,提高了计算效率.因此,本文构建的最优特征变量集为
最优特征变量集由4个二次特征和1个一次特征组成,可以看出通过决策树算法对特征变量进行筛选后,从10个候选一次特征中选出了4个一次特征,即Ntxot、Nins、A和FtypeC,这4个二次特征均与Ntxot有关,说明拥堵变量对滑行时间特征选择具有十分重要的影响.

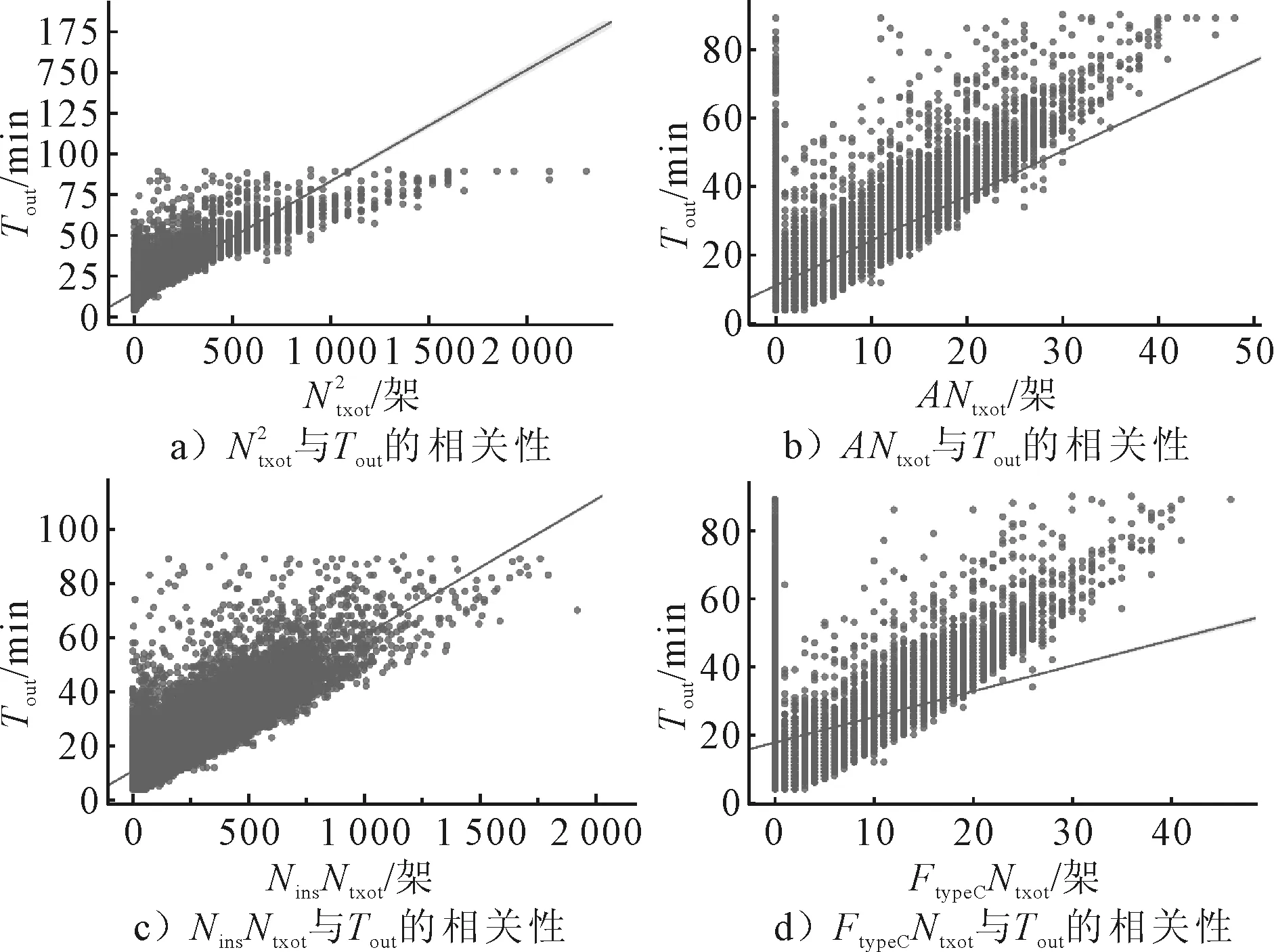
图4 最优二次特征和滑出时间的相关性分析
3.2 结果分析
对筛选出的五个交互特征的各项指标进行交叉验证,对比使用筛选出的五个交互特征构建的模型和单独使用一次特征构建的模型的性能指标见表6,与单独采用一次特征相比,引入交互特征预测离港滑行时间可使准确率有较大的提升.图5为滑行时间预测值与实际值的对比图,横轴为测试集样本,纵轴为离港滑行时间的预测值和真实值,可见预测值能较好得拟合真实值的变化情况,再次验证本文采用的方法具有较好的预测效果.
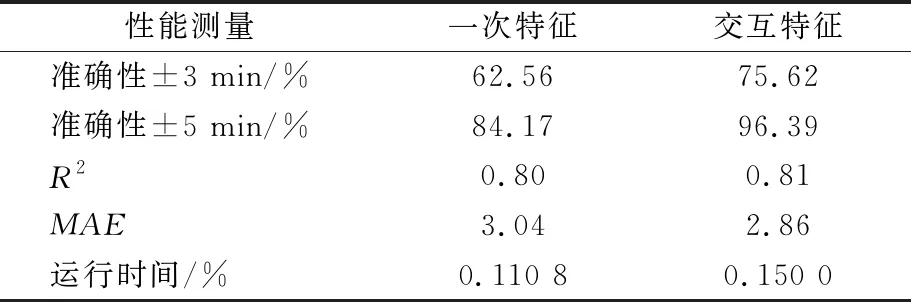
表6 预测结果对比

图5 预测结果对比图
4 结 论
1) 提出进离港瞬时流量、机型、航空公司等因素对离港滑行时间的影响,并将这些影响因素构建成一次特征作为预测模型的输入,取得了良好的效果.
2) 运用特征工程构建交互特征,验证了二值特征和其他特征之间的交互作用对预测模型产生的重要影响.
3) 采用决策树模型进行特征筛选构建最优特征子集,在降低模型复杂度的同时提升了预测的准确度.
4) 与直接采用单独的一次特征构建预测模型的传统做法相比,本文引入交互特征的方法使模型具有更好的预测准确率、R2和MAE.
