循环神经网络在结构损伤识别中的应用研究

2021-07-07王子凡张健飞

河南科学 2021年6期

王子凡，张健飞

（河海大学力学与材料学院，南京 211100）

随着经济社会的发展，我国兴建了一大批重大工程结构，这些工程结构在服役的过程中，由于多种因素的影响，其结构损伤不可避免.为了不影响工程结构的安全使用，准确有效地检测工程结构损伤尤为重要.传统的结构损伤检测技术有一定的局限性，而基于结构动态响应的结构损伤检测技术是利用采集到的振动信息，对发生在结构上的损伤进行检测，不仅不影响结构的正常使用，而且成本较低，克服了传统检测技术的缺点.结构振动信息包括时序信息和模态域信息，时序信息主要包括位移、加速度等，模态域信息主要包括频率、振型、模态应变能等.目前，使用模态域数据进行损伤识别是一种比较常见的方法，该方法首先根据振动响应数据来识别结构的模态参数，然后比较结构损伤前后的模态参数［1］，或是利用神经网络［2］及模型修正［3］等方法进行损伤检测，但是由于很多模态域数据对损伤不敏感，故该方法有其局限性.而大多数基于时序数据的结构损伤识别方法是利用时间序列分析模型提取结构振动响应在时间域上的特征来识别结构损伤的［4］，这些方法使用的是直接测得的时序数据，不需要进行各种转换，结构响应中与损伤有关的特征不会产生数值误差，所以其优势相对更加突出.

近年来，随着深度学习的不断发展，一些深度学习的模型，如卷积神经网络、循环神经网络等，也被应用到基于时序数据的异常检测之中.2016年，Kiranyaz等［5］首次利用一维卷积神经网络对病人特定情况下的心电图进行分类检测，其结果表明卷积神经网络在心室异位搏动和室上异位搏动的检测上具有很好的分类性能，其分类准确率分别为99%、97.6%.陈伟等［6］使用随机搜索和长短期记忆（Long Short-Term Memory，LSTM）循环神经网络对滚动轴承故障识别的研究表明，这种模型的诊断准确度可以达到99.8%以上，与支持向量回归机、粒子群算法最小二乘支持向量机等典型时间序列预测模型相比，在拟合和预测性能方面具有更高的准确度.结构损伤检测的深度学习模型目前主要集中于卷积神经网络.张盼盼等［7］建立了卷积神经网络（Convolutional Neural Network，CNN）薄板损伤识别模型，其结果表明卷积神经网络在噪声环境下具有良好的识别能力.汪洋等［8］提出了一种基于CNN和门控循环单元（Gated Recurren Unit，GRU）神经网络的减速机轴承故障诊断方法，结果表明其故障识别率可以达到94%以上，具有较强的泛化能力.Abdeljaber等［9］将卷积神经网络用于看台模拟器的损伤检测，利用卷积神经网络分析其振动信号，结果表明卷积神经网络在实时监测计算时具有良好的效率.

本文对循环神经网络在结构损伤识别中的应用进行了研究，首先利用循环神经网络直接提取结构加速度时序数据中的特征进行损伤识别；然后基于某重力坝有限元模型生成的不同噪声水平的加速度数据对循环神经网络进行训练和测试；最后采用网格搜索和随机搜索两种方法对循环神经网络的超参数进行优化，并比较了这两种方法的优缺点.

图1 RNN细胞结构Fig.1 RNN cell structure

1 循环神经网络

循环神经网络（Recurrent Neural Network，RNN）是一种增加了由自身的本时刻输出指向下一时刻输入的循环连接的人工神经网络［10］，其通过新的连接方式将时间序列的概念引进到网络结构的设计中.RNN的结构决定了其可以利用时间序列的历史信息对时序数据建模以进行序列识别以及预测.一个基础的RNN包含输入层、隐藏层和输出层.图1展示了一个RNN隐藏层细胞结构.

图1中：输入至输入层的是一段关于时间t的向量(…,xt-1,xt,xt+1,…)，其中xt=(x1,x2,…,xN)，t≥1；f为激活函数；ht为t时刻隐藏层输出序列；ht-1为t-1时刻指向t时刻的隐藏层输出序列；yt为t时刻输出层输出序列.

t时刻隐藏层及输出层序列的计算方法如式（1）和式（2）所示.

式中：fh为隐藏层激活函数；Wxh为输入数据至隐藏层的权重矩阵；Whh为当前时刻隐藏层至下一时刻隐藏层的权重矩阵；bh为隐藏层偏置.

式中：fy为输出层激活函数；Who为隐藏层至输出层的权重矩阵；by为输出层偏置.

因为RNN中存在梯度爆炸和梯度消失的问题［11］，所以RNN在长期学习方面表现十分薄弱，为了解决这个问题，Hochreiter等［11］在1977年首次提出了长短期记忆（LSTM）循环神经网络.LSTM循环神经网络可以有效解决梯度爆炸及梯度消失问题，使得循环神经网络能够真正有效地利用长距离的时序数据.LSTM循环神经网络已经被大量用于序列学习相关的任务中，比如语音识别［12-13］、语言模型［14-15］等.LSTM循环神经网络使用了记忆细胞来代替一般循环神经网络中的隐藏层细胞，有效解决了梯度爆炸及梯度消失问题，记忆细胞的输入和输出都由一些门控单元来控制，这些门控单元控制流向隐藏层单元的信息，遗忘门决定从上一个细胞状态中丢弃什么信息，输入门将新的信息选择性的记录至细胞状态中，输出门将信息传递出去.经过长时间的演化，目前应用最为广泛的LSTM循环神经网络单元结构如图2所示.

图2中：i、f、c、o、h分别代表输入门、遗忘门、细胞状态、输出门以及隐藏层输出序列；t表示时刻（举例来说，即ct表示t时刻的细胞状态输出序列，ct-1即为t-1时刻的细胞状态输出序列，xt为t时刻的输入层输入序列，yt为t时刻输出层输出序列）；σ为sigmoid函数；tanh为双曲正切激活函数.

t时刻输入门输出序列的计算方法如式（3）所示：

图2 LSTM循环神经网络细胞结构Fig.2 Cell structure of LSTM recurrent neural network

式（3）中：Wxi表示输入数据到输入门的权重矩阵；Whi表示上一时刻隐藏层至本时刻输入门的权重矩阵；Wci表示上一时刻细胞状态至本时刻输入门的权重矩阵；bi为输入门的偏置.

t时刻遗忘门输出序列的计算方法如式（4）所示：

式（4）中：Wxf表示输入数据到遗忘门的权重矩阵；Whf表示上一时刻隐藏层至本时刻遗忘门的权重矩阵；Wcf表示上一时刻细胞状态至本时刻遗忘门的权重矩阵；bf为遗忘门的偏置.

t时刻细胞状态输出序列的计算方法如式（5）所示：

式（5）中：Wxc表示输入数据至细胞状态的权重矩阵；Whc表示上一时刻隐藏层至本时刻细胞状态的权重矩阵；bc为细胞状态的偏置.

t时刻输出门输出序列的计算方法如式（6）所示：

式（6）中：Wxo表示输入数据至输出门的权重矩阵；Who表示上一时刻隐藏层至本时刻输出门的权重矩阵；Wco表示上一时刻细胞状态至本时刻输出门的权重矩阵；bo为输出门的偏置.

最终t时刻隐藏层输出序列的计算方法如式（7）所示：

sigmoid函数σ(x)与双曲正切激活函数tanh(x)如式（8）与式（9）所示，x表示待激活的序列：

图3 GRU神经网络细胞结构Fig.3 Cell structure of GRU neural network

除此之外，LSTM循环神经网络也有很多改进网络，门控循环单元（Gated Recurrent Unit，GRU）神经网络是其中比较成功的一种［16］.GRU神经网络在保持LSTM循环神经网络效果的基础上精简了结构，减少了超参数的数量.相比LSTM循环神经网络的三种门控单元，GRU神经网络使用更新门和重置门来达到相似的效果，更新门用于控制前一个时间步的信息被带入当前状态的程度，重置门用于控制舍弃前一个时间步信息的程度.GRU神经网络单元结构如图3所示.

图3中：r、z、hˉ、h分别代表重置门输出序列、更新门输出序列、隐藏层预备输出序列以及隐藏层输出序列；xt为t时刻输入层输入序列；yt为t时刻输出层输出序列；t表示时刻；σ为sigmoid函数；tanh为双曲正切激活函数.

t时刻重置门输出序的列计算方法如式（10）所示：

式（10）中：Wxr表示输入数据至重置门的权重矩阵；Whr表示上一时刻隐藏层至本时刻重置门的权重矩阵.

t时刻更新门输出序列的计算方法如式（11）所示：

式（11）中：Wxz表示输入数据至更新门的权重矩阵；Whz表示上一时刻隐藏层至本时刻更新门的权重矩阵.

t时刻隐藏层预备输出序列的计算方法如式（12）所示：

式（12）中：Wrh表示重置门至更新门的权重矩阵；Wxh为输入数据至隐藏层的权重矩阵.

最终t时刻隐藏层输出序列的计算方法如式（13）所示：

样本序列在输入至三种循环神经网络隐藏层细胞后，经过对数据特征的提取和传递，通过最后一个细胞将结果输出至输出层.输出层后加入全连接层，用以损伤工况的识别分类.在本文中，全连接层使用激活函数Softmax函数，这个函数的作用就是将每个损伤类别所对应的输出序列归一化，其计算如式（14）所示.

式（14）中：yi、yj分别为神经网络的全连接层输出序列{y1,y2,…,yi,…,yj,…,yn}这n个分量中的一个，它们分别对应一种损伤工况，n≥2.

本文的损失函数选择用于多分类的交叉熵损失函数［17］，即在Softmax函数将神经网络的输出序列变成一个概率分布后，通过交叉熵损失函数来计算预测的概率分布和实际的概率分布之间的距离，其值为无量纲.计算方法如式（15）所示，其所计算出来的损失值J越低越好.

式中：K为多分类的种类数量，此处为损伤工况数；p为真实概率，如果损伤类别是i，则pi=1，否则为0；y′i为经由式（14）所示的Softmax函数计算得来的输出值，即损伤工况i的预测概率.

2 数值实验

2.1 实验数据

训练和测试数据均采用某重力坝的二维有限元模型生成，坝底施加水平向和垂直向的白噪声加速度以模拟环境激励下的坝体动力响应，计算时间步长为0.005 s，采用Rayleigh阻尼.考虑到重力坝上游面深层水平裂缝比较常见且具有较大的危害性［18］，本文在坝体上游面不同高程处设置一条深2 m的水平裂缝以模拟不同位置的损伤，下游面设置10个测点测量坝体水平向加速度，坝体有限元网格、测点位置和裂缝位置如图4所示，不同工况如表1所示.坝体加速度信号采样频率为200 Hz，共生成时长为250 s的9组不同损伤位置（含无损伤）的训练集数据，将其中20%划分为验证集，每条数据由10个测点数据以及标签组成，每组工况共生成5万条数据，以及时长为20 s的测试集数据.

图4 有限元网络、测点位置和裂缝位置Fig.4 Finite element grid，measuring point location and crack location

表1 不同工况设置Tab.1 The setting of different working conditions

2.2 不同循环神经网络的比较

为了对比三种不同循环神经网络的性能，在相同数据集以及相同超参数组合下，将三种循环神经网络迭代200次进行比较，实验结果如图5及表2所示，表中准确率保留一位小数，损失值保留两位小数.由表2可以看出，与其他两种循环神经网络相比，LSTM循环神经网络对所有工况的识别准确率均比RNN以及GRU神经网络高，其中对工况1、工况2和工况3的识别准确率均达到了100%.LSTM循环神经网络对于工况0的识别准确率比GRU神经网络高14.4%，比RNN高46.5%；LSTM循环神经网络的验证集识别准确率比GRU神经网络高2.2%，比RNN高36.1%.根据图5可知，GRU神经网络和LSTM循环神经网络的损失曲线趋势较为相似，LSTM循环神经网络损失值最低下探至0.29，GRU神经网络的损失值最低下探至0.21，RNN的损失值最低下探至0.77.LSTM循环神经网络的耗时均多于另外两种循环神经网络，主要是由于LSTM循环神经网络所需要训练的超参数数量更多，网络结构更为复杂.综合来看，在三种循环神经网络中，LSTM循环神经网络的综合性能与RNN相比提升很大，与GRU神经网络相比略有提升.

表2 三种循环神经网络的准确率和损失值对比Tab.2 Comparison of accuracy rates and loss values of three kinds of recurrent neural networks

图5 相同参数下三种循环神经网络的验证集识别准确率和损失值对比Fig.5 Comparison of verification set identification accuracy rates and loss values of three kinds of recurrent neural networks under the same parameters

2.3 超参数优选

在本文2.2小节中，循环神经网络训练所涉及的超参数是根据经验选取的，为了达到更好的效果，本文选择综合性能更优的LSTM循环神经网络作为优化对象，采取优化算法对超参数进行优选.LSTM循环神经网络的超参数优选主要集中于3个超参数：样本长度L，前馈网络层隐藏神经元数量，又称状态向量大小Sstate以及控制网络调参幅度的学习率η.使用网格搜索及随机搜索对其进行优化.网格搜索根据超参数的个数来确定网格搜索的空间维度，在每个维度上划分网格，然后遍历所有的网格交叉点，根据网格交叉点所给出的结果来确定最佳超参数.相比于其他的超参数优化方法（比如粒子群算法、蚁群算法等），这种方法更简单实用［19］.网格搜索的搜索过程主要分为三步：首先将重要性较低的超参数固定，比如网络迭代的次数epochs，在本文的搜索过程中，迭代次数取值100；接着设定3个超参数的取值范围，学习率η∈｛0.000 1，0.001，0.01｝，样本长度L∈｛200，150，100，50，20｝，状态向量大小Sstate∈｛16，32，48，64｝；最后，将目标函数LSTM循环神经网络测试集的识别准确率设置为最高.表3给出了每一个网格交叉点对应的超参数组合构建的LSTM循环神经网络在测试集上的识别准确率，结果保留一位小数.

由表3可以看出，在相同的学习率及样本长度下，状态向量大小为48或64时，LSTM循环神经网络更容易获得较高的识别准确率；样本长度在100或是150时，LSTM循环神经网络的测试集识别准确率最高，表明分类的效果相对最好.学习率为0.001时，所获得的LSTM循环神经网络分类的效果最好；学习率为0.000 1时，LSTM循环神经网络的测试集识别准确率较低，这是由于过小的学习率导致损失函数的变化很慢，使得LSTM循环神经网络很容易困在局部最小值点.

在选定了优化超参数后，选择排名第一的最优超参数，使其充分迭代200次，200次迭代后LSTM循环神经网络测试集的识别准确率最高可达到98.1%，损失值最低下探至0.114 7，与根据经验选择的超参数组合相比，准确率大大提升.

网格搜索带来的一个明显问题是，计算代价会随着超参数数量的增多而成指数倍增长，很浪费计算资源，因此，随机搜索应运而生.随机搜索与网格搜索不同，搜索空间可以不是离散的，这就允许随机搜索在同样的计算资源下尝试更多的超参数组合［20］，如图6所示.

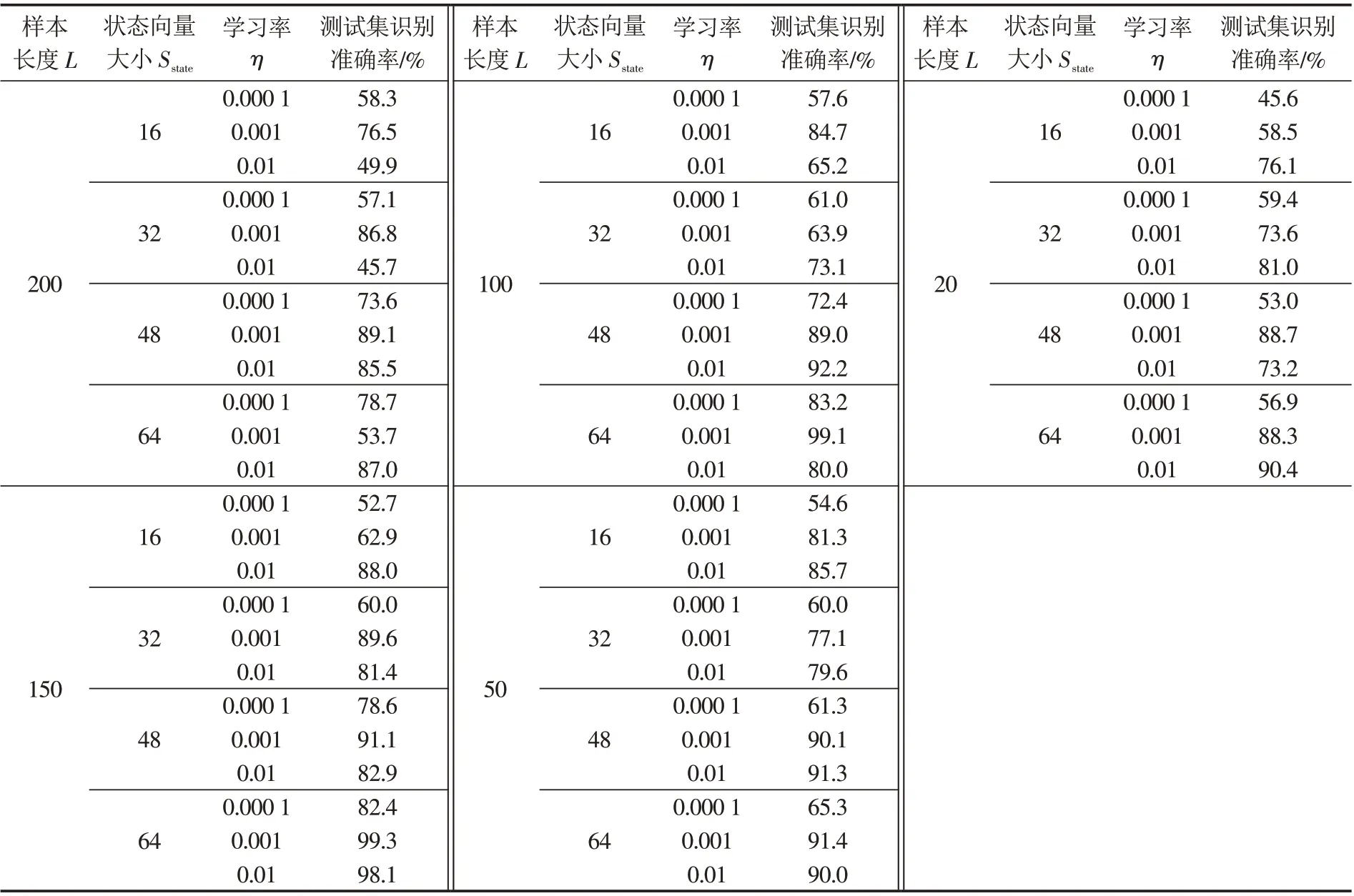
表3 网格搜索结果Tab.3 The results of grid search

图6直观地阐述了网格搜索和随机搜索的不同.图中横轴代表对网络性能影响更大的重要超参数，纵轴为影响较小的不重要超参数.由图6可以看出在搜索相同次数的情况下，网格搜索将大量的计算资源浪费在了对网络性能影响不大的超参数中，而随机搜索几乎每一次都测试了对结果有影响的每个超参数独一无二的值，也就是说，随机搜索尝试了更多有益的超参数组合.

使用随机搜索对相同的三个超参数进行搜索，三个超参数的取值范围为：η∈（0.000 1，0.01），L∈（20，200），Sstate∈（16，64）.搜索完成后使用搜索出的超参数构建LSTM循环神经网络，迭代200次.将使用随机搜索得出的迭代结果与使用网格搜索得出的迭代结果进行对比，如表4所示.