RV减速器行星轮系齿形修形传动啮合性能分析

王佳, 娄军强, 李国平*, 罗利敏, 励 晨

RV减速器行星轮系齿形修形传动啮合性能分析

（1.宁波大学 浙江省零件轧制成形技术研究重点实验室, 浙江 宁波 315211;2.宁波中大力德智能传动股份有限公司, 浙江 宁波 315301）

为准确掌握齿形修形对RV-150BX减速器行星轮系动态啮合性能及传动性能的影响, 建立了行星轮系装配模型, 通过有限元法分析了输入轴齿轮和行星轮在动态啮合中的传动规律, 在啮合临界时刻最大和最小等效应力分别为14.47MPa和8.55MPa. 经综合考虑, 选取输入轴齿轮和行星轮齿顶修形量优化设计参数; 通过动态啮合仿真, 分析同等载荷下齿形修形后的传动性能. 结果表明, 在轮齿单、双齿交替啮合时刻, 齿轮的速度、加速度波动最大并伴随冲击振动. 经比较发现, 齿形修形后速度、加速度波动明显改善, 传动性能显著提高.

RV减速器; 行星轮系; 动态啮合; 齿形修形; 有限元法

旋转矢量(Rotary Vector, RV)减速器作为精密传动装置是由初级渐开线行星传动和次级摆线针轮行星传动串联而成[1]. RV减速器具有传动比大、刚度高、运动平稳且传动精度高等优点, 被广泛应用于工业机器人、机床和高端医疗设备等领域[2]. 由于RV减速器结构属于多级过约束机构, 导致其受力情况较为复杂, 国内外学者对其两级传动轮系的静、动力学问题进行了大量研究. 刘伯希等[3]利用集中参数法建立了摆线轮扭转动力学模型, 并通过自由振动方程求解得出偏心角度对系统固有频率的影响, 轮齿修形可减轻齿轮的冲击振动和噪声, 减小动载荷, 改善传动性能. Wang等[4]提出了一种RV减速器多齿接触模型, 研究了载荷变化对于不同修形方法的影响. 张大卫等[5]基于Hertz公式和石川公式, 建立了RV减速器摆渐开线行星齿轮传动副的啮合刚度模型, 并通过动特性试验进行了有效性验证. Wang[6]利用齿面接触分析(Tooth Contact Analysis, TCA)和承载齿面接触分析(Loaded Tooth Contact Analysis, LTCA)模拟了齿轮动态啮合过程, 提出一种齿轮三维减振修形方法. Li等[7]在建立齿轮传动三维动态啮合模型的基础上, 采用有限元法和田口方法分析了齿廓偏差、啮合误差和齿顶修形对齿面接触应力的影响. 然而,在实际中齿面承载能力和啮合刚度并不是衡量修形结果和传动啮合性能的唯一依据, 除了要考虑承载能力和疲劳强度外, 还需要关注修形后传动啮合的平稳性. 通常啮合传动的平稳性可以从齿轮速度和加速度变化得以反映. 平稳性不足的齿轮在实际工作中会出现噪声和振动, 而控制修形量可以有效改善这一状况, 提高传动啮合性能.

本文根据渐开线行星齿轮组的传动特点, 利用有限元法对修形前后的齿轮进行运动和受力状态(包括应力状态、速度及加速度变化)分析, 以优化RV减速器动态啮合传动性能和传动效率, 以期为轮齿修形设计及分析提供依据.

1 RV减速器工作原理

RV减速器以摆线轮行星传动为基础, 是一种二级封闭式、少差齿行星传动机构. 相较于传统减速器, RV减速器具有传动比大、精度高、体积小且重量轻等优点[8]. 本文以宁波中大力德智能传动股份有限公司的RV-150BX型号减速器(以下简称RV-150BX减速器)为例. RV-150BX减速器结构如图1所示, 依次由油封、输入行星架、主轴承、针齿壳、行星轮、输入轴、摆线轮、曲柄轴、主轴承和输出行星架等组成.

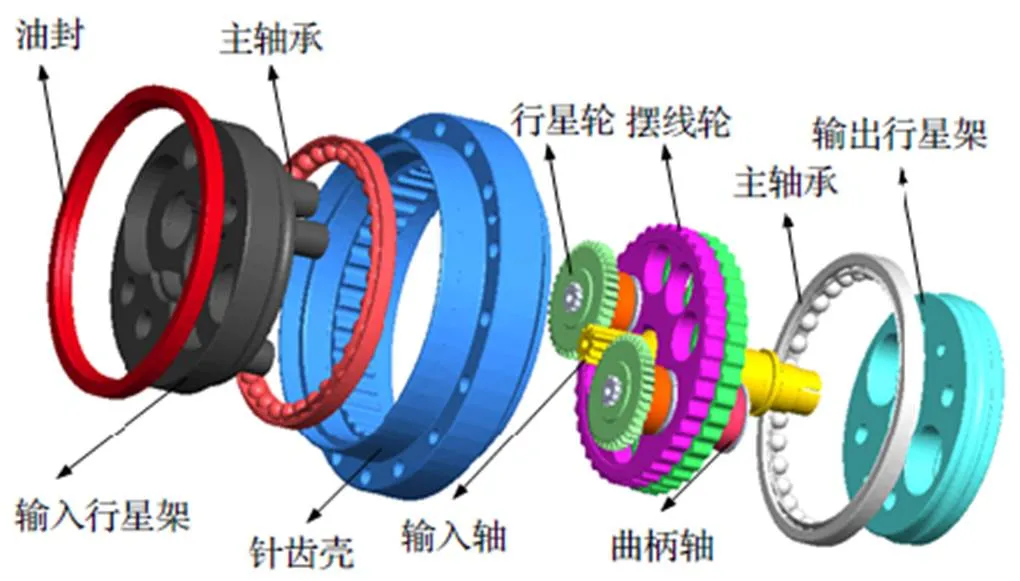
图1 RV减速器结构示意图

RV减速器的一级减速部分由输入轴齿轮和行星轮组成, 其工作原理如图2所示. 伺服电机通过联轴器作用于输入轴, 输入轴齿轮和行星轮啮合传递动力. 二级减速部分主要由摆线轮、针齿、针齿壳组成, 行星轮和曲柄轴同速转动带动摆线轮做偏心转动, 实现摆线轮与针齿、针齿壳啮合, 最终由行星架输出动力[9].

图2 RV减速器传动原理图

2 RV减速器一级减速系统动态啮合分析

在RV减速器传动过程中, 行星轮和输入轴组成的一级减速部分啮合频率较高, 同时输入轴和外部驱动电机相连接, 起到传递转矩的作用. 因此行星轮齿根疲劳断裂及齿面磨损是其工作过程中主要的失效形式.

以RV-150BX减速器为例, 首先在直角坐标系下建立输入轴齿轮以及与之啮合的行星齿轮的渐开线方程. 通过绘制样条曲线生成输入轴齿轮与行星轮齿的渐开线齿廓, 并建立模型. 直角坐标系下的渐开线齿廓方程可表示为:

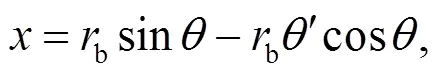
RV-150BX减速器输入轴齿轮及行星轮的基本尺寸参数见表1. 取输入轴齿轮有效齿长为齿宽, 简化其螺孔、内花键等特征, 按照实际中心距对生成的输入轴齿轮和行星轮进行装配.

表1 输入轴齿轮及行星轮参数

RV减速器的一级传动部分轮齿啮合可视作渐开线直齿轮啮合. 为了降低齿轮啮合瞬态动力学中的计算量, 需对模型和条件设置进行优化. 网格依据装配体部件不同位置进行划分, 对参与啮合接触的轮齿进行细化, 其余位置降低网格要求. 采用Soild186单元, 六面体网格划分, 共划分出网格单元130448个, 节点25208个, 装配体模型及其网格如图3所示.

图3 输入轴齿轮与行星轮网格模型

输入轴齿轮与行星轮相连并添加转动副和接触对, 其中输入轴齿轮齿面为接触面, 行星轮齿面为目标面, 接触对摩擦系数为0.1, 限制齿轮内圈自由度, 令其仅可绕轴转动. 在输入轴齿轮转动副中输入转速为60rad·min-1, 行星轮转动副添加负载转矩为500N·mm, 设置总运行时间2.2s.等效应力集中在齿根处, 一般采用等效应力或正应力来描述齿轮弯曲应力, 以反映齿轮齿根部位抗疲劳折断能力.

直齿轮的弯曲疲劳强度可表示为[10]:

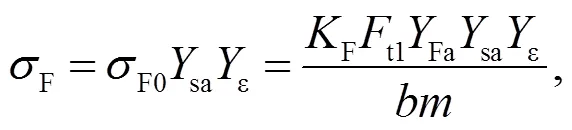
式中:sa为应力修正系数;ε为重合度系数;F为载荷系数;t1为分度圆处的径向力;Fa为弯曲疲劳强度的载荷系数;为齿宽;为模数.

重合度系数ε及重合度ɑ的计算公式为:

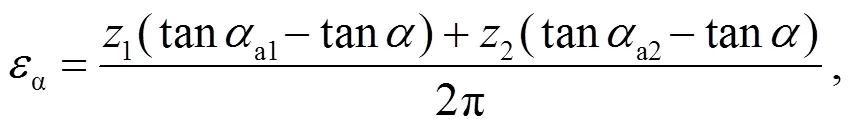
根据文中参数, 由理论计算可得齿根弯曲应力为14.753MPa, 重合度为1.3612.

对仿真结果进行分析, 输入轴齿轮齿宽远大于行星轮, 行星轮的最大等效应力曲线值大于输入轴齿轮, 得到行星齿轮冯·米塞斯(von Mises)等效应力变化曲线. 取2个稳定周期内应力变化曲线, 如图4所示.

从图4可知, 齿轮交替啮合时等效应力发生周期变化, 其中一个完整周期内各临界位置的应力变化如图5所示.

图4 齿轮交替啮合等效应力曲线

图5(a)为0.16s时齿轮的啮合情况, 此时齿轮正进入双齿啮合, 最大等效应力发生在上齿对的齿根侧, 应力值为9.80MPa, 约为最大等效应力的2/3. 图5(b)为0.26s时齿轮的啮合情况, 此时两对齿轮共同分配载荷, 应力最小, 为8.55MPa. 图5(c)为0.36s时齿轮的啮合情况, 此时齿轮正从双齿啮合进入单齿啮合, 等效应力急剧上升至最大, 应力约为14.47MPa, 由单对轮齿承担载荷. 图5(d)为0.68s时齿轮的啮合情况, 此时齿轮从单齿啮合进入双齿啮合, 在单齿啮合单区间内, 啮合点不断向齿轮中部移动, 应力逐渐降低, 从0.68s进入下一周期. 此等效应力曲线和各临界位置的等效应力可以较好地反映周期内齿轮啮合的动态过程.

图5 齿轮啮合状态下各临界位置的等效应力

3 齿顶修形后传动性能分析比较

齿轮传递动力时, 轮齿部犹如受动载荷的悬臂梁, 轮齿啮合的刚性周期性变换导致轮齿弹性变形, 故齿轮实际啮合点并非总处在啮合线上, 被动齿轮的运动滞后于主动齿轮的运动, 其瞬时速度差会造成啮合干涉和冲击, 产生振动和噪音. 为了提高齿轮传动的平稳性, 降低动载荷和噪声, 通常需要对齿轮进行修形. 常见的齿轮修形有齿顶修正、修缘、修根、挖根、曲面修整、修正齿形角等, 修形可以改善齿面的润滑状态, 缓解和防止胶合破坏, 改善传动性能[11-12].

齿轮的齿顶和齿根是参与交替啮合、传动的重要对象. 在齿轮制造中, 对于齿数小于17齿的齿轮, 为防止根切, 常对其采取正变位, 若正变位过大, 齿轮的齿顶变尖, 齿顶厚度薄, 导致齿轮的齿顶部分在啮合传动时强度低、刚性差, 影响齿轮平稳传动[13]. 另外, 在啮合时齿顶、齿根处啮合滑动率最大, 尖锐的齿顶容易造成齿面磨损. 在实际应用中, 采用齿顶修正可以优化这一现象. 但齿顶修正后的齿轮重合度会变小, 因此对齿轮修形量需要进行有效控制. RV-150BX减速器输入轴齿轮的齿数和行星轮的齿数均较小, 需考虑对齿形进行修形, 以提高啮合的传动性能. 采用齿顶修正后对齿轮的齿顶再进行倒角, 修形位置如图6所示. 对于大小轮齿分别控制修形量为齿顶高约5.0%和7.4%, 修形量参数见表2和表3.

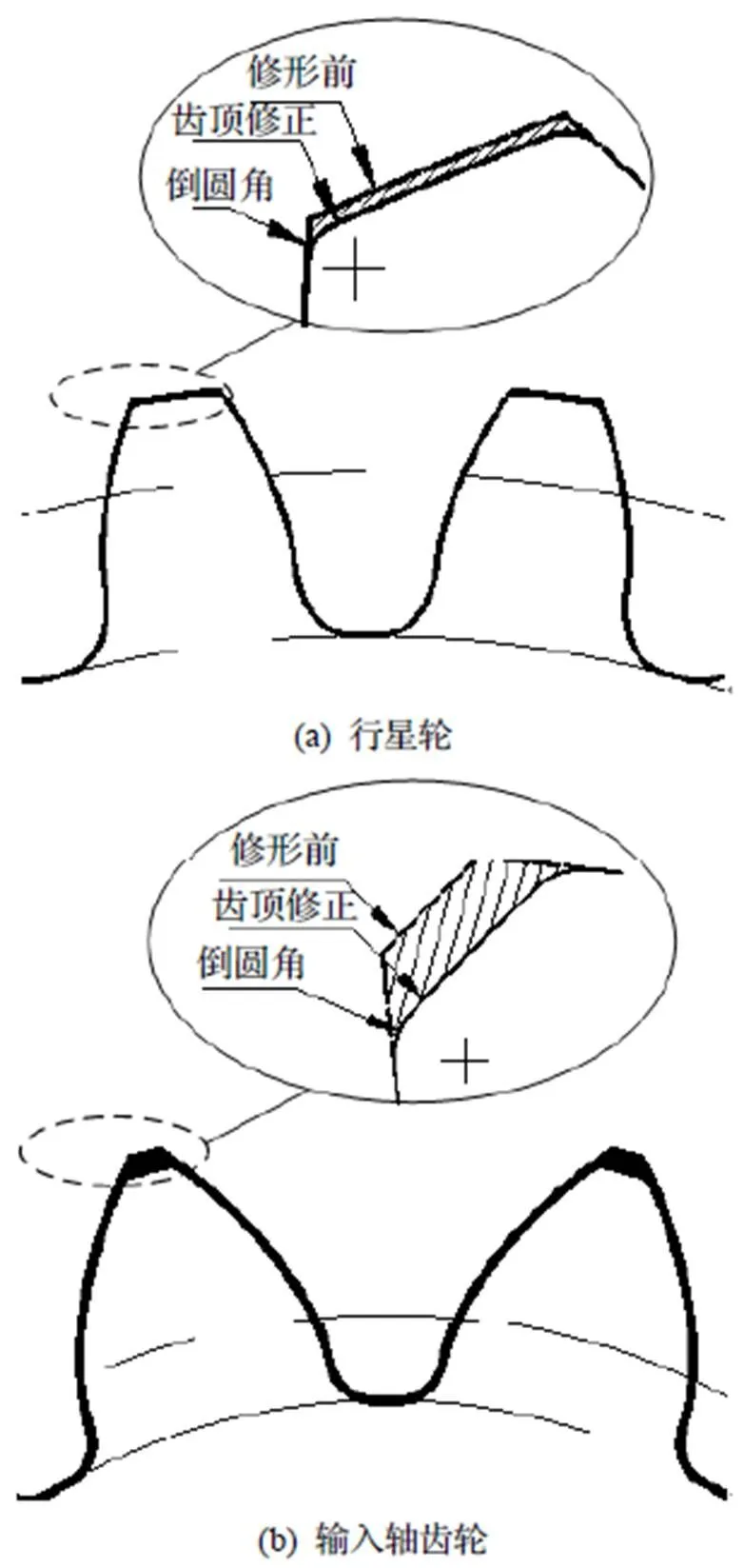
图6 输入轴齿轮和行星轮修形

表2 行星轮修形量参数

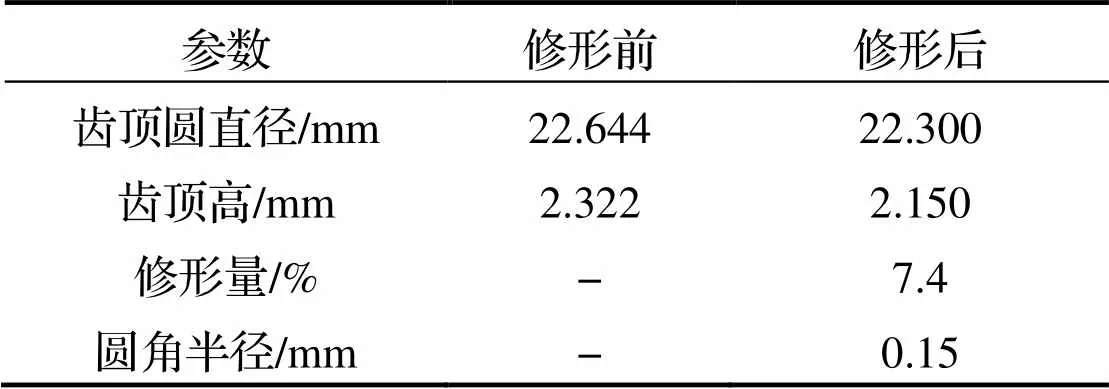
表3 输入轴齿轮修形量参数

分析修形后初级行星减速传动轮系啮合瞬态动力学特性, 并比较修形前后的传动性能.

图7为修形前后的等效应力. 从图7可知, 修形前后等效应力变化趋势一致, 修形后最大等效应力约为修形前的103%. 由于齿轮修形后齿顶材料被去除了一部分, 其对载荷的承载能力下降, 最大应力略有增大, 增量对整体疲劳强度影响较低. 修形后齿轮啮合重合度下降, 单齿啮合区间增大, 双齿啮合的齿对提前进入单齿啮合. 因此, 进行齿顶修正时需要正确控制修形量, 防止重合度过小, 影响齿轮承载性能和传动性能.

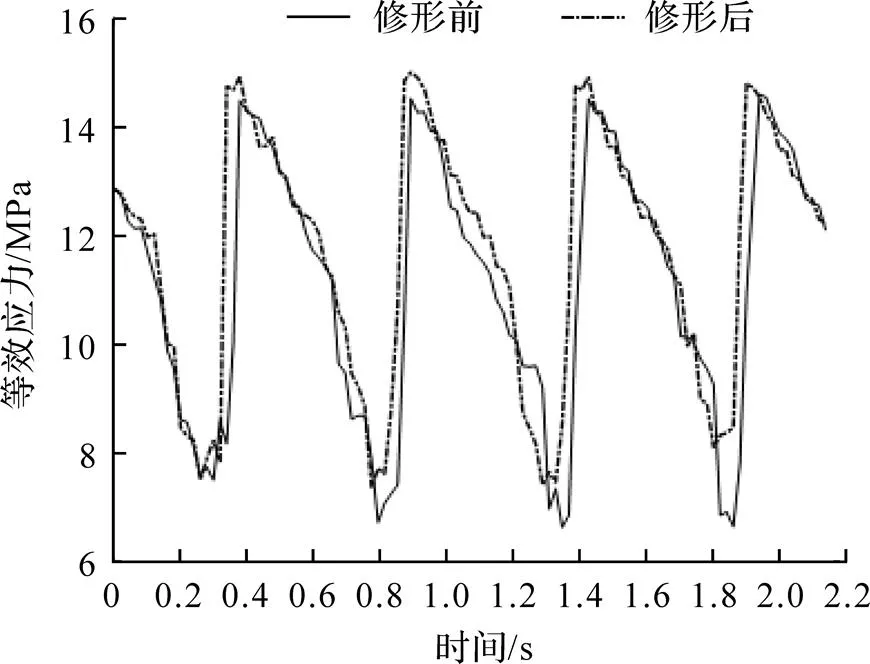
图7 修形前后等效应力比较

修形前后最大速度变化曲线如图8所示, 曲线表示行星轮在加速启动至平稳运行时的速度规律. 结合图7可以得到齿轮在一个完整周期内共发生2次速度变化, 分别发生在单、双齿交替啮合时刻, 其中由单齿啮合进入双齿啮合时速度波动较小, 由双齿啮合进入单齿啮合时速度波动较大, 此时也伴随较大的振动和冲击. 随着齿轮啮合, 速度波动减弱, 突变波动幅度变小. 比较修形前后的速度波动, 修形后较修形前速度波动更小, 传动更加稳定, 单齿啮合和双齿啮合区间都有明显改善, 传动平稳性提高.

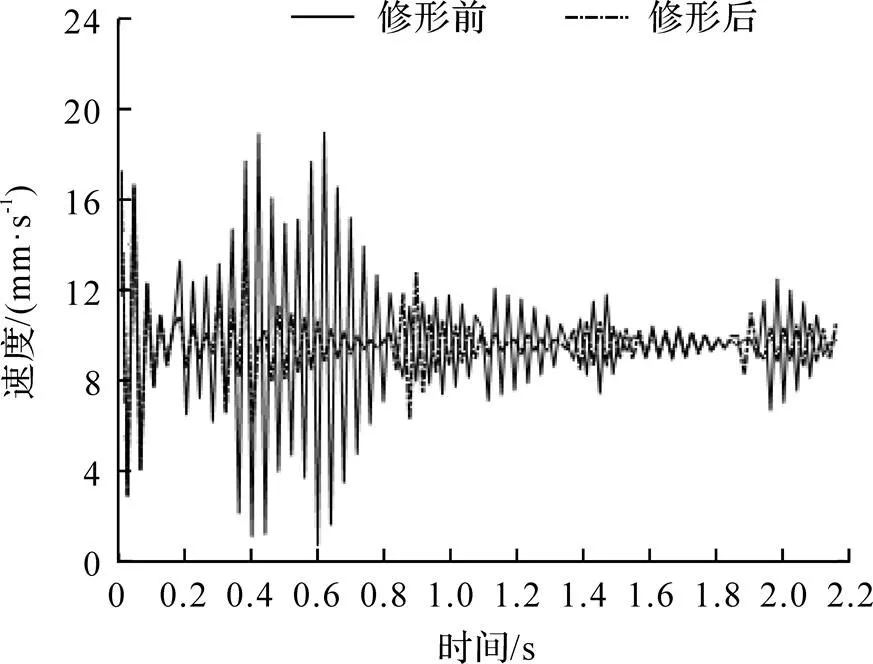
图8 修形前后速度曲线比较

图9为修形前后加速度变化的比较. 从图9可知, 行星轮在加速启动至平稳运行时其加速度变化趋势修形前后基本一致, 在单、双齿交替啮合时刻均会发生加速度突变. 修形后加速度突变改善明显, 传动更加平稳, 振动和冲击得以改善.

4 结语

通过对RV减速器一级行星传动轮系进行瞬态动力学分析, 得到完整周期下动态啮合等效应力图, 验证了轮齿交替啮合在周期内的规律, 并分别对输入轴齿轮和行星轮修形, 比较修形前后的传动性能, 得到了修形前后等效应力、速度曲线和加速度曲线, 结果表明在齿轮单、双齿交替啮合时刻, 存在速度、加速度波动, 伴随冲击振动. 由仿真数据可知, 修形后速度、加速度波动改善, 传动性能提高. 相关结果可以为RV减速器的设计、评估以及传动性能优化提供参考.

[1] 孟聪, 陈川, 杨玉虎. RV减速器模态特性分析[J]. 中国机械工程, 2018, 29(1):8-13.

[2] 彭鹏, 柯梁亮, 汪久根. 噪声干扰下的RV减速器故障诊断[J]. 机械工程学报, 2020, 56(1):30-36.

[3] 刘柏希, 王文军, 聂松辉. RV减速器扭转振动的固有特性及灵敏度分析[J]. 中国机械工程, 2016, 27(3):323- 327.

[4] Wang H, Shi Z Y, Yu B, et al. Transmission performance analysis of RV reducers influenced by profile modification and load[J]. Applied Sciences, 2019, 9(19):4099.

[5] 张大卫, 王刚, 黄田, 等. RV减速机动力学建模与结构参数分析[J]. 机械工程学报, 2001, 37(1):69-74.

[6] Wang C. Study on 3-D modification for reducing vibration of helical gear based on TCA technology, LTCA technology and system dynamics[J]. Mechanical Systems and Signal Processing, 2021, 146:106991.

[7] Li Q, Xie L Y. Analysis and optimization of tooth surface contact stress of gears with tooth profile deviations, meshing errors and lead crowning modifications based on finite element method and taguchi method[J]. Metals, 2020, 10(10):1370.

[8] Li T X, Tian M, Xu H, et al. Meshing contact analysis of cycloidal-pin gear in RV reducer considering the influence of manufacturing error[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2020, 42(3):1-14.

[9] Lin K S, Chan K Y, Lee J J. Kinematic error analysis and tolerance allocation of cycloidal gear reducers[J]. Mechanism and Machine Theory, 2018, 124:73-91.

[10] 濮良贵, 陈国定, 吴立言. 机械设计[M]. 9版. 北京: 高等教育出版社, 2013:198-201.

[11] Zhang Q Y, Wang Y R, Lin W P, et al. Dynamic performance of gear transmission system and modification optimization of electric vehicle gearbox[J]. Journal of Coastal Research, 2020, 103(S):366-372.

[12] 陈思雨, 唐进元, 王志伟, 等. 修形对齿轮系统动力学特性的影响规律[J]. 机械工程学报, 2014, 50(13):59- 65.

[13] 孙桓, 陈作模, 葛文杰. 机械原理[M]. 8版. 北京: 高等教育出版社, 2013:208-215.

Meshing performance analysis of gear modification transmission of RV reducer planetary gear train

WANG Jiayun1, LOU Junqiang1, LI Guoping1*, LUO Limin2, LI Chen2

( 1.Zhejiang Provincial Key Laboratory of Part Rolling Technology, Ningbo 315211, China; 2.Ningbo Zhongda Leader Intelligent Transmission Co., Ltd., Ningbo 315301, China )

In order to accurately identify the influence of tooth profile modification on the dynamic meshing performance and transmission performance of the planetary gear train of the RV reducer, an assembly model of the planetary gear train was established, and the transmission law of the input shaft gear and the planetary gear in dynamic meshing was analyzed by the finite element method. The maximum equivalent stress and minimum equivalent stress at the critical moment of meshing were found to be 14.47 MPa and 8.55 MPa, respectively. After comprehensive consideration, the tooth tip modification amount of the input shaft gear and that of the planetary gear were selected as the design parameters to be optimized. With dynamic meshing simulation analysis, the transmission performance was calculated after the tooth profile modification under the same load. The analysis results showed that when the gear teeth alternately mesh with single and double teeth, the speed and acceleration fluctuations of the gear reach the maximum, accompanied by shock vibration. After comparison and analysis, it was found that, with tooth profile modification, the speed and acceleration fluctuations were significantly reduced, and the transmission performance was significantly improved.

RV reducer; planetary gear; dynamic meshing; tooth profile modification; finite element method

TH132.46

A

1001-5132（2021）04-0049-06

2021−01−27.

宁波大学学报（理工版）网址: http://journallg.nbu.edu.cn/

宁波市“科技创新2025”重大专项（2018B10005, 2018B10007, 2019B10078）.

李国平（1967－）, 男, 湖北武穴人, 教授, 主要研究方向: 机械设计优化. E-mail: liguoping@nbu.edu.cn

（责任编辑 史小丽）