基于水动力性能的网箱网衣网目群化数值模拟方法研究
2021-07-07施兴华钱佶麒于泽群
施兴华,周 游,钱佶麒,于泽群
(江苏科技大学,船舶与海洋工程学院,江苏 镇江 212100)
网渔具和网箱是海洋渔业生产的重要工具和设施,网衣是其主要构件。与其他海洋结构物一样,网衣及其构成的渔具和渔业设施在海洋中要承受风、浪、流等水文环境因子的作用。网衣的水动力研究需要包含多个学科领域的交叉,包括数学、物理学、流体力学等,研究手段也非常的复杂[1-3]。
国内对于网箱和网衣的研究起步较晚。刘圣聪等[4]通过模型试验研究了周长40 m、网高10 m的HDPE圆形升降式网箱沉降在水下时的缆绳张力。胡克等[5]基于Abaqus二次开发技术,结合网平面经验公式,编写了水动力计算模型,验证了网箱在不同网格数和沉子质量时水动力和网箱体积计算结果的准确性,可以用来计算网箱在水流下的水动力。程晖等[6]为获得适合于深远海养殖的最优网箱结构,利用数值模拟方法,对投放于黄海冷水团的“钻石型”网箱箱体设计了5种结构方案,分析箱体结构的中部水平漂移、底部水平漂移以及网箱阻力等特性变化。崔勇等[7]基于有限元方法对波流共同作用下网箱的运动受力进行数值模拟,并将数值模拟结果与水槽模型试验结果进行比较分析,验证了程序及数学模型的可靠性。王绍敏等[8]采用有限元法,研究了网箱容积的变化趋势。
国外学者对网衣的研究相对较早。Trygve等[9]提出并讨论了网架上黏性水动力载荷的筛分式力模型,将数值计算结果与稳态圆网箱试验结果进行了比较,并讨论了数值计算结果对所选参数的敏感性。证明了阻力和升力随网的固度比和流速的变化规律是一致的。Lader等[10]将网衣假定为由非线性弹簧连接的微元网片组成的柔性体,采用数值方法对圆形网衣在水流作用下和平面网衣在单纯波浪作用下的受力及变形作了研究。
本研究提出了新的群化方案,保持了网目群化前后网衣的体积和质量不变,并通过调整水动力系数达到改进后的网衣所受水动力与未群化前相同。
1 网衣模型
1.1 运动方程
在本研究中基本的运动方程是在Brebbia等[11]的建议下在Morison方程的基础上进行修改的,公式如下:
(1)

(2)
1.2 网衣数值模型
在对网箱[13]进行数值模拟过程中,为简便计算,可将网箱的各个构件离散成许多有限长度的刚性杆件,集中质量法[14]则假设质量集中分布在这些杆件的中点或者端点处。本研究采用集中质量法,将网箱离散成无质量的杆件和杆件两个端点处的质点。对于网衣系统来讲,集中质量点即质点假设为网衣每个目脚的两端,每个端点的质量为四周所有相连的目脚质量的一半,如图1。
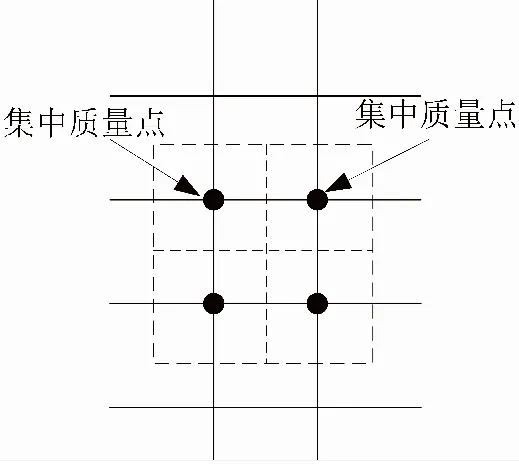
图1 网衣集中质量点示意图
通过计算集中质量点在水流和边界条件作用下的位移,来得到网衣变形后的形状。图2为网衣数值模型,结点标号:01,02。01-02表示一段网线。水流入射方向垂直于平面网衣,沿X轴正方向,X-O-Y平面位于水平面且Z轴正方向垂直于水平面向上。
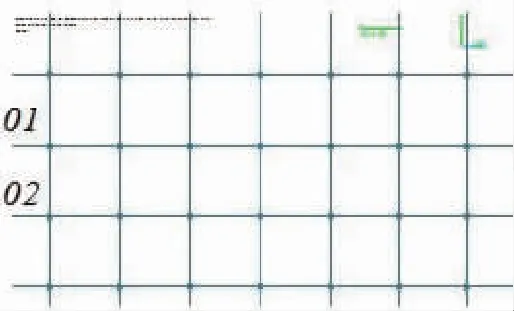
图2 网衣数值模型
2 网目群化改进方法分析
2.1 网目群化改进方法
网目群化方法在Lee等[16]和Bessonneau等[17]的文章都有提及,如图3所示。网目群化方法必须满足以下3个条件,原网片可以用群化后的网片代替:1)群化后网衣质量须和群化前网衣质量相等;2)群化后网目所覆盖的面积要和群化前相等;3)群化后网目沿流速方向的投影面积要和群化前相等。

图3 网目群化方式
对平面网片进行网目群化换算,根据以上3个条件进行验证的过程中发现,其模拟网目群化的效果并不理想。其主要原因是,同时满足以上3个条件,会导致网目群化后二者等效网线的体积大不相同,网目群化后体积增大,密度减小,于是最终导致了网衣体积增大,产生的浮力远远大于网目群化之前的浮力,致使数值模拟并不准确,如图4所示。

图4 网目群化前后网线的等效
所以为了网目群化方法能够继续进行并模拟准确,本研究在已有研究的基础上,提出了新的改进的群化方法。为了协调重力与浮力,改进方法保持了网目群化前后网衣的体积和质量不变,根据Morison方程调整水动力系数[18-21],从而达到改进后的网衣所受水动力与未群化前所受水动力相同。即
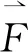
(3)
式中:CD1为网目群化前的速度力系数,CM1为网目群化前的惯性力系数,A1为网目群化前网衣沿流速方向的投影面积, m2;CD2为网目群化后的速度力系数,CM2为网目群化后的惯性力系数,A2为网目群化后网衣沿流速方向的投影面积, m2。
2.2 改进方法分析
平面网衣的宽度和高度分别为20 m和
12 m。密度为1 130 kg/m3,弹性模量为900 MPa,采用尼龙材料,目脚长度0.4 m,网线横截面直径为0.015 m。在网衣底部设置金属杆,抑制平面网衣在水流中的运动变形,金属杆长度为20 m,横截面直径0.04 m,密度为7 900 kg/m3,弹性模量为206 GPa。
网衣的水阻力系数切向力系数取为1.1,法向力系数取为0.1。底部金属杆由于完全浸没在水中,可以视为小尺度杆件,其水阻力系数与网衣相同。
对平面网衣分别进行3种方式建模[22-24],第1种无网目群化(M1),网目数量30×50,第2种将相邻的4个网目(2×2)群化为一个网格(M2),网目数量15×25,第3种将相邻的25个网目(5×5)群化为一个网格(M3),网目数量6×10。流速为0.4 m/s、0.8 m/s的纯水流,水流入射方向垂直于平面网衣,沿X轴正方向。图5为3种建模方式。
图6为平面网衣所受水平拖曳力的时历曲线。从图6中可看出,网衣在变形的初期阶段,其水平拖曳力迅速增加,随后在变形中期增速放缓,后期逐渐趋于稳定,网衣不再发生形变。当流速U=0.4 m/s时,大约在80 s左右,网衣达到稳态,而流速增加到U=0.8 m/s时,仅在40 s左右网衣就达到了稳态。当流速增加,其达到稳态所需的时间逐渐变少,网衣所受水平拖曳力也随之增加。
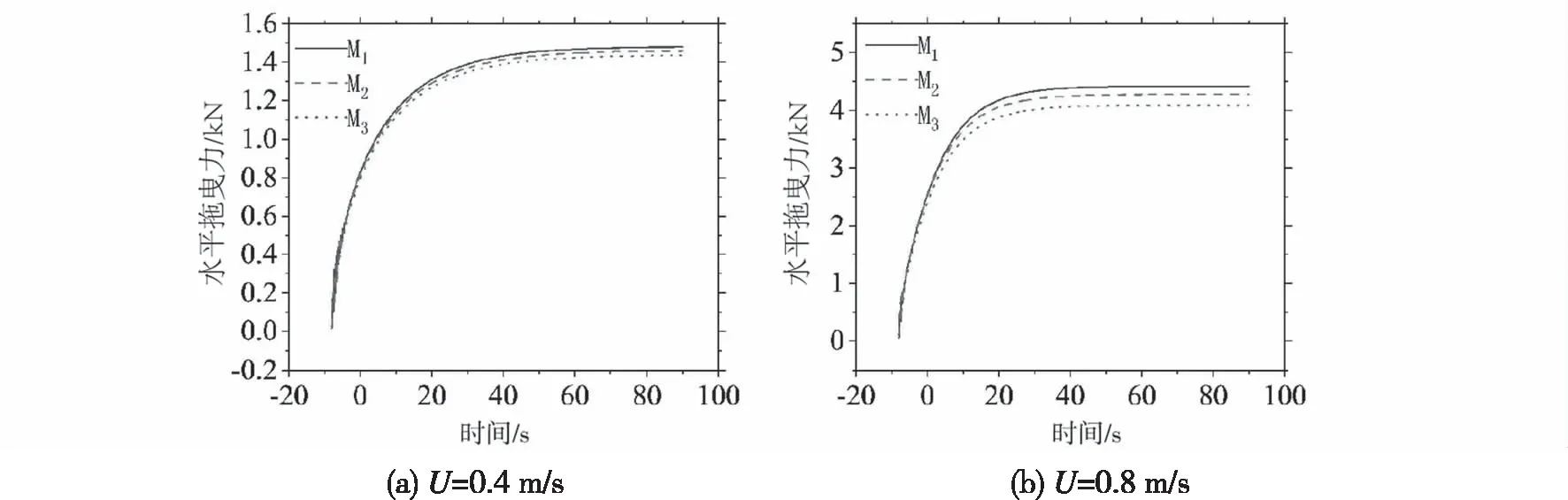
图6 平面网衣所受水平拖曳力
从图6可以计算出网衣所受水平拖曳力在两种网目群化方案下的相对误差。其中最大相对误差为M3,在流速为0.8 m/s时的7.51%,最小相对误差为M2在0.4 m/s时的1.4%。因此,本研究提出的网目群化方法在网衣的运动变形和网衣受力方面,其简化效果较好,满足精度要求。考虑到时间成本,网目群化后所需的时间远远小于未群化的模拟时间,节约了计算成本。
3 圆形网衣水动力学数值模拟
3.1 试验模型与数值模型
为了验证改进网目群化的准确性,与Lader等[25]的试验进行对比分析。试验网衣是由2块长125目、宽81目的矩形平面网片对接而成,材质为尼龙,正方形网目。圆形网衣[26-28]直径为1.435 m,高度为1.44 m。网衣固定在不锈钢圆环上,圆环固定不发生位移,其形变微小,可以忽略不计。圆形网衣网线目脚长度为16 mm,直径为1.8 mm,网线密度为1 130 kg/m3,弹性模量为350 MPa,泊松比为0.3。在网衣的底部布置了16个质量为400 g、600 g、800 g的沉子,从而达到控制网衣剧烈变形的目的。均匀水流流速分别为0.13 m/s、0.21 m/s、0.26 m/s、0.33 m/s、0.52 m/s。
采用本研究的方法将试验中的网衣进行网目群化,采用网目数量9×9的简化。直接将圆形网衣顶部固定,使其无法发生位移,从而达到与试验相同的模拟效果。并且由于本模型采用了网目群化的方法模拟,导致网衣底部的沉子无法与试验中的布置形式相同,在此模型中,将质量为16×400 g、16×600 g、16×800 g的沉子平均分成28份,
将其施加在网衣底部的28个结点上,使其达到相同的模拟效果。图7为试验模型和建立的数值模型。

图7 试验模型与数值模型
3.2 容积损失率
本研究采用Lader等[25]的结果分析中所提出的计算容积损失率的方法。各配重[29]模式下圆形网衣的容积损失率模拟值与试验值的对比如图8所示。在配重相同的工况下,流速与容积损失率基本成正比关系。根据已有的数值可推出在配重16×400 g的模型中,当流速约为U=0.59 m/s时,网衣的容积损失率将达到50%;在配重16×600 g的模型中,当流速约为U=0.89 m/s时,网衣容积损失率将达到50%;配重16×800 g的模型中,当流速约为U=0.89 m/s时,网衣容积损失率将达到50%。增加网衣底部配重可以有效减小网衣的变形,但是随着配重的增加,其变形抑制效果在逐渐降低。最大相对误差为11.21%,最小相对误差为0.42%,数值模拟结果与试验值吻合良好。

图8 容积损失率试验值和模拟值对比
3.3 网衣水平拖曳力
图9 为圆形网衣各配重下在不同流速时水平拖曳力时历曲线。圆形网衣在均匀流速的流场中,其水平拖曳力在初始阶段迅速增加,并且随着流速的增大,增加的速率也随之增大,随后达到稳态,数值基本不变。当配重16×400 g ,流速U=0.13、0.21、0.26、0.33、0.52 m/s时,分别在时间t为11.3 s、14.1 s、16.5 s、17.2 s、18.4 s时刻达到稳态;当配重16×600 g,流速U=0.13、0.21、0.26、0.33、0.52 m/s时,分别在模拟时间为5.4 s、9.6 s、12.5 s、14.2 s、20.9 s时刻达到稳态;在配重16×800 g 模型中,当流速U=0.13、0.21、0.26、0.33、0.52 m/s时,分别在模拟时间为1.2 s、7.0 s、9.5 s、12.1 s、12.1 s时刻达到稳态。可见在相同配重下,随着流速增加,其达到稳态所需的时间也在增加;而在相同流速下,达到稳态所需的时间随着配重增加而减少。

图9 圆形网衣受水平拖曳力时历曲线
各配重圆形网衣在不同流速时峰值水平拖曳力数值模拟与试验值比较如图10所示。在相同配重下,水平拖曳力随着流速增加而增大,两者呈线性关系。流速相同时,随着配重增加,稳态后的水平拖曳力有所增加。3种配重下,模拟值与试验值最小相对误差为0.8%,其他相对误差基本处于12%以下,数值模拟的结果与试验值吻合的较好。流速增大时,两者的误差增大,但都在计算误差允许的范围内。本研究与赵云鹏[30]的研究结果对比,其采用的未改进的网目群化方法相对误差在15%以内,可见改良效果有效。

图10 水平拖曳力峰值模拟值与试验值对比
4 结论
圆形网衣在均匀流速的流场中,其水平拖曳力随着流速的增大,速率也随之增大,随后达到稳态,数值基本不变。增加网衣底部配重可以有效减小网衣的变形,但是随着配重的增加,其变形抑制效果在逐渐降低。改进的网目群化方法可减少数值模拟时间,节约了计算成本,在水流作用下网衣变形和受力方面与试验结果吻合度良好。
□
