基于数字信号处理器的振动信号采集及边缘计算系统设计

2021-07-07刘海宁林心园李发家崔焕勇

济南大学学报（自然科学版） 2021年4期

刘旭，刘海宁，林心园，李发家，崔焕勇

(济南大学机械工程学院，山东济南 250022)

数据采集与处理是机械设备状态监测过程中的重要组成单元[1]。随着机械设备的大量应用以及人们对信号质量要求的提高，状态监测设备被大规模布置，采样频率也不断提高，使得获取到的振动数据呈指数级增长。海量数据不仅占据大量存储空间，占用大量带宽，阻塞网络，增加通讯成本，而且会占用服务端的计算资源，影响监测效率[2-4]。

为了解决状态监测中的大量冗余数据问题，郭俊锋等[4]提出一种双稀疏字典模型的压缩感知方法，在充分保留振动信息的情况下，实现了振动数据的有效压缩，减少了信号数据量。孙志伟等[5]提出一种系数分组编码与区间差分编码结合的压缩编码方法，在保留振动信号特征频率的同时，提高了信号的数据密度。Liu等[6]提出一种基于小波包变换、二维离散余弦变换(2D-DCT)以及符号聚合近似的子带编码技术，将采集的振动信号转变为机械状态哈希码，实现了数据信号密度的提升，并取得了良好的故障诊断和预测效果。

本文中结合TMS320F28335型数字信号处理器(DSP)、微机电系统(MEMS)加速度计、AD7606型模数转换(A/D)采样芯片、CH395L型以太网协议栈芯片，设计一种振动信号采集系统，并利用基于提升小波包变换(LWPT)、2D-DCT以及符号聚合近似(SAX)子带编码技术，完成边缘计算算法在DSP的快速实现，将振动信号在采集终端进行初步计算和处理，提高数据信息密度。

1 总体设计

振动信号采集系统的工作原理是在边缘端利用采集模块对振动信号进行采集，由DSP对信号进行LWPT、2D-DCT和SAX处理，最后通过通讯模块把处理结果上传至服务端，用于设备的进一步性能评估、故障预测和故障诊断。涉及的振动信号诊断流程如图1所示，其中虚线框内为本文中的振动信号处理流程。

系统的实现包括硬件和软件2个部分，如图2所示。硬件由MEMS加速度计及AD7606型A/D采样芯片构成的数据采集模块、TMS320F28335型DSP构成的数据处理模块和CH395L型以太网协议栈芯片构成的数据传输模块组成。软件主要完成系统初始化、数据类型转换、边缘计算和数据发送等程序设计。

LWPT—提升小波包变换；2D-DCT—二维离散余弦变换；SAX—符号聚合近似。图1 基于数字信号处理器的振动信号诊断流程

MEMS—微机电系统；TCP—传输控制协议；A/D—模数转换。图2 基于数字信号处理器的振动信号采集及边缘计算系统硬件框图

2 硬件设计

机械设备故障频率一般为十几赫兹至千赫兹，在设备状态监测过程中，通常需要多个通道实现多路振动信号的同步采集，因此需要选择较大频率带宽的传感器和每秒采样次数不少于1.5×104的多通道采样芯片。为了满足高效传输与监测的实时性要求，数据传输速度需大于1 Mb/s，并且传输距离大于200 m，因此，选用MEMS加速度计、AD7606型A/D采样芯片和CH395L型以太网协议栈芯片，完成系统的信号采集和数据传输工作。

系统采用TMS320F28335作为核心处理芯片，实现对系统的控制和数据的处理[7]。系统与其配套的接口电路主要分为2个部分：1)数据采集模块电路，包括MEMS加速度计的接口电路设计和AD7606型A/D采样芯片的接口电路设计；2)数据传输模块电路，即CH395L型以太网协议栈芯片接口电路设计，主要用于对边缘计算结果即机械状态哈希码的传输。

2.1 DSP

相较于单片机，DSP在实时性、可靠性、指令周期和执行速率等方面具有很大优势，更适用于需要处理大量信号的应用场景。TMS320F28335型DSP作为一款浮点型DSP，具有主频为150 MHz的高速处理能力，片内具有专门的硬件乘法器，在1个单指令周期中，芯片可以完成1次或2次乘法运算，大幅提高了运算速度[8-9]。采用哈佛结构，8级流水线可以并行处理多条指令，使用C语言实现复杂的数学算法，能够满足本系统振动信号快速处理的需求。

2.2 MEMS加速度计接口电路设计

与传统加速度传感器相比，MEMS加速度计不需要单独的恒流源供电，芯片制造成本更低，并且一致性好，易于批量生产，适合状态监测中的大规模布置。由于MEMS加速度计具有更高的集成度、更小的传感器尺寸和整体外形尺寸，因此能够靠近振动源放置，实现更可靠的测量。

Xout、STANDBY、ST、OR—引脚编号。图3 ADXL1005型微机电系统加速度计接口电路

2.3 A/D采样芯片接口电路设计

AD7606型A/D采样芯片为8通道16位同步采样A/D芯片，理论上，所有通道每秒同步采样次数均可达2×105，完全满足机械振动信号监测中的采样需求。配置引脚RANGE为高电平，可支持电压为±10 V的信号输入，由于AD7606型A/D采样芯片内部的信号调理电路中包含低噪声、高输入阻抗的信号调理电路，因此不再需要外部驱动[10]，AD7606型A/D采样芯片的8个引脚V1—V8可以直接与MEMS加速度计的输出Xout相连。短接CONVST_A和CONVST_B可同步接收DSP通用输入输出端口(GPIO)的信号，实现8通道同步采样。接口电路如图4所示。

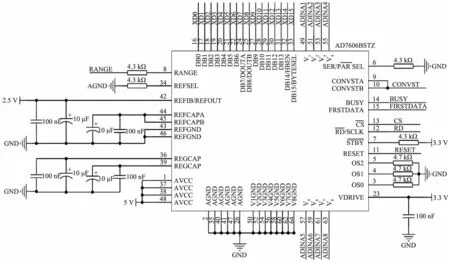
RANGE、V1—V8、CONVST_A、CONVST_B—引脚编号。图4 AD7606型模数转换(A/D)采样芯片接口电路

2.4 以太网协议栈芯片接口电路设计

以太网技术具有数据传输带宽大、系统稳定性好、传输距离远、实现成本低的优势。CH395L型以太网协议栈芯片自带10/100M(10～100 Mb/s自适应)以太网介质传输层和物理层，完全兼容IEEE 802.3协议，内置有传输控制协议/因特网互联(TCP/IP)协议栈。本文中在此基础上提出实现数据传输功能的以太网设计方案[11-12]。CH395L型以太网协议栈芯片分别与DSP和带网络变压器的信息插座连接器RJ45相连，其中，CH395L型以太网协议栈芯片与DSP串行外设接口(SPI)相连，使用频率为30 MHz的外部晶体振荡器，接口电路如图5所示。

图5 CH395L型以太网协议栈芯片接口电路

3 边缘计算方法

3.1 提升小波包变换

对于给定的信号X，提升小波变换[13-14]通过分裂、预测和更新将X分解为近似系数ai+1(i∈)和细节系数di+1，如图6所示。具体步骤如下：

X—给定信号；ai+1—近似系数，i∈；di+1—细节系数。图6 提升小波步骤

1)分裂。将给定序列X分裂为偶数样本序列ai,e和奇数样本序列ai,o,

(1)

式中n∈。

2)预测。构造预测算子P，用偶数样本序列ai,e预测奇数样本序列ai,o，误差为细节系数di+1，

di+1=ai,o-P(ai,e)。

(2)

3)更新。构造更新算子U，在细节系数di+1的基础上，对偶数样本序列ai,e进行更新，得到近似系数ai+1，

ai+1=ai,e+U(di+1)。

(3)

提升小波重构过程包含反预测、反更新和合并3个步骤，仅需对提升过程的逆变换调整正变换顺序、改变正负即可实现。提升小波包变换及其重构则是在提升小波方法和提升小波重构方法的多层运用。

3.2 二维离散余弦变换

通过行列分解技术，在行和列分别执行N个离散余弦变换后就能实现2D-DCT。Lee[15]提出了一种快速离散余弦变换算法，利用离散余弦变换的对称属性，将N个点的离散余弦变换转换成2个N/2个点的离散余弦变换，并不断分解和重复该过程，从而极大减少乘法的数量，主要计算步骤如下：

1)将序列x(n)分为g(n)和h(n)，

(4)

其中n=0,1,…,N/2-1。

2)进行2次N/2个点的离散余弦变换变换，得到离散余弦变换系数G(k)、H(k)为

(5)

其中k=0,1,…,N/2-1。

3)蝶形运算，

(6)

其中k=0,1,…,N/2-1。

3.3 符号聚合近似

1)标准化。标准化时间序列x为x′，使序列x′的平均值为0，标准差为1。

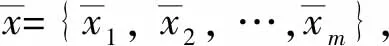
(7)

3.4 边缘计算算法

边缘计算算法流程如图7所示。首先，对采集得到的振动信号进行LWPT，得到提升小波包系数，然后对系数进行重构得到提升小波包重构系数；其次，对重构系数分组，得到分组矩阵，并将分组矩阵进行2D-DCT处理；再次，根据2D-DCT系数提取每组系数的特征值作为采集振动信号的子集特征值；最后，通过SAX将特征值转换为含有丰富机器状态信息的哈希码。

LWPT—提升小波包变换；2D-DCT—二维离散余弦变换；SAX—符号聚合近似；a1—第1层提升小波包近似系数；d1—第1层提升小波包细节系数；S1—S2j—提升小波包重构系数，j∈；分组后的系数；二维离散余弦变换系数；信号特征值，其中i,p∈。图7 基于LWPT、2D-DCT、SAX算法的边缘计算算法流程

4 软件设计

DSP程序采用C语言编程，系统软件运行中流程如图8所示。系统首先调用初始化程序，对DSP系统时钟、GPIO、SPI、外部接口(XINTF)、外设终端扩展模块(PIE)中断向量表进行初始化，然后关闭、清除中断标志，初始化AD7606型A/D采样芯片、CH395L型以太网协议栈芯片，DSP使能中断，从而启动AD7606型A/D采样芯片进行同步采样工作，并读取AD7606型A/D采样芯片数据寄存器中的数据转换结果，对采集到的一段振动信号数据编码转换，并进行提升小波包变换、离散余弦变换以及符号聚合近似计算。当数据转化完成时，启动CH395L型以太网协议栈芯片通过RJ45将数据发送到上位机，从而完成一次信号采集工作。

A/D—模数转换；LWPT—提升小波包变换；2D-DCT—二维离散余弦变换；SAX—符号聚合近似。图8 基于数字信号处理器的振动信号采集及边缘计算系统软件运行流程

5 实验分析

5.1 CL100型齿轮接触疲劳试验条件设置

在CL100型齿轮接触疲劳试验机上进行系统信号采集及处理结果的验证与分析，试验机与信号采集及边缘计算系统如图9所示。试验齿轮箱内主动轮齿数Z1=17，从动轮齿数Z2=19，支承轴承型号为HRB6406。设置试验机负载转矩为420 N·m，电机转速为1 480 r/min。

布置MEMS加速度计于试验齿轮箱主动轮支承轴承的正上方(见图9)，设置系统采样频率为20 kHz，在试验齿轮箱零部件正常状态(以下称为正常状态)以及齿轮箱常见的齿轮故障和轴承故障条件下分别进行试验，使用本系统采集相应振动信号。其中，齿轮故障设置为仅主动轮单齿点蚀(以下称为齿轮点蚀)，如图10所示。轴承故障设置为仅主动轮右侧支承轴承内圈点蚀(以下称为轴承点蚀)，如图11所示。

MEMS—微机电系统。图9 CL100型齿轮接触疲劳试验机与信号采集及边缘计算系统

(a)正常状态 (b)齿轮点蚀图10 试验齿轮箱主动轮的不同状态

图11 试验齿轮箱主动轮的支撑轴承点蚀故障

5.2 采集信号的有效性验证

系统结合MEMS加速度计分别采集并上传正常状态、齿轮点蚀和轴承点蚀的试验齿轮箱原始振动信号，时域图如图12所示。图13所示为正常状态和齿轮点蚀情况下振动信号的快速傅里叶变换(FFT)结果。从图13中可以看出，尽管齿轮的制造误差及安装误差造成了倍频幅值的增加，但是实际啮合频率f=468.75 Hz与理论啮合频率f0=468.67 Hz基本吻合。同时，系统使用传统加速度传感器进行原始振动信号采集，FFT结果与图13中的一致，由此验证了采集系统所采集振动信号的有效性。

(a)正常状态

f—齿轮实际啮合频率。图13 正常状态和齿轮点蚀振动信号的快速傅里叶变换结果

5.3 系统结果分析

在采集到的试验齿轮箱正常状态、齿轮点蚀和轴承点蚀的原始振动信号中，均选取100组数据，利用MATLAB软件，在PC端对每组1 024个点进行LWPT和2D-DCT计算，获取信号特征值，如图14(a)所示。进一步对特征值进行SAX处理，每组获得32个机械状态哈希码，结果如图14(b)所示。使用本系统对振动信号进行采集并对采集到的原始振动信号边缘计算处理，获得不同齿轮状态的哈希码，对比发现，本系统计算结果与图14(b)中的相同，验证了本系统边缘计算算法代码的准确性。

(a)特征值

通过边缘计算算法，1 024N个4字节浮点数的原始振动信号转换成仅由32N个2字节整型数字组成的机械状态哈希码，实现了原信号体积的64倍压缩。在机械设备状态监测中，这将大幅减小数据量，能够有效减少数据传输带宽占用，节约传输成本和存储空间，把初步计算放在网络边缘，能够节省服务端的计算资源。在图14(b)中，第1～100、101～200、201～300组分别为正常状态、轮齿点蚀、轴承点蚀情况下的哈希码，相同类型样本具有相同的特征，不同类型样本间哈希码存在明显差别，通过1组(32个)设备运行状态下的哈希码分别与1组正常状态、轮齿点蚀或轴承点蚀情况下的哈希码对比，能够判断机器的不同健康状态。由此可以得出结论：系统的边缘计算提高了数据密度，同时系统的计算结果可以表示机械设备的健康状态。