配筋增强钢管混凝土柱尺寸效应和承载力分析

阿里甫江·夏木西，阿依德尼古丽·都曼，谭 锬，史露江

(新疆大学 建筑工程学院， 新疆 乌鲁木齐 830046)

钢管混凝土(Concrete-filled Steel Tube，CFST)结构构件由于具备诸如高强度、可塑性和断裂韧性等卓越的力学特性，被广泛用于承受巨大荷载的高层、超高层、大跨度桥梁、工业厂房和地下结构中，与高强度混凝土配合使用更能得到较好的技术经济效益[1～3]。CFST填充物一般是混凝土，也有在混凝土内配置钢筋的情况，而这种通过配置钢筋增强后的CFST则称为配筋钢管混凝土(Reinforced Concrete-filled Steel Tube，R-CFST)[4～11]。经过几十年的研究，CFST的施工和设计经验现已成熟，2014年我国公布实施了GB 50936-2014《钢管混凝土规范》(以下简称CFST规范)[12]。相比之下，R-CFST表面上看虽与CFST类似，但由于其内配置钢筋的贡献其受力特性却发生较大改变[8]，其基本力学性能有待进一步探索。

实际工程中的圆形截面CFST或R-CFST由于承受巨大荷载其截面直径尺寸往往1 m以上，甚至有3 m以上的情况[1]，而实验室内的研究对象的直径大多在100～200 mm之间。因此，这些大型结构构件的安全性，特别是关于直径对钢管约束作用的影响，成为一个令人关注的问题。除此之外，目前已知的给出R-CFST承载力计算方法的规范有美国2010年公布的AISC[13]规范和我国2015年实施的CECS 408：2015《特殊钢管混凝土构件设计规程》(以下简称SCFST规程)[14]。美国规范采用叠加原理，根据既有研究[11,15]，其计算结果过分偏保守。我国SCFST规程在CFST规范给出的CFST短柱统一理论公式的基础上叠加纵筋强度的方法给出R-CFST承载力计算公式。从统一理论的基本思路看，将纵筋强度简单叠加显然不太合理而且有一定的不确定性，同时其结果偏保守较多[14]。

因此，本文通过轴心受压试验初步探索尺寸效应对R-CFST的强度、刚度退化、套箍效应等关键力学指标的影响，在试验研究基础上对R-CFST短柱的轴心受压承载力计算公式进行了研究。

1 试验方案

1.1 试件设计

本试验将尺寸效应作为研究对象，准备大尺寸和小尺寸两种类型的试件，各类型包括2根CFST(标识为CF)和2根R-CFST(标识为RF)试件。众所周知，套箍系数ζ是影响CFST受力形态的关键因素，我国CFST规范规定ζ的取值范围为0.5～2.0，可将ζ作为制备试件的主要参数，ζ的表达式为：

(1)

式中：Ags，Ac分别为钢管和混凝土的横截面面积；fgy，fc分别为钢管和混凝土的屈服强度和棱柱体强度。

根据本地区钢管供货情况，大、小尺寸试件的钢管直径分别为300,150 mm，壁厚均为3.2 mm，材质均为Q235B(暂取fgy=235 MPa)，先确定小尺寸试件的混凝土为C40(暂取fc=40 MPa)，由式(1)算出小尺寸试件的ζ值为0.8。保持大、小尺寸试件的ζ值相同，可确定大尺寸试件的混凝土为C20。大、小尺寸R-CFST试件纵筋数量分别为8根和6根，材质均为HRB335，规格均为6 mm，采用螺旋形箍筋，间距均为30 mm，环径均为100 mm，规格均为4 mm，材质均为冷拔钢丝。大、小尺寸试件高度分别为700 mm和450 mm。以上大、小尺寸R-CFST和CFST试件分别标识为RF300，RF150，CF300，CF150，各组重复试件数为2根。试件设计概况见图1。

图1 试件设计和应变片布局/mm

1.2 测量及加荷

在所有试件的纵、横向中心对称地布置四组纵、横向应变片，分别测量钢管纵向和环向变形。R-CFST试件的每根纵向钢筋上布置应变片用来测量其纵向变形。试件整体荷载和轴向位移由加载装置测得。钢管应变片布局示意于图1。

采用力控制加载模式，大尺寸试件速度控制为14～21 kN/s，小尺寸试件速度控制为3.5～5.3 kN/s。峰值荷载后钢管出现明显局部失稳即终止试验。试件安装照片如图2所示。

图2 试件安装照片

1.3 材质试验

图3 钢管和钢筋的材质试验结果

2 尺寸效应探讨

2.1 现象及破坏模式

R-CFST和CFST表现出相似的试验过程和破坏现象。当大、小尺寸试件承受的荷载分别达到2190，1050 kN时(钢管外侧纵向应变与材质试验钢管切片屈服应变接近)，试件的中部和端部开始出现钢管鼓起变形，随着荷载的继续增加，在试件端部首先出现局部失稳，之后向构件中部发展。继续增加荷载出现局部失稳的位置开始鼓曲，随后钢管表现出明显的褶皱和膨胀，试件告以破坏。最终破坏时试件端部尤其是上端加载顶板处发生严重变形。为了改善这种破坏，文献[7]采用在试件端部焊接钢板的方式，但仍然没有带来改善。

作为代表性情况，将RF300和RF150的内外破坏照片给出如图4所示。根据既有研究成果[18]，此类构件的破坏模式随ζ值的增加由剪切破坏向多腰鼓曲破坏形态转变。由图4可看出，本试验大尺寸试件表现出明显的剪切破坏面(如图4b中的斜向白色虚线)，是典型的剪切破坏形态。小尺寸试件则不出现剪切破坏面，而更接近多腰鼓曲破坏形态。说明尺寸效应对破坏模式产生影响。

图4 R-CFST试件的破坏形态

2.2 受力特性

本次试验获得的主要数据列于表1。为便于分析，将R-CFST和CFST各试件荷载和位移的平均值分别转变成平均应力和平均应变后，再将应力值除以最大值进行正则化，最后将其绘制成图5所示曲线。

表1 试验结果

(1)从图5可以看出，荷载达到峰值之前， 两种R-CFST显示出较为明显的差异，主要表现为RF150的刚度比RF300大，R-CFST对尺寸效应的反映较为敏感，而峰值荷载之后两种R-CFST的响应基本相同，对尺寸效应的反映降低。无论峰值荷载之前或之后，两种CFST表现出较为明显的差异。根据相关研究成果[19]，CFST中的约束效应还与径厚比(直径对钢管壁厚的比值)相关，径厚比越小约束效应越明显。本次试验中，RF300和CF300以及RF150和CF150试件的径厚比分别为93.6以及46.9，即小尺寸试件的径厚比明显偏小，这可能导致小尺寸试件的约束效应比大尺寸好，进而在峰值荷载前表现出更好的受力性能。另外值得注意的是：CFST和R-CFST相比对尺寸效应更敏感，可能的原因是配筋后核心混凝土的刚度和延性得到改善[8]进而降低尺寸效应对峰值荷载后受力性能的影响。

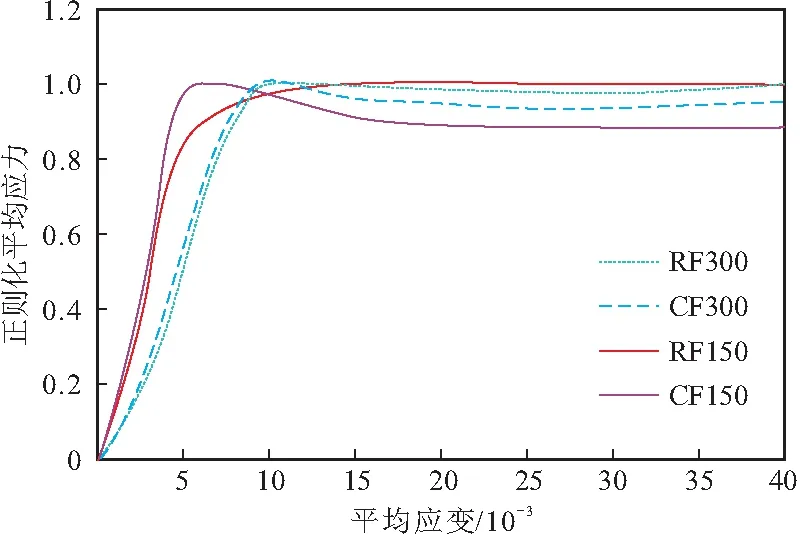
图5 正则化平均应力 - 应变曲线

(2)RF300和RF150峰值位移(对应于峰值荷载的位移值)平均值分别为7.58，7.35 mm，CF300和CF150峰值位移平均值分别为4.49，2.94 mm。可见，尺寸效应对R-CFST的塑性变形能力未造成显著影响，而对CFST塑性变形能力的影响较为明显。另外，R-CFST的位移值明显超过CFST，说明配置适量钢筋有助于提高塑性变形能力。

2.3 刚度退化

为讨论尺寸效应对峰值荷载后试件刚度的影响，计算了前述平均应力 - 应变曲线峰值荷载后每一数据点的割线模量，并对此割线模量进行正则化后得到如图6所示的刚度退化曲线。可以看出，R-CFST和CFST表现出相互类似的刚度退化趋势。其中，达到峰值荷载初期试件刚度退化迅速，RF300和RF150试件显示出基本相同的刚度退化趋势，随变形量的增加，刚度退化趋于平稳或缓慢，其中RF150试件的平稳趋势明显于RF300试件。另外，RF300试件表现出峰值荷载前的较大变形能力。除此之外，无论大尺寸还是小尺寸，CFST的刚度退化明显快于R-CFST。

图6 正则化割线刚度退化曲线

2.4 套箍指标

现行CFST规范[12]保留了2012年版《钢管混凝土规程》[20]基于套箍约束理论给出的圆形截面CFST承载力公式。该公式以ζ为参数，可以得出其计算式为：

(2)

式中：当混凝土立方体强度为55～80 MPa时k=1.8，其它情况取k=2.0；Nut取为各试件峰值荷载平均值。

由式(2)算出本试验各试件的套箍系数试验值并列于表1。所有试件设计时虽取了相同的套箍系数，但套箍系数的真实试验值各不相同。RF300和RF150的ζ试验值分别为1.46，1.66，后者比前者大13.7%，CF300和CF150的ζ试验值分别为1.25，1.42，后者比前者大13.6%。可见，尺寸效应对约束效应产生显著影响，尺寸小径厚比也就小，构件约束效应越明显，进一步验证了前文的结论。另外值得注意的是：无论大尺寸还是小尺寸，由于钢筋的贡献，R-CFST的约束效应明显优于CFST。

2.5 强度指标

Hasan[8]等人引入一强度因子来衡量R-CFST中的钢筋对承载力的贡献ηu，其表达式如下：

(3)

式中：Abs，fby分别为纵向钢筋的横截面面积和屈服强度。

本试验ηu的计算值给出于表1。RF300和RF150的ηu值分别为1.38，1.43，后者比前者大3.6%；CF300和CF150的ηu值分别为1.33和1.42，后者比前者大6.8%。可见，大尺寸试件的ηu值小于小尺寸，说明依据小尺寸试件的研究成果得出的强度计算公式应用于大尺寸构件的承载力计算得出的计算值偏小，结果偏于安全。

3 承载力计算公式

上述分析结果表明，尺寸效应对受力性能、破坏模式、刚度、套箍指标和强度等产生影响，其中对构件承载力的影响没有像约束效应那么明显，而且大尺寸的承载力计算结果偏于安全。由于钢筋的介入，CFST的承载力计算公式不完全适用于R-CFST。下面将讨论R-CFST的承载力计算方法。

3.1 SCFST规程公式

我国SCFST规程给出了R-CFST短柱轴压承载力计算公式，其表达式是在CFST规范[12]给出的CFST短柱统一理论公式[18]的基础上叠加纵筋的名义强度，即：

NR-CFST=NCFST+Nb

(4a)

(1)NCFST为CFST的统一强度，由CFST规范[12]给出的以下公式计算：

NCFST=Ascfsc

(4b)

fsc=(1.212+Bζ+Cζ2)fco

(4c)

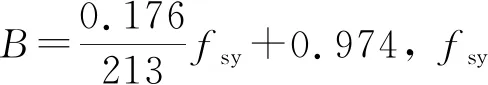
(2)Nb为纵向钢筋的轴心受压名义强度，按下式计算：

Nb=Absfby

(4d)

3.2 本文推荐公式

统一理论认为：CFST构件的受力性能，随着其材料特性、构件的几何和截面参数、截面应力状态的改变而改变，变化是连续的、相关的，而计算是统一的[18]。根据既有研究[4～11]，R-CFST中钢筋和核心混凝土较好地协同工作，较好地符合统一理论的基本假定。然而，SCFST规程给出的上述公式将纵筋的强度简单叠加，就不符合统一理论的基本观点，显得不太合理。

根据Hamidian等[9,11]的结论，R-CFST中的箍筋形式和间距不对承载力产生明显影响，而其纵向钢筋对套箍效应和承载力的贡献更为显著。另外，本试验还发现，R-CFST的承载力明显高于CFST的峰值荷载和纵向钢筋名义强度的叠加值(即NutR-CFST>NutCFST+Nb)，说明钢筋对强度的提高作用类似于钢管，可将其代替为钢管考虑在承载力计算中。因此，本研究认为R-CFST承载力计算不必考虑箍筋的二重套箍作用，而将承载力的提高归因于纵向钢筋，将其看作插入在核心混凝土的另一钢管。据此，定义R-CFST的套箍系数ζRF：

(5a)

现行CFST规范保留了基于套箍约束理论建立的CFST公式[20]，将上述R-CFST的套箍系数ζRF代入规范公式中，即可得出适合圆形截面R-CFST短柱的轴心受压承载力计算式为：

Nu=0.9Acfc(1+kζRF),ζ≤1/(k-1)2

(5b)

(5c)

诸多R-CFST相关文献中，文献[6]提供了包含对应CFST承载力信息的数据。分别用式(4)和(5)对本试验和文献[6]的R-CFST和CFST的实验数据进行了计算，并将数据给出在表2(表中Δ为差值)和图7中。

(1)CFST的承载力：CFST规范统一理论公式(式(4b))的计算结果普遍偏于保守(图7)，其中实验值对计算值的比值ΔCFST的平均值为1.34，标准偏差为0.17；ΔCFST最大可达1.54，对应的过高计算值达54.4%；

(2)R-CFST的承载力：SCFST规程(式(4))和本文推荐R-CFST公式(式(5))的计算值也同样偏安全(图7)， 其中两种公式Δ平均值分别为1.31和1.17，标准偏差分别为0.14和0.12，最大值分别为1.49和1.38。可见，本文推荐公式的计算值更加接近实测值、离散性更低、更准确地计算试件承载力。另外，本文推荐R-CFST公式和规范CFST公式的Δ值标准差分别为0.12和0.17，即前者比后者小，说明前者计算结果的离散性更低、结果更可靠。除此之外，本文提出的承载力公式的另一优势是它与我国基于统一理论的设计习惯匹配。

表2 实验和计算结果的对比分析

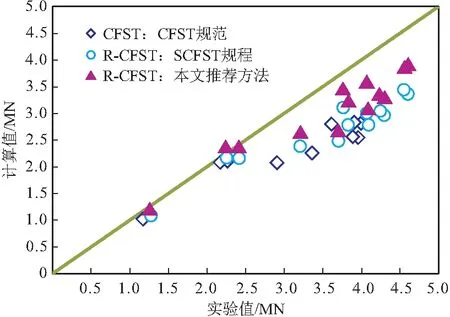
图7 R-CFST承载力计算方法比较

4 结 论

本文进行了两种不同尺寸R-CFST和CFST短柱的轴压试验，对大、小尺寸试件在破坏模式、受力、刚度、约束效应和承载力等方面的特性开展对比分析，初步明确了尺寸效应的影响。

(1)尺寸效应对破坏模式产生影响。破坏模式不仅与套箍系数有关，还与径厚比有关。钢管壁厚不变，构件尺寸越大径厚比越大，约束效应则越微弱，构件易于产生剪切破坏。

(2)最大荷载前，尺寸效应对R-CFST产生较大影响，最大荷载之后，R-CFST对尺寸效应的反映趋于降低。无论最大荷载之前或之后，CFST和R-CFST相比对尺寸效应更敏感。配筋后核心混凝土的刚度和塑性变形能力得到改善，进而降低尺寸效应对最大荷载后受力性能的影响。

(3)进入塑性变形阶段的初期，大、小尺寸试件显示出基本相同的刚度下降趋势，之后刚度退化趋于平稳，其中小尺寸更平稳于大尺寸。

(4)尺寸效应对约束效应产生显著影响。钢管壁厚不变，构件尺寸越大、径厚比越大，约束效应则越微弱。因此，设计此类构件时建议不仅将套箍指标作为参考值还应兼顾径厚比。另外，无论大尺寸还是小尺寸，由于钢筋的贡献，R-CFST的约束效应明显优于CFST。

(5)尺寸效应对承载力的影响没有像约束效应那么明显。R-CFST中，钢筋对承载力的贡献，随尺寸的增加而降低，因而依据小尺寸试件得出的强度计算公式应用于大尺寸构件算得的计算值是偏小的，结果偏于安全。

(6)R-CFST的承载力计算中，忽略箍筋的影响，而将承载力提高归因于纵向钢筋，将其看作插入在核心混凝土的另一钢管。这样修正的承载力计算公式与规范CFST公式一样偏于保守，结果更稳定、误差更小、更切合实际情况。