基于移动激光扫描技术的隧道断面变形检测方法*
2021-07-07叶龙杰
叶龙杰,张 卡,3,4,5
(1.南京师范大学 虚拟地理环境教育部重点实验室,江苏 南京 210023;2.南京师范大学 地理科学学院,江苏 南京 210023;3.江苏省地理信息资源开发与利用协同创新中心,江苏 南京 210023;4.江苏省地理环境演化国家重点实验室培育建设点,江苏 南京 210023;5.自然资源部城市国土资源监测与仿真重点实验室,深圳 518034)
变形监测是保证地铁隧道施工与运营维护的一项重大安全措施。传统的隧道变形监测方法(全站仪、断面仪等)效率和空间分辨率低,不能及时、全面地反映变形信息[1-2]。由于激光扫描技术的高精度、信息量大、抗干扰性强等特点,作为检测的新方法发展迅速,在隧道安全检测领域成为研究的热点[3-6]。国内外许多学者对此进行深入研究。Fekete等[7]详细总结了点云数据在隧道竣工监测中的应用方案。Gikas等[8]介绍了三维激光扫描仪在隧道施工中的应用方法,通过与传统方法的比较,分析了三维激光扫描技术在隧道监测领域的应用优势。李健等[9]运用基于点云法向量差异的点云分割算法对点云数据进行抽稀并构建地铁隧道模型,用以进行隧道整体变形分析。李珵等[10]提出了基于激光点云的隧道断面连续提取与形变分析方法,并对提取的两期断面进行了形变分析,有效的反映了隧道整体形变信息。杜黎明等[11]提出了基于移动激光扫描技术的一种迭代椭圆拟合去噪的方法,通过实测与理论断面进行对比分析了隧道的形变。现有方法[12-14]对断面变形都是用拟合法比较拟合偏差,或通过提取坐标差反映隧道形变,但是仅根据一维度的形变量进行分析,未考虑到隧道横断面变形归根结底是面积变化,不能全面定量描述形变信息。
针对当前研究方法的不足,本文基于移动激光扫描技术获取的按里程分布的相对坐标系下点云数据,如图1所示,提出了一种新的隧道断面变形检测方法。该方法根据隧道受外力情况下因形变引起的理论断面与实际测量断面之间的几何关系,提出基于多边形裁剪的拉伸度、挤压度形变指标检测方法,并利用实际的隧道点云进行验证。结果表明该方法可以精准地反映隧道在运营过程中受到外力作用的横、纵向变形。

图1 相对坐标系下隧道点云数据
1 研究方法
本文根据隧道因受外力作用而形变时引起实际断面相较于理论断面的位移,定义了一种新的隧道断面变形检测方法。总体的工作流程如图2所示。该方法首先通过对移动激光扫描车获取的隧道点云数据进行环片提取;然后,通过迭代椭圆去噪算法拟合隧道截面,以提升形变检测的精度;最后,利用改进多边形裁剪算法统计隧道环片的拉伸度、挤压度指标,综合环片各角度形变值检测隧道变形状况,并结合各角度形变值渲染图可视化形变信息。

图2 工作流程图
1.1 隧道壁噪声去除
在实际的隧道扫描过程中,由于受到障碍物的干扰以及狭小的隧道空间的限制,许多不属于隧道壁上的点云(支架、孔槽等),亦称之为噪声点,也被采集并记录下来。这些噪声点严重影响了后续隧道形变检测的过程,需要预先将其滤除,以得到属于隧道壁上的点云。根据盾构法施工隧道的形状结构多为离心率接近0的椭圆的特点,可以使用椭圆拟合的方法进行去噪。具体而言,本文首先使用RANSAC算法进行初始的椭圆拟合,计算出椭圆的中心点、长短半轴等几何参数;然后求算隧道横截面上所有点pi到椭圆的最短距离di,由其组成距离集合{di|i=1,2,…,n},由式(1)、(2)计算其均值dmean与标准差σ。
(1)
(2)
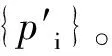
1.2 隧道形变分析
1.2.1 隧道角度形变计算
圆形盾构隧道的变形过程可以看作是由标准圆受地表力作用下成为椭圆的过程。因此,本文方法对隧道截面的形变分析是建立在1.1节中介绍的拟合椭圆基础上的,这样能够有效地提升计算效率及精度。如图3所示,令拟合椭圆的中心为坐标原点,且与设计标准圆的圆心重合。在此基础上,可以对隧道各角度上的形变值进行量测。具体而言,以椭圆的中心为原点建立局部截面坐标系XOY,作一条经过原点的角度直线,与拟合椭圆交于一点p(x,y),直线与X轴正向的夹角为θ。则在给定角度θ的交点到椭圆中心的距离d能够由式(3)计算:

图3 隧道角度形变计算示意图
(3)
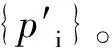
1.2.2 隧道形变性质统计
为了能够综合判断隧道形变的总体性质,定义了拉伸度以及挤压度两个测量指标来描述隧道受到的外力形变性质。具体而言,首先通过将隧道横截面以及施工设计的标准圆断面进行比较,采用多边形裁剪算法进行横断面形变面积统计,进而计算拉伸度与挤压度。
如图4所示,圆形轮廓线表示施工设计时的标准圆断面P1,椭圆形轮廓线表示隧道横截面P2。由于受到外力作用,图中红色区域表示隧道环片受外力产生的拉伸区域P2-P1;蓝色区域为隧道环片受外力产生的挤压区域P1-P2。由式(4)、(5)计算隧道拉伸度S以及挤压度E。拉伸度越大表示隧道环片拉伸形变越大,挤压度越大表示隧道环片挤压形变越大。

图4 隧道断面不同时期的形变量
(4)
(5)
本文使用改进的基于错切裁剪的多边形裁剪算法来求取挤压区域P1-P2以及拉伸区域P2-P1。与原算法相比,该方法采用参数方程而不是斜截式表示直线,利用参数方程求交取代原方法利用错切变换求交点,从而避免较高的计算复杂度操作。一般而言,任意多边形的裁剪可以分解为多个线裁剪。根据线裁剪定义,假设裁剪边L1两端点为Va(xa,ya)、Vb(xb,yb),被裁剪多边形的某一边L2两端点为Vj(xj,yj)、Vk(xk,yk),则L1、L2可以由参数m与n分别表示为:
(6)
由于进行多边形裁剪时,需要计算L1、L2的交点。当两边相交即有共同点时,联立解方程:
(7)
可以得到L1、L2的参数值,如式(8)所示。
(8)
当L1、L2两直线段有交点时,求得参数满足m,n∈[0,1],否则,L1、L2没有交点。当一条边有多个交点时,需要按照每个交点对应的参数值m和n的大小顺序,对这些交点进行排序。
由计算出的交点,标识出该点属于裁剪多边形的线段进入或离开被裁剪多边形的状态,简记为进点、出点。将其插入裁剪多边形和被裁剪多边形构成循环单链表,通过遍历被裁剪多边形搜寻进点、出点,输出结果多边形。最后,根据裁剪结果获得挤压区域亦即拉伸区域。进而由式(9)计算拉伸面积P2-P1与挤压面积P1-P2:
(9)
式中,Ω为多边形面积;(xi,yi)为多边形顶点集合{Vi|i=1, 2,…,N}的坐标值,N为多边形顶点个数。
2 实验与分析
2.1 实验数据
为了验证本文方法的有效性,用C++语言在主频为2.5 GHz的微机上实现了该方法与基于错切裁剪多边形裁剪算法[15],并用两种测量方式获取的点云数据进行对比实验。实验采用CNU-TS-1隧道检测小车[16]进行二维相对移动激光扫描,逐里程获取密集断面点云数据,如图5所示。

图5 移动激光扫描数据获取场景
用上述设备获取成都某地铁圆形盾构隧道竣工后的激光扫描点云数据。该区段隧道由混凝土构成,总长度为100 m,坡度为0°即走向水平。点间距小于2 cm,扫描精度为2 mm,共获取到5 000 000个点。该圆形盾构隧道是由实际直径为5.4 m、长度为1.5 m的环片拼接而成。实验选择了其中31个环片的数据作为实验样本,将圆形环片直径作为基准进行隧道断面分析,如图6所示。

图6 俯视角度隧道环片示意图
2.2 实验结果
2.2.1 隧道横截面点集采样
采集到的隧道激光点云数据包含了31个环片,并且每一个环片包含1.5 m里程的横截面点云,显然对所有的数据进行形变分析是不实际的。因此,需要对每个环片进行采样,选择位于每个环片中心的横截面点云作为样本,进行该隧道环片的形变分析。如图7所示,试验根据移动车载扫描车的扫面线提取到了31个横截面点云。值得注意的是,每个横截面点云属于同一平面(同一扫描线)。

图7 成都地区点云隧道环片横截面点云提取结果
2.2.2 隧道横截面点云去噪
由于隧道环片上有支架、孔槽等不属于隧道环片的其它结构,这些结构对于隧道形变检测是无意义的[17],进行迭代椭圆拟合去噪后,可以得到属于隧道环片上的测量点云。经过10次迭代椭圆拟合去噪后,结果如图8所示。图8中红色矩形框展示了噪点去除效果。结果表明,所述方法能够有效提取隧道横截面点云,与此同时,隧道壁上的激光点云能够被有效保留。

图8 横截面点云数据
2.2.3 隧道角度形变计算
本次实验区中的隧道采用内径为5.4 m的环片拼接而成,将其视作隧道壁的初始直径基准值。将理论半径(2.7 m)与拟合出的31个椭圆断面线的0°以及90°方向的长、短半轴进行比较作差,可以得到各环片的横向、纵向变形值。1~31环片的横向、纵向变形值曲线如图9所示。可以看出,其横向变形值在区间[0 mm,+12 mm]内,最大变形值发生在第23环片。而纵向变形值位于[-26 mm,0 mm]。总体来说,位于90°方向的椭圆短半轴小于理论半径,表示环片受到挤压收缩;而0°方向的椭圆长半轴则大于理论半径,表明发生了拉伸变形。
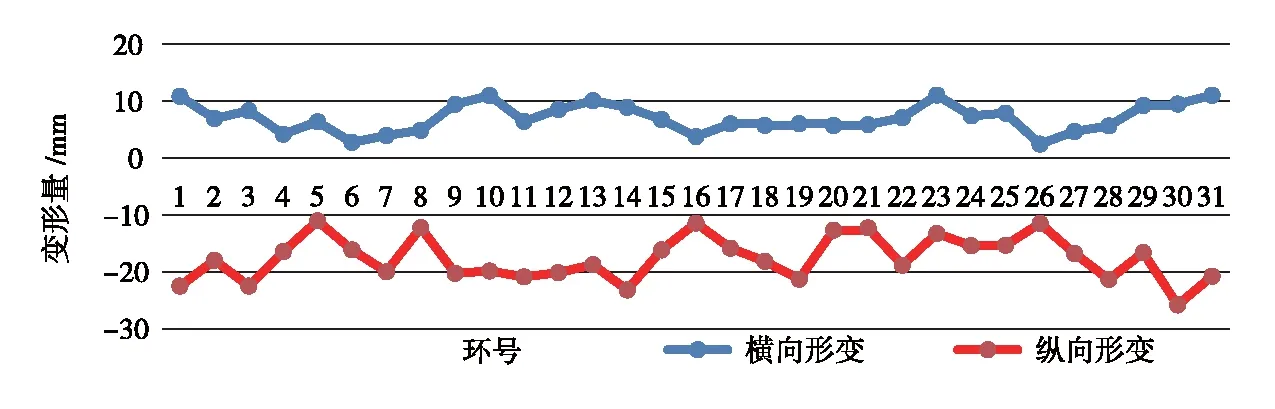
图9 隧道各环片的形变值
2.2.4 环片拉伸度与挤压度统计
通过计算1~31号环片的拉伸度统计值,可以发现它们位于0.033%~0.246%之间,且拉伸度最大的椭圆位于23号环片。隧道各环号拉伸度统计曲线如图10所示。与之相比,隧道的挤压度则反映了隧道顶部的形变状况。隧道挤压度的最大值为0.766%,位于第30号环片处,表明该环片顶部受到的挤压力最大。挤压度曲线如图11所示。

图10 隧道各环号拉伸度统计

图11 隧道各环号挤压度统计
2.2.5 形变信息可视化结果
如1.2.1节所述,根据各个激光点与X轴方向的夹角,可以计算得到每个点位上的变形值。导入CloudCompare软件中进行可视化显示,且点云按照变形值进行渲染。总体而言,点云变形值范围在[-25 mm,+15 mm]区间内。在视觉上,隧道壁上变形值大于10 mm呈现出红色,而变形值小于-10 mm则显示为蓝色。变形值处于[-10 mm,+10 mm]区间内显示为浅绿到黄色,表示该部分形变在正常范围内。环片1~9的形变信息可视化结果如图12所示,可以发现隧道环片顶部较容易受到挤压,而两侧隧道壁则发生了拉伸形变。

图12 隧道形变值俯视图(上)、侧视图(中)、正视图(下)
为了对比本文算法与基于错切裁剪多边形算法的时间效率,本文随机给出N个顶点的两个多边形,并统计两算法对它们做裁剪操作所需的时间,结果如表1所示。由表1可知,随着顶点数增加,本文算法效率将显著高于基于错切裁剪的多边形裁剪算法。由此看出,改进算法确实减少了求交点过程的计算复杂度。
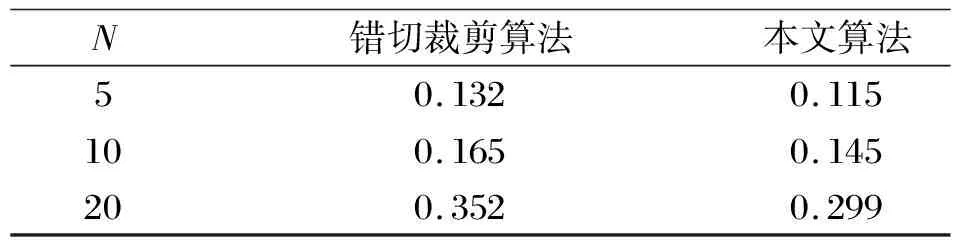
表1 本文算法与错切裁剪算法执行10 000次裁剪时间比较/s
2.3 分析与讨论
通过实验结果可以得出:隧道在变形监测期间,成都隧道环片由设计时的标准圆结构,因为受到地表建筑物的重力作用,使得顶部受到挤压,整体隧道断面结构变形为椭圆形,隧道顶部环片受力发生纵向挤压形变,而两侧环片发生了横向拉伸形变。由此可见,利用本文提出的挤压度以及拉伸度指标可以快速定位出形变较大的环片,为维护隧道安全提供有力的保障。按照形变值渲染后,能够直观地检测环片的各方向变形值从而反映隧道形变情况。
另外,文中所述算法在求交的时间复杂度O(n2)不变的情况下,能够防止退化,拥有更强的鲁棒性。以上分析说明,改进多边形算法适用于隧道形变检测,其检测效率满足一般工程需求,相对于基于错切裁剪的算法具有更强的泛化能力,面对断面线局部斜率无穷大时,依然能够进行有效地计算。
3 结 论
本文提出了基于移动激光扫描技术的隧道断面构建与断面叠加变形分析方法。相对于现有的断面检测方法,本文根据隧道受外力情况下因形变引起的原始隧道环片断面与实际测量断面间的几何关系,提出结合基于多边形裁剪的拉伸度、挤压度形变指标检测方法。由于数据采集的时间限制,实验中取而代之使用半径2.7 m圆形的管道环片作为隧道首次断面测量,在工程测量中是符合要求的,因为环片过大过小将不能进行安装。通过对比分析,本文算法比基于错切裁剪的多边形裁剪算法的效率更高,证明了本文算法的可行性和有效性。使用成都地区隧道点云数据进行实验,结果表明本文方法能够更直观地反映隧道形变信息,研究成果可为隧道形变动态监测提供借鉴。
