基于双卡尔曼滤波的梯次利用电池SOP估算研究

2021-07-06柴建勇侯恩广李岳炀

电源技术 2021年6期

柴建勇，侯恩广，李岳炀

(1.山东高速信息集团有限公司，山东济南 250101；2.山东交通学院，山东济南 250357；3.济南大学，山东济南 250022)

近几年，随着退役电池的数量增大，动力电池的梯次利用越来越受到人们关注。由于梯次电池性能退化、容量衰减，其安全性难以保障，导致梯次电池难以大规模推广利用。电池峰值功率状态(SOP)作为电池安全控制及能量回收的重要参数，越来越受到研究者的关注。常用的SOP估算方法有电池实验法和模型法。电池实验法是美国先进电池联合会(USABC)采用的测试方法[1]，具有可实施性强等优点[2]。中南大学李方[3]以及哈尔滨理工大学胡宇[4]采用了实验法。实验法无法改变测试繁琐、对设备要求高的缺点。于是，基于等效电路模型估算方法得到了更多的运用。最早提出基于等效电路模型估算峰值功率方法的是Plett G L[5]。文献[6-7]采用一阶等效电路模型，进行了SOP的估算。模型法[8-10]对电池等效模型依赖较大，进一步提高电池等效模型的准确性是研究电池SOP的重要方向之一。针对梯次电池性能退化导致电池峰值功率(SOP)估算偏差较大，首先建立梯次电池的二阶Thevenin 等效模型，其次应用双卡尔曼滤波算法，基于该算法估算SOC(荷电状态)、欧姆内阻和实际容量；然后利用最优估计预测工作电压与内阻，估算梯次电池SOP；最后建立梯次电池SOP的估算方法，为梯次电池的推广利用提供安全保障。

1 梯次电池二阶Thevenin等效模型

本文采用二阶Thevenin 模型为电池等效模型，等效电路图见图1。

图1 二阶Thevenin模型等效电路图

由图1 可知，梯次电池等效电路的离散状态方程：

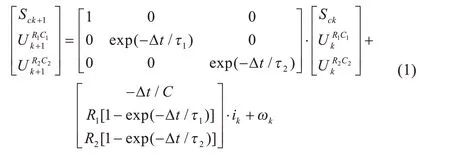
由图1 可知，梯次电池等效电路的离散观测方程：

式中：Sck、Sck+1分别为离散状态k、k+1 时刻梯次电池的SOC值；C为梯次电池实际容量，Ah；ik为离散状态k时刻的充放电电流；Uk为离散状态k时刻梯次电池的工作电压；Δt为采样周期；τ1=R1C1为R1、C1环节的时间常数；τ2=R2C2为R2、C2环节的时间常数；分别为离散状态k、k+1 时刻R1的电压估算值；分别为离散状态k、k+1 时刻R2上的电压估算值；ωk、υk为互不相关的系统噪声；η 为库仑系数；UOC(Sc)为离散状态k时刻梯次电池SOC值对应的电池开路电压。

2 梯次电池SOP 估算

本文中，在二阶Thevenin 等效模型基础上，应用双卡尔曼滤波算法：一是基于卡尔曼滤波算法估算SOC；二是基于卡尔曼滤波算法估算欧姆内阻和实际容量。

2.1 基于卡尔曼滤波算法估算梯次电池SOC

由式(3)、(4)可知，梯次电池系统的变量为SOC。由于梯次电池欧姆内阻和实际容量退化严重的问题，本文将梯次电池欧姆内阻和实际容量加入到状态变量中，系统状态变量共有三个参数：SOC、欧姆内阻、实际容量。

首先对状态方程和观测方程进行扩维：

状态方程：

观测方程：

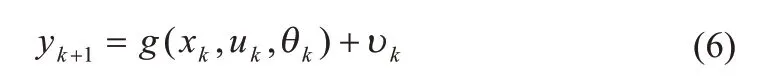
式中：θk表示的是状态变量欧姆内阻和实际容量,xk为系统状态变量；uk为系统的输入，即梯次电池电流；yk为系统观测变量，即梯次电池工作电压。扩维后的SOC估计，作为dual EKF 中的一个估计过程。

2.2 基于卡尔曼滤波算法估算梯次电池欧姆内阻和实际容量

新加状态参数的系统状态方程为：

式中：γk为噪声扰动。

新加状态参数的观测方程为：

式中：ek为输出变量上的噪声干扰。对状态变量θ 应用扩展卡尔曼滤波算法，得到电池内阻和额定容量的实时估计结果。为了得到精确的电池欧姆内阻和额定容量，采用观测变量梯次电池工作估算值和实际值的误差进行修正。这样状态变量θ 的状态空间模型，形成dual EKF 中的另一个估计过程。

2.3 梯次电池SOP 估算流程

本文中，零均值高斯白噪声ωk、υk、γk、ek的误差协方差矩阵分别为

Dual EKF 算法流程:

(1)初始化x：

(2)初始化θ：

(3)系统状态x的时间更新：

(4)系统状态θ 的时间更新：

(5)系统状态x的状态更新：

卡尔曼增益计算：

状态变量最优估计：

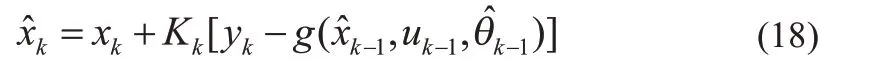
协方差最优估计：

(6)系统状态θ 的状态更新：

卡尔曼增益计算：

状态变量最优估计：

协方差最优估计：

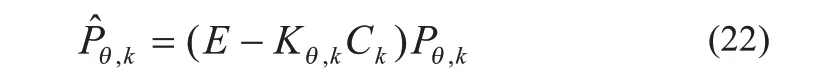
(7)SOP最优估算预测更新：

k+1 时刻最优估计预测工作电压：

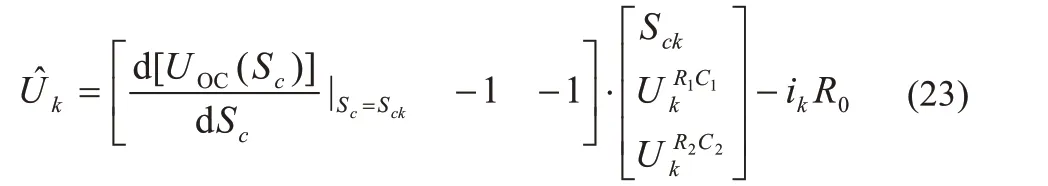
k+1 时刻最优的工作估计SOP：

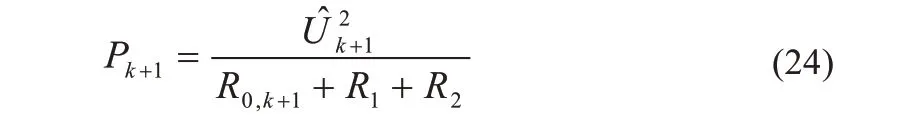
忽略极化内阻的影响，即：

式中：yk为采样k时刻的实际工作电压观测值；为采样k时刻观测变量的估算值；分别为采样k时刻系统状态x、θ 的误差协方差最优估算值；Pk、Pθ，k分别为采样k时刻系统状态x、θ 的误差协方差估算值。

2.4 梯次电池SOP 估算流程图

梯次电池SOP估算流程图，如图2 所示。

图2 SOP估算流程图

3 仿真验证

实验方法：选取18650 三元梯次电池，在室温环境下，应用德普BTS20-5V/4*300 A/WD 单体电池充放电设备，进行放电实验；对充满电的梯次电池进行放电，分10 次放电完成，模拟简单的工况，每次放出梯次电池容量的10%，每次采用不同放电电流，验证等效模型的准确性和SOP估算的准确性。

由上述公式和流程图可知，梯次电池的SOC估算精度是其中一个卡尔曼滤波算法的重要表征参数；梯次电池的工作电压估算精度是双卡尔曼滤波算法的重要表征参数；本文对梯次电池的SOC曲线、工作电压曲线和SOP曲线进行分析，验证算法的准确性。

图3 和图4 为梯次电池SOC仿真验证曲线图。其中，图3为梯次电池荷电状态SOC曲线图，图4 为梯次电池荷电状态SOC实际值与估算值的误差曲线。通过图3 曲线对比和图4误差分析，梯次电池SOC估算误差在1%以内，精度较高，为SOP估算提供了必要条件。

图3 梯次电池荷电状态SOC曲线

图4 梯次电池荷电状态SOC误差曲线

图5 和图6 为梯次电池工作电压仿真验证曲线图。其中，图5 为梯次电池工作电压曲线图，图6 为梯次电池工作电压实际值与估算值的误差曲线。通过图5 曲线对比和图6 误差分析，梯次电池工作电压实际值和估算值最大差值在20 mV 以内，梯次电池工作电压平台为3.7 V，计算的误差在1%以内，精度较高，为SOP估算提供了必要条件。

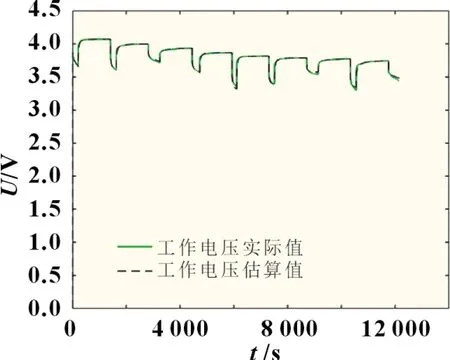
图5 梯次电池工作电压曲线

图6 梯次电池工作电压误差曲线

图7 和图8 为梯次电池峰值功率SOP仿真验证曲线图。其中，图7 为梯次电池峰值功率SOP曲线图，图8 为梯次电池峰值功率SOP实际值与估算值的误差曲线。通过图7 曲线对比和图8 误差分析，梯次电池峰值功率SOP实际值和估算值最大差值在2 W 以内，梯次电池额定功率为13.69 W，计算的误差在1.5%以内，精度较高。