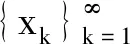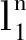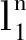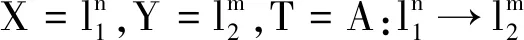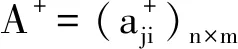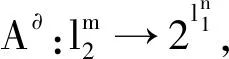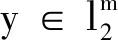非完全有限维金融市场未定权益定价的度量广义逆方法*
2021-07-06王筱凌王玉文
王筱凌,王玉文
(1. 黑龙江财经学院;2.哈尔滨师范大学)
0 引言



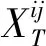

(2)
其中上标“T”为矩阵的转置.
1 可达权益的套利定价的已知结论

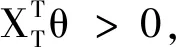


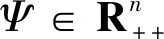
如果m个向量{θ(i)∈Rn}1≤i≤m满足
(4)
则称{θ(i)}1≤i≤m为Arrow-Debreu证券.t= 0时刻,投资组合θ(i)的价值为
即Arrow-Dedreu证券θ(i)在t=0时刻的价格为ψi(i=1,2,…,m).
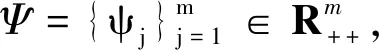
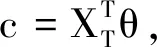
记

则对于任意投资组合θ∈Rn,有
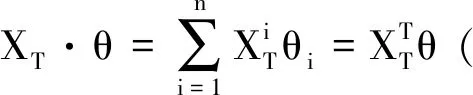
因此,由定义1.1,c∈Rm可达,当且仅当,存在θ∈Rn满足c=XT·θ,于是得到
于是可知,如果市场无套利,则对任意可达的权益c,其在t= 0时的价格为
c0=e-rTEQ[c]=e-rTEQ[XT·θ]=X0·θ
(6)
定义1.2 金融市场称为完全的,如果对每一个未定权益是可达的,即
∀c∈Rn,∃θ∈Rn,使得:c=XT·θ
引理1.1[2]一个由n个可交易资产组成的,按照从t= 0 时刻到t=T时刻模型演变的市场,如果在这段时期[0,T]内,经过N个交易日,在T时刻,每个可交易资产的价值,对应于m个状态之一,那么这个市场是完全的当且仅当n大于或等于m,且偿付矩阵的秩为m.
证明(参见文献[2]命题1.6.5)
因此,在现实中,完全金融市场只是理想情形,应该讨论非完全金融市场中定价.
2 非完全金融市场中未定权益的定价
以下假定m>n,因此金融市场是非完全的.为讨论方便,令

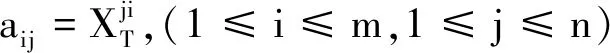
当m>n时,金融市场非完全.设矩阵A的秩为n,此时A的值域为n维子空间,且
R(A)={Ax:x∈Rn} ⊂Rm
在空间Rm中赋l2范数,即对y∈Rm,定义


设A=(aij)1≤i≤m1≤j≤n,对于x=(x1,x2,…,xn)T∈Rn,定义y=(y1,y2,…,ym)T=Ax
(8)
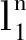
证明(参见文献[3]).
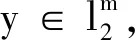
y=PP(A)(y)+y1,,y1∈R(A)┐

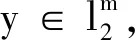
如果x0∈A-1PR(A)(y),即Ax0=PR(A)(y),则称x0为Ax=y的最小二乘解;
如果x0∈A-1PR(A)(y),且对任意x∈A-1PR(A)(y),有‖x0‖2≤‖x‖2,则称x0为Ax=y的最小l2范数最小二乘解,亦称最佳逼近解.
如果x0∈A-1PR(A)(y),且对任意x∈A-1=PR(A)(y),有‖x0‖1≤‖x‖1,则称x0为Ax=y的最小l1范数最小二乘解,也称最佳逼近解.
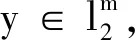
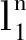
设{xn}⊂A-1PR(A)(y),x0∈Rn满足‖xn-x0‖1→0(n→∞),由定理2.1,有
‖PR(A)(y)-Ax0‖2=‖Axn-Ax0‖2≤‖A‖‖xn-x0‖1→0


(9)
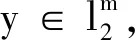
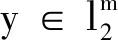
0 选正整数k>0,满足 使得 inf {‖x‖1:x∈A-1PR(A)(y)}- 满足‖xl-x0‖1→0,(l→∞). 由引理2.2,知x0∈A-1PR(A)(y). 且由范数的连续性,有‖x0‖1=inf{‖x‖1:x∈A-1PR(A)(y)},故由A∂(y)的定义,知x0∈A∂(y),即A∂(y)非空. 任取x1,x2∈A∂(y),由引理2.2及A∂(y)的定义,有 λx1+(1-λ)x2∈A-1PR(A)(y) , 且‖λx1+(1-λ)x2‖1≤λ‖x1‖1+(1-λ)‖x2‖1=inf{‖x‖1:x∈A-1PR(A)(y)} 于是λx1+(1-λ)x2∈A∂(y),所以A∂(y)为凸集. xk∈A-1PR(A)(y),‖xk‖1=inf{‖x‖1: x∈A-1PR(A)(y)},(k=1,2,…);x0∈A-1PR(A)(y), 定义2.2[4]设X,Y为Banach空间,T∈L(X,Y)为线性算子,集值映射T∂:Y→2D(T)定义为 T∂(y)={x0∈D(T):x0为Tx=y的最佳逼近解},y∈D(T∂) (10) 称为T的集值度量广义逆,其中 D(T∂∈)={y∈Y;Tx=y在D(T)中有最佳逼近解} (11) 此处,x0∈D(T)称为Tx=y的最佳逼近解,是指: Tx0-y‖Y=inf{‖Tx-y‖Y:x∈D(T)}, 且对任何满足 x1∈D(T),‖Tx1-y‖Y=inf{‖Tx-y‖Y:x∈D(T)} 的x1,有‖x0‖X≤‖x1‖X. 如果单值算子Tσ:D(T∂)→D(T)满足: ∀y∈D(T∂),Tσ(y)∈T∂(y),则称Tσ为T∂的单值选择. 1974年,Nashed M Z与 Votruba G V在文献[4]中提出研究建议:集值度量广义逆具有良好性质的单值选择是值得研究的.这一研究建议,自2008年文献[5]的研究之后得到实质进展.该文研究此建议的具体案例. (1)AA+A=A; (2)A+AA+=A+ (3)(A+A)*=A+A; (4)(AA+)=AA+ 则称A+为A的Moore-Penrose逆. 引理2.4[7]设A=(aij)m×n为m×n阶实矩阵,则 (1)存在A的唯一Moore-Penrose逆A+: 证明(参见文献[7]). (12) (13) 证明(1)由引理2.1可得. (2)由引理2.3可得. ‖x0‖2=inf{‖x‖2:x∈A-1PR(T)(y)} (14) (15) 由于 ∀x∈Rn,有‖x‖2≤‖x‖1,从而由(15)及A∂(y)的定义,有 (16) 另一方面,由(14)知,唯一的x0∈Rn,满足 ‖x0‖2=inf{‖x‖2:x∈A-1PR(T)(y)}≤inf{‖x‖1:A-1PR(A)(y)} (17) 下面讨论上述结果在证券定价中应用. ‖y-PR(T)(y)‖2=inf{‖y-z‖2:z∈R(T)} (18) C0=e-rTEQ[PR(A)(y)] (19) 于是由(6),(18)及(19)式,有 C0=e-rTEQ[XT·x]=X0·x=X0·A+y