捷联惯性基组合导航鲁棒UKF方法

张梦得，胡柏青，赵仁杰，田佳玉

(海军工程大学 导航工程教研室，湖北 武汉 430033)

0 引 言

组合导航系统是将2 种或者2 种以上的非相似导航系统的输出进行综合处理,获得更高的导航精度与可靠性[1-2]。最常见的组合导航系统是以惯导为核心的惯性基组合导航系统[3-4]。捷联惯导（Strapdown Inertial Navigation，SINS）具有用数字平台代替实体平台，结构简单，体积小，重量轻等特点，成为研究的热门[5]。然而SINS 却存在导航精度随时间发散的问题，无法仅仅依靠自身校正误差[6]。这就是SINS 需要与其他导航设备进行组合导航的原因，常见的基于捷联惯导的组合系统可以应用在陆用导航（GPS、罗兰C、里程计）、水下导航（多普勒计程仪、基线系统）、航空航天以及无人系统导航等领域[7-9]，然而，实现惯性基组合导航的关键技术就是组合滤波方法[10]。

在现代滤波技术中，1995 年由S.J.Julier 和J.K.Uhlmann 提出的无迹卡尔曼滤波算法（Unscented Kalman Filter，UKF）一直是研究的热点，该算法通过UT 变换可以不忽略泰勒展开的高阶项，从而在非线性系统中有较高的估计精度和稳定性，受到了广泛的关注[11]。在捷联惯性基组合导航的实际应用中，估计的精度与实时性都是需要考虑的问题，UKF 不太大的计算量与较高的精度导致其成为了一种可行非线性的滤波方法，这也是其成为研究热点的原因之一。

在捷联惯性基组合导航实际应用中，捷联惯导自身比较稳定，不易受到干扰，而环境情况复杂多变，使得量测量难以避免的会被污染、干扰，这会对UKF的精度造成较大的影响，甚至导致滤波器的发散，进而影响到组合导航的效果。比如在城市中使用SINS/GPS 系统，可能存在卫星受到信号遮挡、信号受到干扰的情况；在水下使用SINS/DVL 系统，可能存在水流速或者水底地形的变化导致的测速异常等问题。如何提高滤波的抗干扰能力，提升组合导航系统的稳定性是UKF 在实际应用中必须要解决的问题。传统的鲁棒方法是通过增加量测噪声矩阵的权重以削弱野值对滤波的影响，但是这样会牺牲滤波一定的估计精度[12]。文献[13]对鲁棒滤波在初始对准动基座中的应用进行了研究，文献[14]对改进的Huber 鲁棒滤波进行了研究，通过文献[15]使用支持向量回归的方法提高组合导航系统的鲁棒性。

针对捷联惯性基直接法组合导航系统实际使用中出现的量测量中出现野值的问题，本文提出一种基于一类支持向量机辅助的适用于捷联惯性基组合导航的鲁棒UKF 算法（Support Vector Machine-Adaptive UKF，SVM-UKF）。本方法首先使用一类支持向量机（Support Vector Machine，SVM）建立滑动窗，来辨别滤波中的新息是否为异常，对于正常新息不予处理，对于异常的新息采用指数加权的方法得到新的“正确”新息以替代野值新息，这样不但可以修正量测值，还可以提高该情况下滤波的估计精度，提高系统的鲁棒性，根据江试实验数据，对SINS/GPS 系统使用SVM-UKF 与常规UKF，RUKF 滤波组合导航的精度进行比较。实验结果表明，在量测量有野值污染的情况下，SVM-UKF 具有更高的估计精度。

1 基于一类SVM 的野值识别与处理

对于量测量中野值的辨别，一类SVM 具有适用于小样本，非线性等特点，只需要正常工作的小样本数据就可以进行模型的训练，非常适用于野值的辨识。一类SVM 本质是通过在特征空间中寻找超平面对正常样本与异常样本进行分离，如图1 所示。

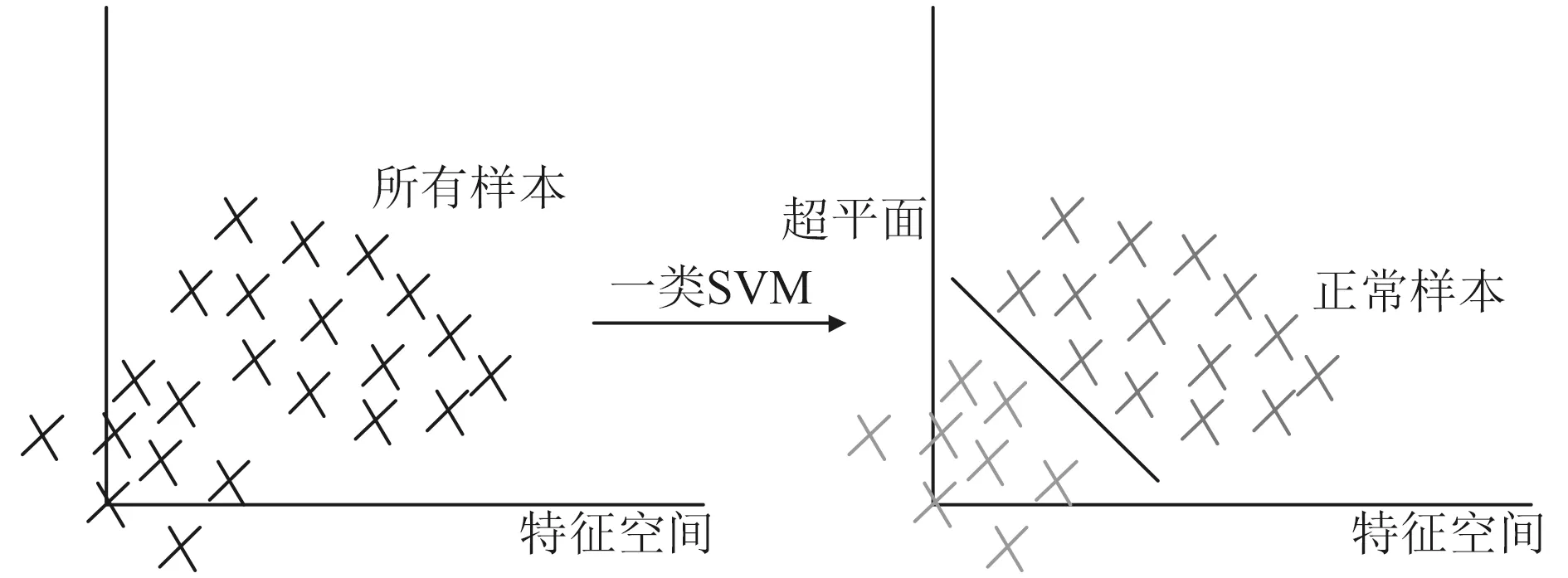
图1 一类SVM 分类基本原理图Fig.1 Graphical illustration of 1-class SVM

1.1 训练方法

一类SVM 的在线训练流程如下：

1）构建新息样本滑动窗

选取n个连续的不含野值的新息数据组作为训练信息样本滑动窗X=[x1,x2,···,xn]T,式中x表示新息。规范化训练新息滑动窗中每一个向量x。对规范化后的新息滑动窗进行主元分析得到目标向量矩阵Y：

式中：PPC=[p1,p2,···,pn]∈RN×l表示主元矩阵；y为支持向量；l为特征空间的维数。

2）训练一类SVM 模型

根据新息样本滑动窗训练得到的目标向量矩阵Y，训练一类SVM 模型为：

约束条件为：

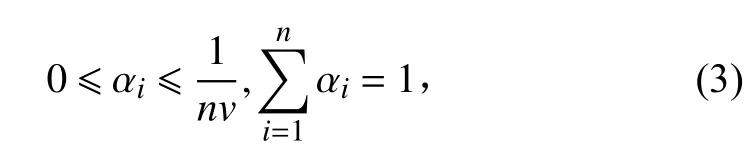
式中：α=[α1,α2,···,αn]T表示优化权值向量；Hij=K(yi,yj)，yi,yj∈Y，K(yi,yj)=e-‖xi-x j‖2/2σ2为核函数；v∈{0,1}是置信水平，用来表示允许训练新息样本出现错误被分类的程度。

3）计算偏移量

式中：b为偏移量；ns为y的个数。设定置信水平v的值，将新息样本滑动窗中的新息按从大到小的顺序排列，若验证数据样本的大小为n，则取第v×n个新息值为阈值Jn。

1.2 检测方法与野值处理

1）计算目标向量

将待检测新息数据x′，加入到新息样本滑动窗X中得到新样本，对x′进行规范化，根据式（1）得到目标向量：

2）计算距离检测量

本文采用文献[16]提出的使用一类SVM 模型的相反数作为检测量的方法，计算距离检测量为：

2）野值的识别与处理

1）新息的野值识别

若F(t)＜Jn，则新加入的新息x′为正常值；若F(t)＞Jn，则可以认定新息x′为野值，证明相对应的量测值为野值。

2）野值处理

传统的处理方法大多为将野值剔除，如果有数量较多的野值，剔除的方法有可能造成滤波的估计精度下降甚至发散。本文采用指数加权的方法，通过对滑动窗内正常的新息进行赋权，估计出野值新息处的“正确”新息，以替代野值新息。按照时间轴距离野值越近的新息权值越高，越远的新息权值越低，目的是使得越靠近野值的正常新息越能在对野值新息的估计中占有更大的比重。

权值系数应满足

权值系数因子为d=[(1-r)/(1-rn-2)]，其中r为遗忘因子，根据经验通常取0.95～0.99。

这样可以得到滑动窗内所有权值系数计算公式

通过权值系数可以估计出“正确”新息替代野值新息

这样通过指数加权就可以消除量测值野值对滤波效果影响。与传统的直接对量测值野值进行剔除的方法相比，该方法不影响滤波的量测更新，避免了滤波由于缺少量测更新造成的估计精度急剧下降甚至发散的情况。野值识别与处理的示意图如图2 所示。

图2 野值识别与处理方法示意图Fig.2 Identification and processing of outliers

1.3 SVM-UKF 算法

式中，xk表示k时刻的状态量，yk表示k时刻的量测量，wk-1～N(0,QK-1)为 系统噪声，rk-1～N(0,RK-1)为量测噪声，f(·)表 示捷联惯导基本方程，h(·)为量测模型，对h(·) 进行离散化处理可以得到H(·)。

SVM-UKF 算法流程如下：

1）时间更新

使用UT 变化构造sigma 点χk-1(i)=sigma(,Pk-1)，

通过系统模型更新得到 χk/k-1(i)，

状态预测均值与协方差为：

2）量测更新

计算新息并代入滑动窗：

若新息为野值，使用指数加权计算替代值后代入量测更新：

若新息为正常值，直接进入量测更新：

2 实验及分析

通过实验对所研究的SVM-UKF 方法估计效果进行评价。实验采用位置作为量测量SINS/GPS 松组合方式。

实验采用激光陀螺捷联惯导与GPS 组合实验数据来比较3 种算法的估计效果。该实验中采用激光捷联惯导系统的输出数据，激光陀螺漂移约为0.01°/h，加速度计零偏约为5×10-5g。惯导IMU 更新率为200 Hz，GPS 接收机更新率为1 Hz，水平速度误差小于0.1 m/s，位置误差小于2 m。

初始速度姿态位置由激光捷联惯导提供。

实验过程共10 000 s，本文选取5 800～6 700 s 的900 s 数据进行研究，该段中航行轨迹见图3，五角星表示船的初始位置，圆点表示船的末端位置。在GPS输出中每隔60 s 加入800 m 的位置误差模拟GPS 出现野值，以未加入野值的SINS/GPS 组合导航系统的结果作为参考基准，由于航海更关注位置与航向，因此给出组合导航的位置与航向估计效果如图4～图6 所示。

图3 实验船行轨迹图Fig.3 Trajectory map of river trial

图4 3 种滤波方法的经度估计误差Fig.4 Longitude estimation error of three filters

图5 3 种滤波方法的纬度估计误差Fig.5 Latitude eestimation error of three filters

图6 3 种滤波方法的航向估计误差Fig.6 Yaw estimation error of three filters

图4 与图5 表示了位置的估计结果，可以看到UKF受到野值的干扰已经发散，RUKF 与SVM-UKF 则表现出较好的估计效果。表1 给出了不同算法的位置、航向、东向、北向速度的RMSE 统计数据结果。由表1可以看出，RUKF 方法的位置误差为4.968 m，航向误差5.43′，北向速度估计误差0.08/s，东向速度估计误差0.07 m/s，SVM-UKF 方法的更好，位置误差和航向误差分别为2.474 m 和3.34′，北向、东向速度估计误差为0.04 m/s 与0.06 m/s。

表1 位置估计误差均方根误差Tab.1 RMSE of position and yaw error

根据实验结果，可以得出结论。在位置估计中，虽然RUKF 有一定的鲁棒性，但野值以及鲁棒算法还是影响了滤波器的估计精度，SVM-UKF 的估计效果比RUKF 提高50.2%。分析航向的估计结果可以发现，RUKF 虽然具有一定的鲁棒性，由于受到野值的干扰，SVM-UKF 的估计效比RUKF 提高38%。在速度估计方面，北向速度的估计精度SVM-UKF 比RUKF提高了50%，东向速度的估计精度SVM-UKF 比RUKF 提高了14.2%。

3 结 语

捷联惯性基组合导航中，量测值存在野值的情况时有发生，这个问题都会导致UKF 的估计精度下降。针对这些问题，本文提出了一种基SVM-UKF 算法。通过使用一类支持向量机训练滑动窗，按照新息是否为进行分类，对于异常的新息采用指数加权的方法进行估计，使用新的估计值替换野值。进行了船载实验对SINS/GPS 系统进行算法的性能检验。通过与UKF，RUKF 相比较，证明了算法的有效性，得到结果：在实验中，SVM-UKF 对比于RUKF，位置估计精度、航向估计精度分别提高了50.2%与38%，北向、东向速度对比于RUKF 分别位置估计精度，航向估计精度提高了50%与14.2%。