不同工况下有限长圆柱绕流实验测量及分析
2021-07-06梁圣召周军伟
梁圣召,周军伟,梅 蕾
(哈尔滨工业大学(威海)船舶与海洋工程学院,山东 威海 264209)
0 引 言
不同长径比、倒立入水的有限长圆柱流体流动特性对很多工程应用,包括浮式海上结构和桥梁涡振都有重要的研究价值。因为有限长圆柱的尾流和自由端的流动相当复杂,仅用实验方法不能满足相似参数和相似定律的要求,而且各项数据的测量以及尾流和自由端流动状态的观察比较困难。实验的这些不足可以由数值模拟来补充,但是截至目前,研究不同长径比倒立入水的有限长圆柱绕流流动特性的文献还不够充分。
早期的研究以实验为主,Okamoto 和Yagita[1]通过测量长径比AR=1-12.5 圆柱表面的压力分布得到了圆柱平均阻力系数,并分析了自由端的分离现象。H.Akilli和D.Rockwell[2]利用粒子图像测速法(PIV)对倒立入水的长径比为AR=1 和AR=2 的有限长圆柱进行了研究,研究结果形象解释了大尺度漩涡的形成。J.R.Chaplin等[3]在雷诺数Re与傅汝德数Fr的比值恒等于2.79×105的条件下对有自由液面的倒立入水圆柱在拖曳水池中进行了阻力实验研究。张荣誉[4]实验研究了具有自由液面的圆柱绕流现象,测量了不同Fr数工况下尾流场的变化规律。
随着CFD 技术的发展,Lee 等[5]采用CFD 方法(大涡模拟)对2 种长径比AR=2.5 和10 的壁面固定的有限长圆柱进行了数值模拟研究。Afgan 等[6]也采用大涡模拟在雷诺数Re=2×104和长径比AR=6 和10 的情况下对壁面固定的有限长圆柱进行了研究。Guilherme F.Rosetti 等[7]在雷诺数Re=4.3×104和傅汝德数Fr=0.31 的条件下,对长径比ui=2倒立入水的有限长圆柱从实验和数值模拟两方面进行了研究。发现自由表面的存在会影响流动,但是占主导作用的还是自由端的影响。M.A.Benitz 等[8]在雷诺数Re=2 900 和傅汝德数Fr=0.65 的条件下,对长径比从1~19 倒立入水的有限长圆柱进行了实验研究,并用大涡模拟进行了对比验证。
目前学者们已经探讨了部分雷诺数,傅汝德数以及长径比下圆柱绕流的流动特性,同时开展了以大涡模拟为主的数值方法验证。但是Re和Fr的覆盖范围还不够全面,探讨还不够充分。本文首先采用实验测量和数值模拟相结合的方法对不同长径比圆柱的阻力系数进行对比分析,而后对有限长圆柱的尾流场特征进行讨论,为海工结构设计提供一定的数据参考。
1 数值模拟方法
1.1 控制方程
对于三维非定常不可压缩粘性流动,其连续性方程和动量方程为:

式中:ui,uj为速度分量;p为压力;v为总的流体运动黏性系数,表示为层流黏性系数与湍流黏性系数之和,其中湍流黏性系数由湍流模型获得;fi为外力分量。
本文采用Wilcox 的k-ω湍流模型,具体可参照文献[9]。基于CFX 求解器实现方程的求解。
1.2 计算域模型
几何模型如图1 所示,长×宽×高为4 m×2 m×1.2 m,相当于80D×40D×24D,其中特征长度D=0.05 m。坐标原点在圆柱底面的中心处。计算域入口距离圆柱中心为20D,出口距离圆柱中心60D,两侧面距离圆柱中心20D。
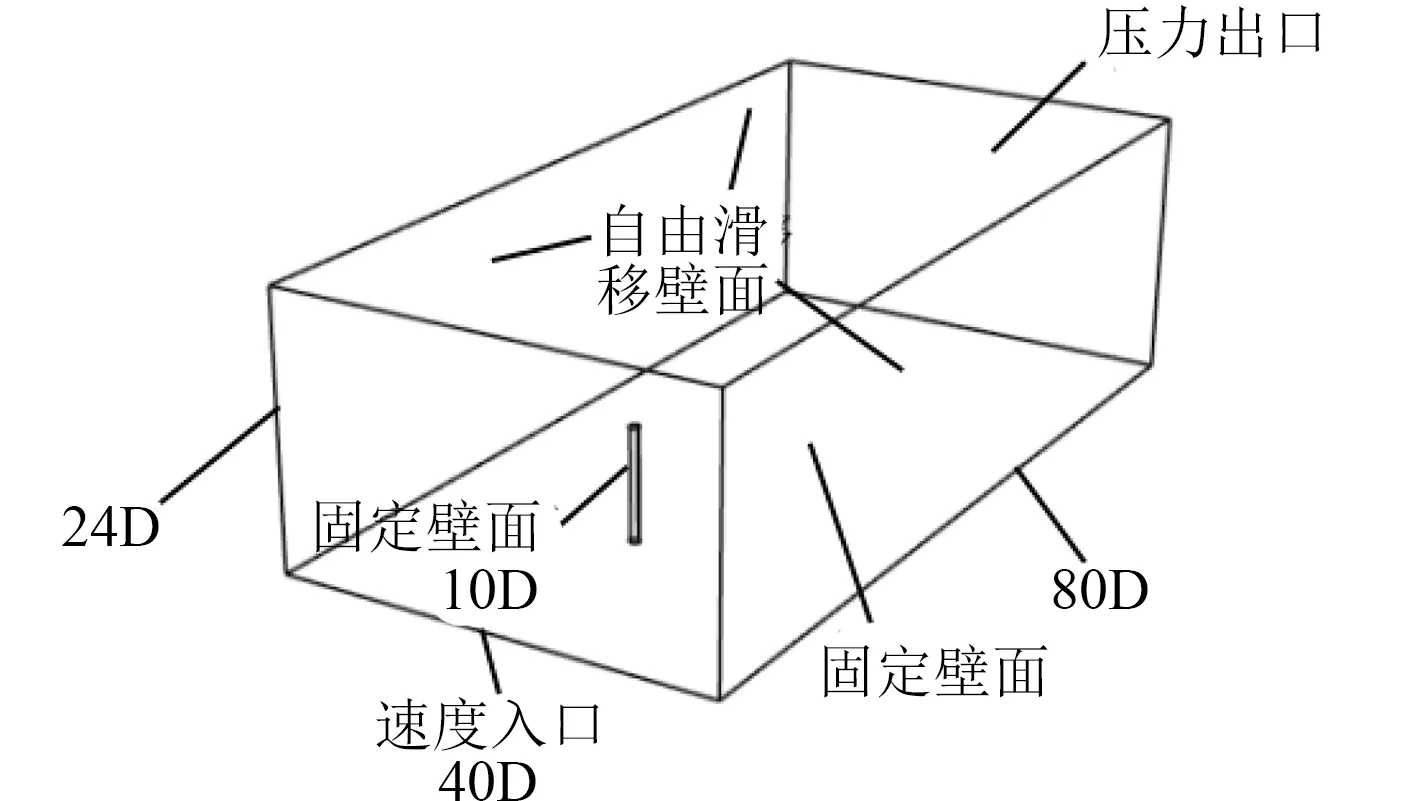
图1 有限长圆柱绕流几何模型Fig.1 Model of computational domain for finite cylinder
流体域进口设定为速度进口(inlet);出口设定为压力出口边界(outlet);流体域上表面以及2 个侧面均设定为自由滑移壁面(free slip wall),下表面设置为无滑移壁面(no slip wall);圆柱表面包括自由端面设定为无滑移壁面(no slip wall)。
1.3 数值方法验证
1)分别进行网格数量和湍流模型对计算结果和计算时间的对比分析。计算条件为:流场无穷远处的均匀来流速度为U=0.6 m/s,流体为水,密度ρ=1 000 kg/m3,运动粘性系数ν=10-6m2/s,计算得雷诺数Re=3×104,时间步长0.001 s。网格在圆柱周向均布100 个节点,法向挤出20 层,线性增长率1.3。近壁面处保证y+<2。3 种网格密度采用同样的加密区域7D×3D,采用四面体、棱柱型与六面体网格相结合的方式,以改善网格质量,计算域网格划分如图2 所示。3 套网格分别命名为Coarse,Medium 和Fine,网格数分别为49 万、119 万和200 万。表1 为k-ω湍流模型不同网格密度条件下,以及在Medium 网格下分别采用DES,k-ω和k-ε三种湍流模型所得到的升阻力系数以及计算所耗时间。可以看出当采用k-ω模型时,使用Medium 和Fine 网格,Cd计算结果相差2.7%,Cl计算结果相差9.93%,但是计算时间相差1 倍,所以Medium 网格数计算精度足够。而在Medium 网格数下,k-ε的计算结果与DES 和k-ω的结果相差较大,DES 和k-ω的计算精度最大误差在15%以内,但是计算时间相差近1 倍。综合考虑计算精度与计算时间成本,本文选取Medium 网格数119 万,湍流模型选择k-ω。

图2 不同密度的网格划分Fig.2 Grid with different densities

表1 不同网格密度和湍流模型的比较Tab.1 Numerical results of different mesh refinement and different turbulence model
2)鉴于文献在研究相关问题时多采用大涡模拟(LES)湍流模型,为了进一步验证本文计算模型的可用性,在同等初始条件下,对不同工况及长径比的有限长圆柱进行计算,并与前人所做相近工况的实验和数值模拟结果进行对比。首先,本文计算和实验结果与前人所做相近工况的实验和数值模拟结果进行对比,如表2 所示。可以看出:在长径比AR=6,雷诺数Re=3×104工况下,本文计算结果比H.Sakamoto[10]的实验值大6.59%,实验结果比H.Sakamoto[10]的实验值小12.3%;在长径比AR=10,雷诺数Re=3×104工况下本文的计算结果比LEE[5]的计算值大5.18%,实验值比其小2.56%。与相似工况下的文献结果的误差均在可以接受范围内。同时,在长径比AR=10,雷诺数Re=3×104工况下,本文的实验结果与计算结果也进行了对比,如图3 所示。可知实验值与计算值的升阻力系数时程图比较接近,而横流向的振动频率约是顺流向振动频率的2 倍,这与王晓聪[11]的研究结论相符,也侧面佐证了本文研究的准确性。最终选取k-ω湍流模型进行数值分析。

图3 实验与计算升阻力系数时程图Fig.3 Distribution of the time-dependent lift and drag coefficient for EXP and CFD
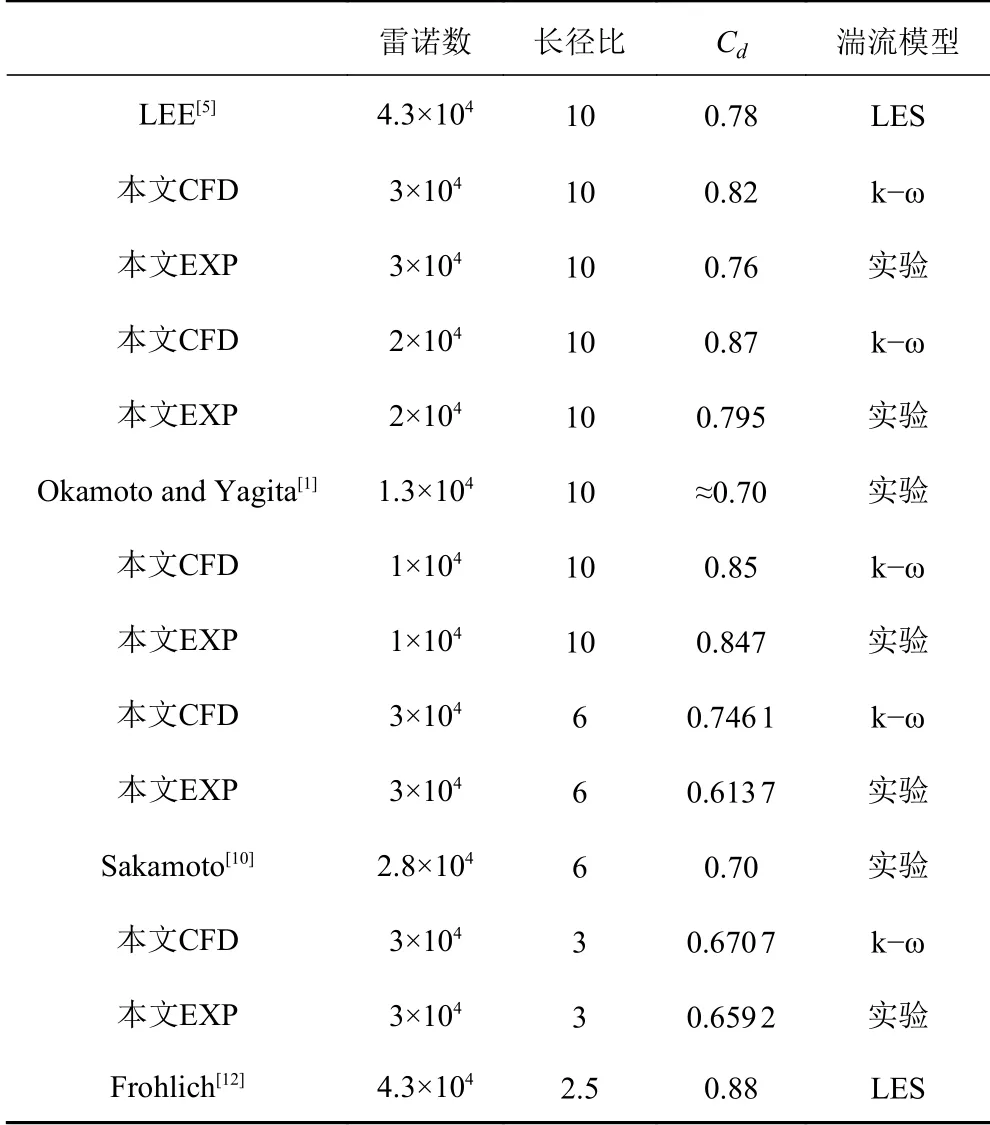
表2 不同作者相似工况计算结果Tab.2 Calculation results of similar conditions for different authors
2 实验测试
实验在哈尔滨工业大学(威海)海洋工程学院的循环水槽实验室进行,三维模型如图4 所示。实验所用圆柱材质为均质6061 铝合金,直径50 mm,圆柱表面经过高速车削处理,以达到较小的粗糙度。实验中,测力单元处于水面之上,而底板略低于水面,以尽量减小自由液面对测量结果的影响。
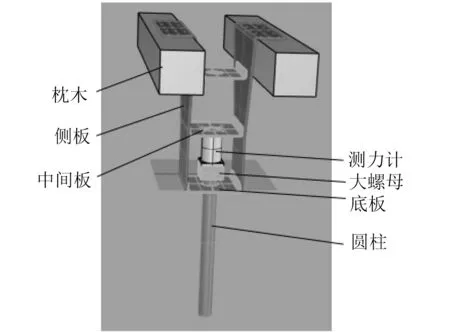
图4 三维模型Fig.4 3D model
实验来流速度U选择为0.2,0.4 和0.6 m/s,对应的雷诺数分别是1×104,2×104和3×104。测试3 个长径比的圆柱,其高度分别为H=150,300 和500 mm,对应长径比为AR=3,6 和10。实验中对测力计进行细致的标定,以保证测量结果的准确度。3 个不同的来流速度以及3 个长径比组合共9 组实验,每组实验进行4 次测量,取平均值。
3 结果与分析
3.1 阻力系数分析
将不同长径比下,数值模拟与实验研究所得阻力系数的均方根值进行对比,其与雷诺数的关系如图5所示。研究发现,当长径比AR=3,6 和10 时,阻力系数均随流速的增加有1 个逐渐减小的趋势,这与R.T.Gonçalves[13]的实验结果相一致,原因是流速越大,自由端对流动的影响越大。但阻力系数总体变化不大,表明在长径比大于3 的工况下,有限长圆柱绕流的阻力系数趋于平稳,其值在0.61 与0.86 之间。但同时也发现,本文的实验结果与数值模拟结果存在5%~25%的误差,其产生的原因有2 个,一是在实验过程中循环水槽存在槽体共振现象。而实验中阻力的最大值只有4N 左右,所以轻微的槽体振动也会对实验结果产生一定的影响。第2 个原因是本文数值模拟采用的是壁面固定式圆柱,而实验则是采用的“倒立入水”式。为了尽量减小自由液面对实验结果影响,实验中在与自由液面相切的位置增加了一块底板,防止液面波动对圆柱受力产生影响,但仍不能完全避免自由液面的影响。
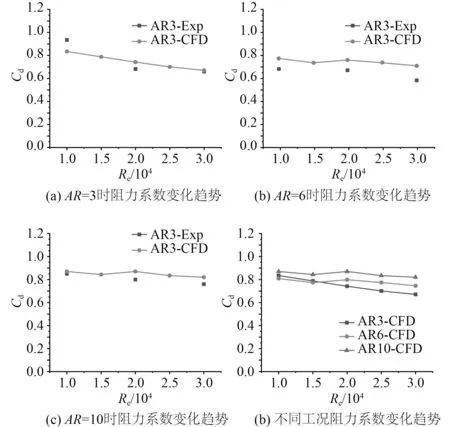
图5 雷诺数与阻力系数的关系Fig.5 Relationship between Re and drag coefficient
3.2 流场分析
流速U=0.6 m/s 工况下,长径比AR=3,6 和10 的三维流线图如图6 所示。长径比AR=3 的圆柱在展向几乎没有涡流,也没有漩涡脱落。而长径比AR=6 和10 的圆柱在展向则有明显的涡流以及漩涡脱落现象。同时发现,当长径比AR=3 时,圆柱后方有极其混乱的湍流,其影响范围从圆柱自由端一直到固定壁面。分析原因应该是当流体流经圆柱自由端时产生“下洗”现象,当长径比较小时,“下洗”运动直接冲击到圆柱的根部,同时也破坏了圆柱后方有规律的漩涡脱落,产生了极其混乱的湍流;当长径比AR为6 和10 时,圆柱后方均有一个较小的回流区,并且也会产生“下洗”现象,但因为长径比较大,“下洗”运动只能影响圆柱的自由端,破坏自由端附近的漩涡脱落,而对圆柱中间以及根部没有影响。而且相比固定壁面处,圆柱中间部分的漩涡脱落更为明显,说明固定壁面的存在一定程度上抑制了漩涡脱落的产生。即圆柱的长径比越长,“下洗”运动影响的长度占展向长度的比例就越小,所以随着长径比的增加,阻力系数会缓慢增加。而有限长圆柱绕流的阻力系数比无限长圆柱低的主要原因同样可能是有限长圆柱自由端的存在使得流体可以绕过自由端流动,而在无限长的情况下流体只能从两侧绕着圆柱流动。

图6 不同长径比三维流线图Fig.6 3D streamline with different AR
为了能清晰地得到圆柱后方漩涡脱落的流动,采用Q准则(Q-criterion)对尾涡进行可视化。Q的定义为:
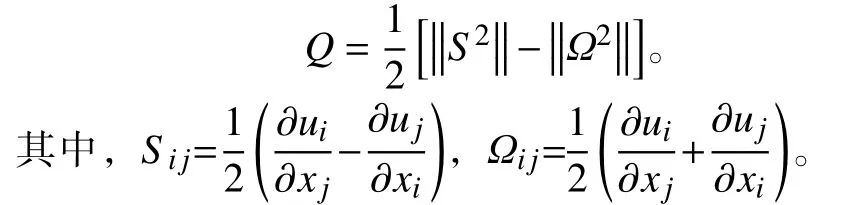
不同长径比下三维涡对比如图7 所示。可以看出,当长径比AR=3 时,漩涡结构没有震荡,因为其长径比较小,所以自由端产生的高涡量控制了整个圆柱体的流动行为;当长径比AR=6 和10 时,出现了不同的漩涡脱落区域;漩涡在圆柱的中下部周期性震荡,并且几乎与圆柱平行;在圆柱的中上部,漩涡的周期性震荡仍然存在,但是不再与圆柱平行,而是呈现出一定的角度。这种现象可能是由圆柱中上部分不同展向位置处的振幅不同引起的。长径比AR=10 时不同流速下三维涡对比如图8 所示。随着流速的增加,涡黏度最大值也在增加。当从0.2 m/s 增加到0.4 m/s时,涡黏度最大值增加了92.4%,从0.4 m/s 增加到0.6 m/s时,涡黏度最大值增加了12.4%。说明随着流速的增加,涡黏度最大值的增速在逐渐降低。从图中也可以看出,随着流速的增加,圆柱后方不同位置处涡的相互作用也增强了。

图7 不同长径比下三维涡粘度图(Q=7)Fig.7 3D Eddy viscosity with different AR(Q=7)

图8 长径比AR=10 时不同流速下三维涡粘度图(Q=7)Fig.8 3D Eddy viscosity at different velocity when AR=10(Q=7)
4 结 语
本文对雷诺数Re=1×104-3×104和长径比AR=3,6 和10 的三维有限长圆柱绕流进行了数值模拟和实验研究,得到如下结论:
1)在所涉及的工况范围内,采用k-ω模型对三维有限长圆柱绕流数值分析是可行的,计算稳定,耗时少,计算误差在可以接受范围内。
2)当长径比AR=3,6 和10 时,数值模拟和实验的结果均表明,阻力系数随流速的增加有一个逐渐减小的趋势,数值模拟结果稳定在0.8 左右,实验分析得到的阻力系数落在0.61~0.93 区间内。表明在长径比大于3 的工况下,有限长圆柱绕流的阻力系数趋于平稳。
3)圆柱自由端的存在使流动具有更明显的三维特性,自由端的“下洗”作用会绕过自由端冲击圆柱后方的漩涡脱落,导致阻力系数小于无限长圆柱。在长径比AR=6 和10 时,出现了不同的漩涡脱落区域。漩涡在圆柱的中下部周期性震荡,并且几乎与圆柱平行。在圆柱的中上部,漩涡的周期性震荡仍然存在,但是不再与圆柱平行,而是呈现出一定的角度。
4)涡黏度最大值随着流速的增加也在增加。当从0.2 m/s 增加到0.4 m/s 时,涡黏度最大值增加了92.4%,从0.4 m/s 增加到0.6 m/s 时,涡黏度最大值增加了12.4%。
