AOR Iterative Method for Coupled Lyapunov Matrix Equations

(1.Department of Mathematics,Shanghai University,Shanghai 200444,China;2.Nanyang Vocational College of Agriculture,Nanyang 473000,China)

Abstract:An AOR(Accelerated Over-Relaxation)iterative method is suggested by introducing one more parameter than SOR(Successive Over-Relaxation)method for solving coupled Lyapunov matrix equations(CLMEs)that come from continuous-time Markovian jump linear systems.The proposed algorithm improves the convergence rate,which can be seen from the given illustrative examples.The comprehensive theoretical analysis of convergence and optimal parameter needs further investigation.

Keywords:Coupled Lyapunov matrix equations;AOR iterative method;SOR iterative method;Markovian jump systems

§1.Introduction

The coupled Lyapunov matrix equations(CLMEs)[7]

whereAiare system matrices,Piare unknown,Qiare arbitrarily given positive definite matrices(Qi＞0),andπijform the transition rate matrixΠ=[πij]N×N,which come from continuous-time Markovian jump linear systems[4]

wherex(t)∈Rnis the state vector,ρ(t)is a time homogeneous Markovian process that takes values in a finite discrete setS={1,2,...,N},andAρ(t)are system matrices,are significant to Markovian jump linear systems in stability analysis and stabilizing controller design[14].

As Feng etc.[3]showed that the stochastic stability of jump linear systems can be characterized by the existence of unique positive definite solutionsPiof CLMEs(1.1),it is important to investigate the solution of CLMEs theoretically and numerically[1,2,9–12,15,17,19,20].

In 1987,Jodar and Maritona[8]proposed a direct method for the coupled matrix equations,which is not good for large scale systems.Subsequently,various kinds of iterative methods were studied by many authors.Borno[1]firstly developed an implicit iterative algorithm which needs to solve some standard Lyapunov equations at each iteration.Then implicit iterative methods were widely investigated[11,17–19],and the algorithm in[18]is a weighted implicit iterative algorithm which significantly improved the convergence with appropriate weighting parameters.As the implicit iterative algorithms are costly for high dimension case because of the requirement of solving standard Lyapunov equations at each step,explicit iterative algorithms,for example,the gradient-based methods[2],were paid much attention[14]then.In[22],Zhang constructed some reduced-rank gradient-based iterative algorithms for generalized coupled Sylvester matrix equations,which also can be used to solve the coupled Lyapunov matrix equations[14].In[6],He et al.established a policy iterative algorithm for the coupled Lyapunov matrix equations.And as the classical Smith iterative method was used to solve standard Lyapunov equations[16],Sun,Zhang and Fu[14]discussed accelerated smith iterative algorithms for coupled Lyapunov matrix equations.

It is well-known that SOR(Successive Over-Relaxation)iterative method is superior to the classical iterative methods such as Jacobi,Gauss-Seidel,Smith methods[21].Recently,Wu,Sun and Zhang[19]suggested an SOR(Successive Over-Relaxation)iterative algorithm

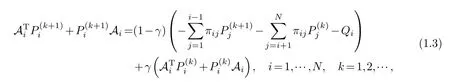
whereAi=Ai+0.5πiiI,Iis identity matrix,for solving CLMEs(1.1)numerically.With a relaxation parameterγin this algorithm,the convergence performance can be improved.

And,Hadjidimos[5]set up an accelerated overrelaxation(AOR)iterative method for solving linear systems by introducing one more parameter than SOR method to increase the convergence rate which will converge faster than any other method of the same type with appropriate parameters(thus,to determine such parameters that the method has the fastest convergence rate,the optimal parameters[5,13,21],is also an interesting topic).Thereafter,AOR method has been widely used to solve linear systems of equation(s)[13].

This note gives an AOR iterative scheme for solving CLMEs(1.1)with an additional parameterωcompared to SOR algorithm(1.3),followed by illustrative numerical examples which show the effectiveness and efficiency.The contribution is that the authors discuss the numerical solution of CLMEs(1.1)in a different view(using two overrelaxation parameters)from SOR and other existing methods,which accelerates the convergence rate and improve the convergence(iterations and CPU time)much.In general,as stated in[13](which is a special discussion for the optimal parameters of the AOR iteration),the determination of the optimal parameter is a difficult topic(in many cases,the optimal parameter cannot be obtained theoretically,for example,in[19],Wu,Sun and Zhang just only provided the optimalγfor SOR in the caseN=2,even though,which is still difficult for AOR as there are two parameters).Therefore,the theoretical analysis of the optimal parameters for AOR needs further investigation and was not involved in this note.It will be presented as a follow-up of separate work.

§2.AOR method for CLMEs

For matricesAi,i=1,···,Nin(1.3)and two scalarsωandγ,the following hold

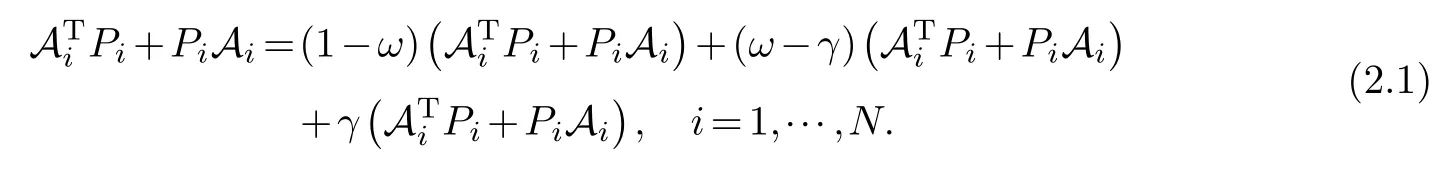
With the treatment

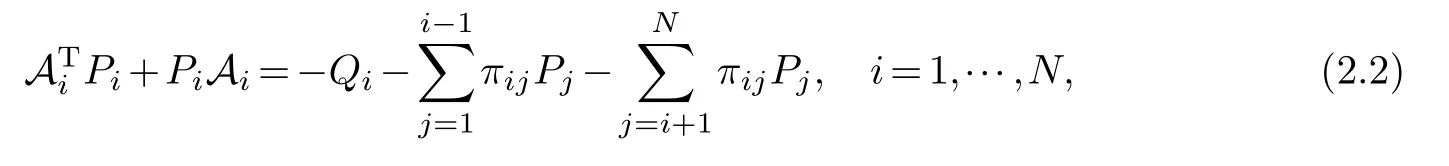
suggested by Borno[1],(2.1)can be changed into

By(2.3),an accelerated overrelaxation iterative scheme,referred to as AOR,can be established for solving CLMEs(1.1)as follows,

Similar to Theorem 1 and Theorem 3 in[19],a convergence result for method(2.4)can be obtained as the following theorem.

Theorem 2.1.For stochastically stable Markovian jump linear system(1.2),and the corre-sponding CLMEs(1.1)with Qi＞0,i=1,···,N,starting from arbitrary,i=1,···,N,theiterative sequencegenerated by AOR iterative scheme(2.4)with-1＜γ＜1monotonically converges to the unique positive definite solution(P1,P2,···,PN)of(1.1).

Remark 2.1.Whenω=γ,the AOR method(2.4)is reduced to algorithm(1.3).

Remark 2.2.If the number of the subsystems is N=2,then,like SOR algorithm in[19],some necessary and sufficient conditions can be presented for the convergence of AOR method(2.4),and the optimal relaxation parametersωandγcan be deduced,but as it is a max-min problem of a two-variable function,the theoretical analysis is much more complicated,which will be conducted in a separate topic.

The AOR algorithm is as follows.

AOR Algorithm Require:N,Ai,Π,Qi,ω,γ,i=1,···,N Ensure:Pi,i=1,···,N 1:while error＞given∈do 2: for i=1:N do 3: P(k+1)i =LYAPA,(1-ω)-i-1j=1πijP(k+1)j -Nj=i+1πijP(k)j-Qi4: +(ω-γ)-i-1j=1πijP(k)j-N j=i+1πijP(k)j-Qi+γimages/BZ_38_1505_1321_1530_1362.pngATi P(k)i+P(k)i Ai5:end for 6:end while where LYAP(A,Q)solves a standard continuous Lyapunov matrix equation ATX+XA=Q.

§3.Illustrative examples

One example from[19]and another larger in different sizes are discussed to illustrate the proposed AOR method(2.4)with iterative error defined by

and iteration stopping criterione(k)＜10-13.All implements using Matlab run in a Windows 7 DELL laptop with Intel 2.80GHz CPU and 8.00GB RAM.

Example 3.1([19]).Consider CLMEs(1.1)with N=3,where

the transition rate matrix is

and Qi=I,i=1,2,3,are identity matrices.

Fig.1 presents the convergence performance of the AOR method(2.4)compared with the SOR algorithm in[19]under zero initial condition(=0,i=1,2,3),where the iterationskvsγare shown by taking the sameγfor two methods andω=-0.05 for AOR.This figure shows that AOR iterative method(2.4)is convergent if-1＜γ＜1 as SOR method,and for a fixedωAOR has less iterations than SOR whenγis greater than a certain value(which is the optimalγ=-0.0511 of SOR,see[19]),thus,it would be interesting to investigate the optimal parameters for AOR.

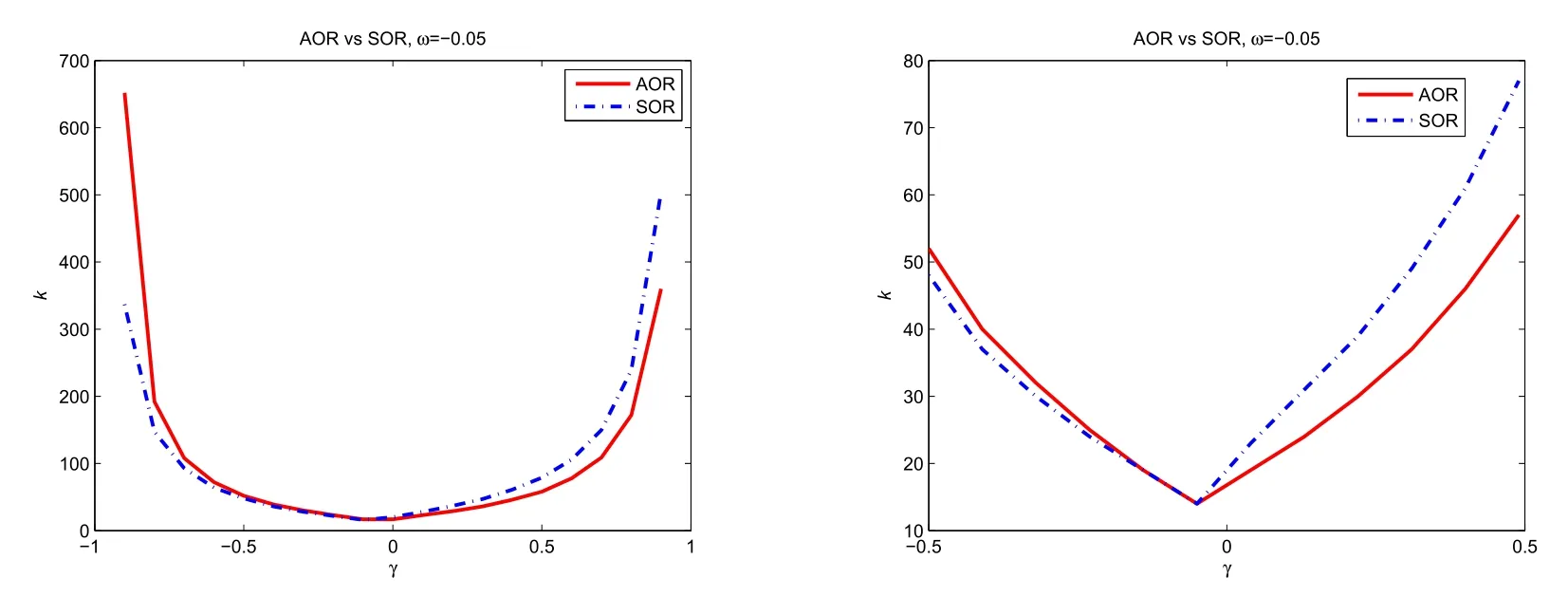
Fig.1 The convergence performance of AOR and SOR methods with different relaxation parameters

Withω=-0.06311,γ=-0.03755 for AOR method(2.4)and the optimalγ=-0.0511 for SOR method(1.3),the iterations(k),CPU time(t)and iterative error(e(k))for both methods are listed in Table 1.

AOR SOR ω γ k t e(k) k t e(k)-0.06311 -0.03755 13 0.0360 8.3101e-014 14 0.0439 2.9086e-014

It can be seen from Table 1 that AOR needs less iterations and CPU time,which implies that with the optimal parameters AOR could converge faster than SOR.

Example 3.2.Consider CLMEs(1.1)with N=2,where

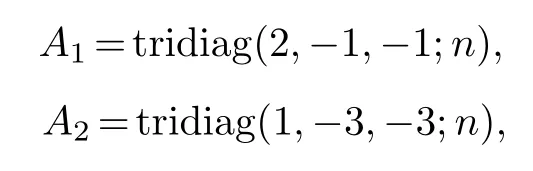
are n×n symmetric tridiagonal matrices,the transition rate matrix is

and Qi=I,i=1,2,are identity matrices.

With differentnand the optimal parameterγoptfor SOR method,the iterations(k),CPU time(t)and iterative error(e(k))for AOR method(2.4)and SOR method(1.3)are listed in Table 2.

AOR SOR n ω γ γopt k t e(k) k t e(k)5 -0.0012 0.0006 -0.0008 7 0.0316 8.2486e-014 8 0.0328 5.3337e-015 10 -0.0012 0.0006 -0.0076 10 0.0331 2.2968e-014 9 0.0346 6.6840e-014 15 -0.0012 0.0006 -0.0138 12 0.0367 1.8818e-014 13 0.0369 6.0257e-014 20 -0.0012 0.0006 -0.0200 10 0.0371 2.8360e-014 12 0.0397 4.9946e-014 25 -0.0012 0.0006 -0.0679 9 0.0486 3.0071e-014 16 0.0504 2.7824e-014 30 -0.0012 0.0006 -0.0889 11 0.0507 5.0800e-014 17 0.0566 5.4789e-014 35 -0.0012 0.0006 -0.1779 - - - - - -40 -0.0012 0.0006 -0.1668 12 0.0699 9.6481e-014 29 0.0936 8.8793e-014 45 -0.0012 0.0006 -0.2864 11 0.0658 4.4134e-014 38 0.1735 6.7415e-014 50-0.00120.0006×-- - -- -55 -0.0012 0.0006 -0.2745 16 0.1102 9.8575e-014 - - -60 -0.0012 0.0006 -0.1990 - - - - - -65 -0.0012 0.0006 -0.4060 13 0.1341 9.6172e-014 - - -

Table 2 shows that for different sizes of CLMEs(1.1)in Example 3.2,even though with the same parametersω=-0.0012,γ=0.0006,AOR almost always converge faster than SOR with the optimal parameterγopt.The only exception isn=10 where the iterationskof AOR is a bit larger,but in that case,the CPU timetis still less and the iterative errore(k)is smaller,which means that with appropriate parameters AOR could still converge faster than SOR(in fact,withω=-0.011,γ=0.0006,AOR has iterationsk=9,CPU timet=0.0330 and iterative errore(k)=1.8895e-014 in the casen=10).And there is an interesting point that withnincreasing the SOR method has iterationskincreasing while the AOR method has oscillating iterations.This confirms that exploring the optimal parameters for AOR method would get much better convergence rate.

§4.Conclusion

In summary,this note investigates the AOR iterative method for solving CLMEs(1.1).Convergence result and the numerical examples show that the proposed AOR algorithm(2.4)is effective and more efficient than SOR algorithm(1.3),and from Example 3.2,it can be seen that good overrelaxation parameters may be selected through small scale systems by searching(almost all tested cases are good using the same parameters there).Anyway,further interested work would be comprehensive analysis of convergence and the optimal parameters for AOR method.

Acknowledgements

The authors thank the editor and the reviewers a lot for their invaluable advice and suggestions which greatly improve the quality of the paper.