Neighborhood-Based Set-Valued Double-Quantitative Rough Sets

(College of Artificial Intelligence,Southwest University,Chongqing 400715,China)

Abstract:Double-quantitative rough approximation,containing two types of quantitative information,indicated stronger generalization ability and more accurate data processing capacity than the single-quantitative rough approximation.In this paper,the neighborhood-based double-quantitative rough set models are firstly presented in a set-valued information system.Secondly,the attribute reduction method based on the lower approximation invariant is addressed,and the relevant algorithm for the approximation attribute reduction is provided in the set-valued information system.Finally,to illustrate the superiority and the effectiveness of the proposed reduction approach,experimental evaluation is performed using three datasets coming from the University of California-Irvine(UCI)repository.

Keywords:Attribute reduction;Double quantification;Fuzzy similarity relation;Setvalued information system

§1.Introduction

Rough set model[9]proposed by Pawlak,is a mathematical theory for data analysis.However,the traditional Pawlak rough set can only handle discrete data,and it is impossible to process the quantitative information.In order to make the rough set model suitable for more kinds of data processing scenarios,many scholars have extended the rough set model from multiple perspectives.Yao et al.proposed the rough set decision model based on Bayesian risk analysis[13,14],Wong and Ziarko raised the 0.5-probability rough set model[10],Ziarko put forward a variable precision rough set model[21],Sun and Gong extended the variable precision probabilistic rough set model[11],Li and Xu considered two types of quantitative information on the basis of the probability rough set model and the degree rough set model,and proposed the the double-quantitative rough set model[5].From the results reported in[5],it could find that the double-quantitative rough set model has strong fault tolerance.The relative and absolute quantitative information are two kinds of quantification mythologies encountered in certain applications[3,12,18–20].

Attribute reduction is an important issue of knowledge discovery[7,8,15–17].As the information system often contains redundant attributes,it is necessary to obtain the necessary attributes of the information system to extract useful and important information,so as to improve the decision-making efficiency of the model[1,2,4,6].In this paper,we want to establish a double-quantitative rough set model in an information system with the set-valued data and discover the decision-making rules based on the proposed models,and then propose a lower approximation reduction algorithm for the model.

The paper is organized as follows.Related concepts are reviewed briefly in Section 2.In Section 3,we construct a fuzzy similarity relation in the set-valued information system,and derive the corresponding fuzzy similarity classes.And then present the neighborhood-based set-valued single-quantitative rough sets.In Section 4,we mainly discuss the neighborhood-based set-valued double-quantitative rough set models based on the fuzzy similarity relation.In Section 5,we develop the lower approximation reduction based on the presented double-quantitative rough set models,and provide the corresponding algorithm for the reduction method.In Section 6,we conduct a comprehensive analysis on the advantage and disadvantage for the single-quantitative and double-quantitative models.Finally,Section 7 covers some conclusions.

§2.Preliminary and basic concepts

This section briefly reviews the basic knowledge of Pawlak rough set,single-quantization models,and attribute reduction.In this paper,P(U)andF(U)represent the class of subsets and fuzzy subsets ofU,respectively.

Definition 2.1.Let(U,A,V,f)be an information system,R is an equivalence relation,for any X⊆U,the upper and lower approximation of the target set X are defined as

The SetPosR(X)is called positive domain ifPosR(X)=(X);the setNegR(X)is called positive domain ifNegR(X)=(X);the setBnR(X)is called boundary domain ifBnR(X)=.

Definition 2.2.Let(U,A,V,f)be an information system,X is the target set,B is an equivalence relation,the upper and lower approximation operators based on the thresholdα,βare defined as

where0≤β＜α≤1.(X),X is a probabilistic rough set(PRS)model.

Definition 2.3.Let(U,A,V,f)be an information system,for B⊆A,B is an equivalencerelation,given a parameter k to indicate the degree,which satisfies0≤k≤|U|,k∈R,Ris a set of real numbers,for any X⊆U,the upper approximation operator and the lower approximation operator are defined as

Definition 2.4.Let B be the coordination set of(U,A,F)for B⊆A,if RB=RA,and for any b∈B,exists RB-{b}/=RA,then B is the reduction of(U,A,F).For any information system(U,A,F),its reduction always exists,and the intersection of all reductions is called the kernel of the information system.

An information system can have multiple reductions,but the kernel is unique.

§3.Neighborhood-based set-valued single-quantitative rough sets

In this section,we mainly study how to construct neighborhood-based set-valued singlequantitative rough set(NB-SV-SqRS)models.The first step in model construction is to construct the fuzzy similarity relation on the set-valued information system,and obtain the corresponding fuzzy similarity classes.As we know,the distance between two objects could reflect the degree of difference for this two objects.In a sense,the greater the distance between two objects,the lower similarity degree between the two objects.It is necessary to construct a distance function.

Definition 3.1.Let S=(U,A,V,f)be a set-valued information system,xi and xj are two objects in U.If B⊆A,the distance dij of xi,xj about B is defined as:

where⊕is the symmetric difference operation of the set,if the value of p is different,the distance represented is different.Choose p=2at here.The distance function has the following properties:

(1)Non-negativity:dij≥0,

(2)Symmetric:dij=dji,

(3)Triangle inequality:dij≤dim+dmj.

It is clear that property(1),(2)was established,and now give the proof of property(3)by contradiction.Suppose∀xi,xm,xj⊆U,leta=|f(xi,ak)⊕f(xm,ak)|,b=|f(xm,ak)(xj,ak)|,c=|f(xi,ak)∪f(xm,ak)|,d=|f(xm,ak)∪f(xj,ak)|.Assume property 3 is not true,so

Equationacan be defined as

According to the knowledge of set theory can find thatA⊕B⊆(A⊕C)∪(B⊕C)andA∪B⊆(A∪C)∪(B∪C),thus

Accordingly

thus

Obviously,it can be seen that

Therefore

So,equationbis not existed,it’s also signify that equationais not established.In conclusion,property 3 is established.

In order to get the similar valuesijbetween the two objectxiandxjunder the attribute setBthrough the distance function,however the value ofsijshould be between 0 and 1,sodijneed to normalized.

Definition 3.2.Let(U,A,V,f)be a set-valued information system and B⊆A,dij is the distance between two objects xi and xj under the attribute set B,Dij is the distance between the two objects xi and xj under the attribute set A,then normalize dij to d*ij:

Definition 3.3.Let(U,A,V,f)be a set-valued information system and B⊆A,B is the neighborhood-based fuzzy similarity relationship of B,and its fuzzy similarity matrix S()is defined as:

where sij=1-d*ij represents the similarity value between the two objects xi and xj,and the relationshipis the fuzzy similarity relationship.

SupposeIis a identity matrix,S(B)satisfies the following two properties:

(1)Reflexivity:I≤S()(⇔sii=1).

(2)Symmetry:S()T=S()(⇔sij=sji).

ThusS() is a fuzzy similarity matrix,is proved by the fuzzy similarity relationship.

Definition 3.4.Let(U,A,V,f)be a set-valued information system and B⊆A,is the fuzzy similarity relation of B,for any∀x∈B,[xi]={y|y∈B∧x~By},[xi]is called the fuzzy similarity class of xi about the fuzzy similarity relationwhich is referred to as the fuzzy similarity class for short,abbreviated as[x].

(1)∀x∈A,[x]is a nonempty subset.

(2)∪{[x]|x∈A}=A.

The previous section explained how to construct a fuzzy similarity relation.The following will discuss how to construct two single-quantitative rough set models.The difference between the two models is that the introduced quantitative information is different.The introduction of relative quantitative information can construct a neighborhood-based set-valued probabilistic singlequantitative rough set(NB-SVP-SqRS);the introduction of absolute quantitative information can construct a neighborhood-based set-valued degree single-quantitative rough set(NB-SVD-SqRS).

Definition 3.5.Let(U,A,V,f)be a set-valued information system and B⊆A,is the fuzzy similarity,for any ∈F(U),F(U)represents the class of all fuzzy subsets of U,let0≤β＜α≤1,then the upper approximation operator and lower approximation operator of the probabilistic set-valued information system are

The upper approximation operator and lower approximation operator of the probabilistic set-valued information system can also be defined as

It can be seen that there is a strict containment relationship betweenand,which is.

At last he felt convinced, in his own mind, that he really had one, and was so delighted that he positively17 died of joy at the thought of having at last caught an idea

Definition 3.6.Let(U,A,V,f)be a set-valued information system and B⊆A,B is the fuzzy similarity relation of B,0≤k≤|U|,k∈R,for any∈F(U),then the upper approximation operator and lower approximation operator of the degree set-valued information system be defined as

The lower operators of degree set-valued information systemcan can also be defined as:

Obviously,compared with the classic rough set model,there is not strict inclusion relation betweenand,thenis a definable set,otherwise,is the degreekrough set.

§4.Neighborhood-based set-valued double-quantitative rough sets

Let(U,A,V,f)be a set-valued information system andB⊆A,Bis the fuzzy similarity relation ofB.0≤β＜α≤1 and 0≤k≤|U|,k∈R.For any(U),let

The logical operators are introduced into the upper and lower approximations,and four neighborhood-based double-quantitative rough approximations are obtained.There are two kinds of upper approximation operators,which can be shown as follows.

(1)The upper approximation operator with logical“and”The upper approximation operator with logical“and”also can be defined as

(2)The upper approximation operator with logical“or”.The upper approximation operator with logical“or”also can be defined as

There are two lower approximation operators,which are:

(1)The lower approximation operator with logical“and”,The lower approximation operator with logical“and”can also be defined as,

(2)The lower approximation operator with logical“or”,The lower approximation operator with logical“or”can also be defined as

Based on the above four approximation operators,optimistic and pessimistic doublequantitative rough set models are proposed here,the upper and lower approximations of neighborhood-based set-valued pessimistic double-quantitative rough sets model(NBSVP-DqRS)both choose the approximation operators with logical“and”,denoted by(U,;the upper and lower approximations of neighborhood-based setvalued optimistic double-quantitative rough sets model(NB-SVO-DqRS)both choose the approximation operators with logical“or”,denoted byDue to the introduction of different logical operators in the models,compared with the NB-SVO-DqRS model,the upper and lower approximation conditions of the NB-SVP-DqRS model are more stringent,therefore the classification conditions are also more stringent.The two models will be elaborated as follows.

Definition 4.1.Let(U,A,V,f)be a set-valued information system and BA,is the fuzzysimilarity relation,for any∈F(U),x∈U,the NB-SVP-DqRS model is defined as

The NB-SVP-DqRS model can also be defined as

Definition 4.2.Let(U,B,V,f)be a set-valued information,andis the fuzzy similarityrelation,the NB-SVP-DqRS model can be represented as(U,,Obviouslythere is no strict inclusion relationship between the upper and lower approximations of thismodel,so the positive domain,negative domain,upper boundary domain,lower boundary domain of NB-SVP-DqRS model are defined as:

Definition 4.3.Let(U,A,V,f)be a set-valued information system and B⊆A.is the fuzzy similarity relation of B,for any∈F(U),x∈U,the NB-SVO-DqRS model is defined as

The NB-SVO-DqRS model can also be defined as

Definition 4.4.Let(U,B,V,f)be a set-valued information system,is the fuzzy similarityrelation of attribute set B.Use(U,to represent the NB-SVO-DqRSmodel.The positive domain,negative domain,upper boundary domain,lower boundary domain of NB-SVO-DqRS model are defined as

In the above two models,if the objects belonging to the positive region,we make the decision to accept;if the objects belonging to the negative region,we make the decision to reject;if the objects belonging to the boundary region indicate that we need to make further judgments before we can make a decision.Among them,the objects in the upper boundary domain are more inclined to reject,and the objects in the lower boundary domain are more inclined to accept.

In the following,we will analyze the two NB-SV-DqRS models with practical examples to obtain the upper and lower approximations and to discuss the decision rules of two models respectively.

Example 4.1.Given a set-valued information system I=(U,A,V,F)(Table 1).The universe U is a universe of 6 products,five attributes a1,a2,a3,a4,a5,respectively represent the size,feel,weight,color,and shape of the product.Given a target set=represent each parameter of the product,set the parameterα=0.50,β=0.45,k=1.0.Then we can discuss how to make decisions based on the NB-SV-DqRSmodels.

Table 1 Set-valued information system

Calculate the distance between objects according to the distance function

It is easy to find that max(Dij)=1.92,then normalize the above matrix to

The fuzzy similarity matrix is

Then the fuzzy similarity classes of attribute setAcould be obtained as follows.

Consequently,

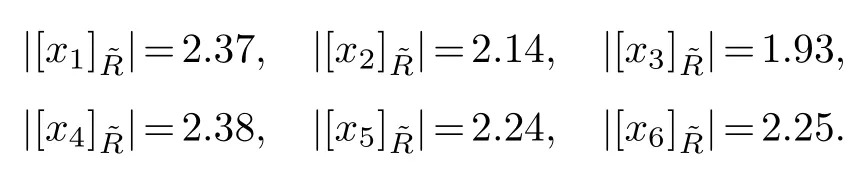
And the conditional probabilities of all objects are

Then the upper and lower approximations of the NB-SVP-DqRS model are expressed as

The corresponding positive region,negative region,upper boundary region,and lower boundary region are derived as follows,

The objectsx4,x5belonging to the positive region indicates that they are qualified;the objectsx1,x2,x3,x6belonging to the negative region indicates that their quality are unqualified;and the productx6belonging to the upper boundary region needs further inspection to determine whether it is qualified or unqualified,but it is more likely to be qualified;and here products belonging to the lower boundary domain don’t exist.

And the upper and lower approximations of the NB-SVO-DqRS model are expressed as

Its positive region,negative region,upper boundary region,and lower boundary region are as follows,

The productsx4,x5belonging to the positive region indicates that they are qualified;the productsx1,x2,x3,x6belonging to the negative region indicates that they are unqualified;and the productsx2,x3,x6belonging to the upper boundary region need further inspection to determine whether it is qualified or unqualified,but they are more likely to be qualified;at here no product belongs to the lower boundary region.

§5.Lower approximation reduction based on double-quantitative rough set

In the previous section,two double-quantitative rough set models under the set-value information system were constructed,and decision rules were obtained.In this section,the lower approximation reduction methods of the two models will be discussed.

Definition 5.1.Let(U,A,V,f)be a set-valued information system,R is a fuzzy similarity relationship based on this information system.Where BA is an approximate reduction in a set-valued information system,the following two conditions must be established:

(1)RB(X)=RA(X),

(2)For any b∈B,exist.

Definition 5.2.For a set-valued information system(U,A,V,f),its lower approximation reduction always exists.

For any a∈A,if both exist,thenAis a reduction.If a∈A,let,then researchB1=A-{a},for anyb1∈B1,there is,soB1is a reduction,if existb1∈B1,let,then researchB2=B1-{b1},and as so on.SinceAis a finite set,the setBcan always be found,letRB(X)=RA(X),at this time,Bis a reduction of the information system.

Recalling the previous section,two rough set models have been constructed in the set-valued information system,containing two lower approximation operators,namelyandThe reductions of two models are all keep the lower approximation constant.In the following part,we just take the lower approximation reduction algorithm of the NB-SVP-DqRS model as an example to illustrate the two lower approximation reduction algorithms.

Algorithm 1:Lower approximation reduction based on invariance ofimages/BZ_20_1031_1425_1054_1467.png∨(α,β,k)(~X)Input :A set-valued decision information system SDS(U,A∪D,V,f).Output:The reduction A.1 Step 1:Construct fuzzy similar relationimages/BZ_20_1031_1425_1054_1467.png and calculate theimages/BZ_20_1031_1425_1054_1467.png∧(α,β,k)(~X)of SDS.2 Step 2:A is the conditional attribute set,and only delete the attribute ai(ai∈A)every time on A,calculate theimages/BZ_20_1031_1425_1054_1467.png∧(α,β,k)(~X)of(U,A-{ai}∪D,V,f),and compare with step 1.3 Step 3:Ifimages/BZ_20_1031_1425_1054_1467.png∧(α,β,k)(~X)changes,add ai to the array B;ifimages/BZ_20_1031_1425_1054_1467.png∧(α,β,k)(~X)doesnt change,add ai to the array K,K is kernel element.Let i=i+1,determine whether there is an attribute ai in the set A that has not been deleted.If true,go to step 3;if false,go to step 5.4 Step 4:Follow a sequence to add the attributes aBi which stored in the set B to the kernel element set K,calculate theimages/BZ_20_1031_1425_1054_1467.png∧(α,β,k)(~X)of(U,K+{aBi}∪D,V,f),and compare with step 1,if the result is the same,stop adding aBi to K,if the result is different,adding aBi to K.5 Step 5:Return A.

The kernel idea of this algorithm is to obtain the non-kernel element setBat first,and then sequentially add the attributesaBiwhich is stored in the setBto the kernel attribute setK,aBi∈A-K,until theof(U,A∪D,V,f)is same as theof(U,A∪D,V,f).At this time,K+{aBi}is the reduction.The complexity analysis of algorithm 1 is conducted as follows.

Input a set-valued information system withm×ndimensions,the time complexity of algorithm step 1 isO(m2n2).The time complexity of calculating fuzzy similarity relationisO(mn2),the time complexity of calculatingisO(m),the purpose of algorithm steps 2 and 3 is to find the kernel elements,their time complexity areO(m),step 4 is to find the reduction,the best situation is that the setBis an empty set,and the kernel itself is a reduction,at this time the total time complexity isO(m2n2);the worst situation is that algorithm needs to judgem-itimes,at this time,the process of calculatingneeds to be loopedm-itimes,so at this time the total time complexity isO(m3n2).

The calculation idea of space complexity is similar to time complexity.In Step 1,only one array is needed in the construction of fuzzy similarity relationshipand the calculation of,their space complexity are bothO(1).The best situation is that the setBis an empty set,and the kernel itself is a reduction,at this time the total space complexity isO(1);the worst situation is that algorithm needs to judgem-itimes,at this time,the process of calculatingneeds to be loopedm-itimes,so at this time the total space complexity isO(m).

In summary,at the best of times,the total time complexity isO(m2n2),and the total space complexity isO(1);at the worst of times,the total time complexity isO(m3n2),and the total space complexity isO(m).

The reduction algorithm ideas of the optimistic double-quantitative models are roughly the same as the model based on theinvariant reduction algorithm.The difference is only that the function of the lower approximation operator is different.We Only need to be replace the lower approximation function in the above algorithm with optimistic double-quantitative model’s lower approximation function,so we will not go into details at here.

In the following,we will combine an example to reduce the attributes of the four rough set models proposed earlier in this paper,and explore the characteristics of each model.

Example 5.1.Given a target set-valued information system I=(U,A,V,D,F)(Table 2).The universe of discourse U={x1,x2,···,x9},the conditional attribute set A={a1,a2,···,a4},Let α=0.68,β=0.45,k=0.72.We want to find the reduction results of the four rough set models in the set-valued information system I.

Table 2 A decision set-valued information system

Since the method of computing the lower approximation is the same to Example 4.1,we will not go into details at here.According to the algorithm proposed,we separately calculate the reductions for four models and obtain the results in Table 3.

Table 3 Calculation results of the degree of change

According to the results,the lower approximation under the set-valued information system of these four models is{x2,x3,x4,x7,x8}or{x2,x4,x7,x8}.Though,those models which have same lower approximation results,their lower approximation reduction results are different,it is due to the different constraints of four models.Comparing the NB-SVP-SqRS model with the NB-SVD-SqRS model,the lower approximation and lower approximation reduction of these two models are both different.The reason is that although the two models have introduced quantitative information when they are constructed,the types of quantitative information are different,the constraints the models are classified are also different.When the model is classified,the former are focuses on relative quantitative information,while the latter are focuses more on absolute quantitative information.Then Comparing the NB-SVP-SqRS model with the NB-SVD-SqRS model,it is clear that the lower approximations of the two models are not the same but the attribute reduction results are the same,this is caused by the introduction of different logical operators in the two models.Compared with the optimistic double-quantitative model,the logical operators introduced by the pessimistic double-quantitative model make the lower approximation conditions of the model more stringent,so it has fewer elements,the lower approximation of optimistic double-quantitative rough set model is a subset of the pessimistic double-quantitative rough set model.Finally,compared with the NB-SVO-DqRS model and the NB-SVD-SqRS model,when the two models have the same lower approximation,but the reduction results are different.The reason is that,compared with the single-quantitative model,the constraint conditions of the approximation operators are increased in the double-quantitative model due to the introduction of logical operators,the requirements of the reduction are changed,and the reduction results will also be affected.

§6.Analysis on the advantages and disadvantages of quantitative rough set models

In order to clearly reflect the retention of the features contained in the original information system after the reduction of the four models,in this section,we use three data sets of different sizes as the background to calculate the lower approximation reduction results of the quantitative rough set models.Combining with the KNN algorithm,we can obtain the classification accuracy after reduction to reflect the classification ability of each model after reduction,and then we can compare the advantages and disadvantages of each model.Table 4 gives some basic information of the four experimental data tables.

Table 4 Basic information of the data sets

K nearest neighbor algorithm(K-Nearest neighbor,KNN)is one of the relatively simple and theoretically mature classification algorithms in machine learning.The basic idea is to first calculate the K neighbors in the training sample set which are closest to the sample to be classified.If most of the K neighbor samples belong to a certain category,then the sample also belongs to this category.Then we will use the idea of KNN algorithm and replace the distance function of the traditional KNN classifier with the distance function constructed in Section 2.Based on the traditional KNN classifier,we redefine the applicable KNN classifier under the set-valued information system,short as KNN-SVIS.The data set is divided into training set and test set according to the ratio of 7:3.We calculate the lower approximation reduction of four models under each data set,then use the KNN-SVIS classifier to calculate the accuracy.The calculation results are shown in the following Table 5.

Table 5 Calculation results of accuracy rate

It can be seen from the calculation results shown in Table 5 that the performance of the four models is different under different data sets.In the first information system,the NB-SVP-SqRS model and NB-SVP-DqRS performed better,while the classification accuracy rate of the NB-SVD-SqRS model reduction is significantly lower.In the second information system,the NB-SVD-SqRS model and the NB-SVO-DqRS model performed better.In the third information system,the NB-SVP-SqRS model and NB-SVP-DqRS model perform better.Due to the different restriction conditions of the four models,the applicable models are different.NB-SVP-SqRS model and NB-SVP-DqRS model are more suitable for data sets”segmentation”and”HCV”,while NB-SVD-SqRS model and the NB-SVO-DqRS model are more suitable for the data set”audit”.By comparing the four models horizontally,the reduction results of the NB-SVP-SqRS model and the NB-SVP-DqRS model have higher classification accuracy than the NB-SVD-SqRS model and the NB-SVO-DqRS model under these three data sets,they have stronger ability to retain the characteristics of the original information system.

Fig.1 The classification accuracy for different data sets.

It is clear from Figure 1 that except for the data set”audit”,the classification accuracy rates of the other two data sets are unsatisfactory,the classification accuracy rates of these four models on the data sets”segmentation”and”HCV”are all lower than 30%.If only judge the model from the calculation results of the accuracy rate,these four models are not suitable for knowledge mining on the data sets”segmentation”and”HCV”,but such conclusions are obviously one-sided,because the KNN-SVIS model has model errors,even the original attribute set is not 100% accuracy when using the KNN-SVIS model for classification prediction,the classification accuracy of the reduction result will also be affected by the model error.If only the size of the accuracy rate calculation result is considered,it cannot truly reflect the feature retention of the original information system by the attribute reduction result of the model.

In order to eliminate the influence of the KNN model error and truly reflect the change of the information contained in the reduction result compared with the original information system,the concept of the degree of change is proposed here.

Suppose PAis the accuracy rate of the original attribute set after KNN-SVIS model reconstruction,and Pais the accuracy rate of a model reduction result after KNN-SVIS model reconstruction,then define the degree of change,.

Obviously,D∈(-1,1),the smallerDindicates that the reduction result retains the fewer features of the original information system.

According to the above formula,the degree of change of the four models under the three data sets are calculated respectively.The calculation results are shown in Table 6.

It can be seen from Table 6 that in the first information system,the attribute reduction results of the NB-SVP-DqRS model and the NB-SVP-SqRS model are better to retain the characteristics of the original information system,compared with the original information system,in those model,only about 15% of the features are lost,while the reduction results of the NB-SVD-SqRS model and the NB-SVO-DqRS model respectively lose about 42% and 53%of the features.In the second information system,the degree of changeDof the NB-SVD-SqRS model and the NB-SVO-DqRS model are both greater than 0,it indicates that the attribute reduction can more accurately describe the characteristics of the information system than the original attribute set,compared with the original information system,the characteristics of the information system contained in the reduction results of the NB-SVP-DqRS model and the NBSVP-SqRS model remain unchanged.In the third information system,the attribute reduction results of the NB-SVD-SqRS model and the NB-SVO-DqRS model retain the characteristics of the original information system poorly,compared with the original information system that only lost about 11% of the features,the reduction results of the NB-SVP-DqRS model and the NB-SVP-SqRS model did not change the features of the information system contained in the original information system.

Data set Model Degree of change NB-SVP-SqRS -0.1589 NB-SVD-SqRS -0.4205 NB-SVO-DqRS -0.5265 segmentation NB-SVP-DqRS -0.1589 NB-SVP-SqRS 0 NB-SVD-SqRS 0.042 NB-SVO-DqRS 0.042 audit NB-SVP-DqRS 0 NB-SVP-SqRS 0 NB-SVD-SqRS -0.1065 NB-SVO-DqRS -0.1065 HCV NB-SVP-DqRS 0

Fig.2 The degree of change under different data sets.

It shows that these three information systems can all use the above rough set model for knowledge mining,but due to the differences between different information systems,different rough set models are applicable to different information systems.The data set segmentation and HCV are more suitable to use NB-SVP-DqRS model and NB-SVP-SqRS model for knowledge mining,and as to the data set audit,NB-SVD-SqRS model and NB-SVO-DqRS model are more suitable.

In a word,for different information systems,the NB-SV-SqRS model and the NB-SVDqRS model show different advantages.Due to the different restriction conditions of the lower approximation,the reductions of these four models also show different characteristics.When processing data,we can choose the model according to actual needs.

§7.Concluding remarks

This paper proposes single-quantitative rough set models and double-quantitative rough set models in the set-valued information system,and the related lower approximation reduction algorithms for neighborhood-based set-valued double-quantitative rough set model are also provided.Moreover,respective calculate the lower approximation reduction of probability single-quantitative,degree single-quantitative,optimistic double-quantitative and pessimistic double-quantitative rough set models are discussed based on the proposed quantitative rough set models,and then the lower approximation reduction algorithms are carefully investigated.Finally,the KNN algorithm was applied to evaluate the accuracy of the classification of the proposed models after lower approximation reduction.In the future work,we will focus on our model as a classifier,and compare it with other existing classical classifiers to obtain its classification effect.