软弱下卧层压缩模量对基础沉降控制分析
2021-07-05殷诗茜范柱国曾营
殷诗茜,范柱国,曾营
(昆明理工大学国土资源工程学院,昆明 650093)
1 前言
在地基基础设计时,基础荷载直接作用的土层叫持力层,持力层承受的荷载随土体深度越来越深而逐渐减小到忽略不计,这层向下的土体就称为下卧层。下卧层虽然承受的荷载可以忽略不计,但如果出现软弱下卧层的情况,就必须考虑地基基础的沉降,控制其变形。其中地基土的压缩模量的取值直接影响着地基的变形(图1)。本文针对地基基础下卧层的性质与地基沉降关系进行研究,通过模拟出土层最佳压缩模量取值范围,并分析地基土软弱下卧层控制基础变形的因素,从而使地基基础的设计方案更加合理科学,不仅使能避免今后发生严重的工程事故,也能达到更好的经济效益。

图1 地基基础示意图
2 研究背景
在岩土工程中地基变形是工程师应该重点演算的部分,因为如果地基变形量过大,将会影响建筑物的正常使用,甚至是危害建筑物的安全。地基承载力不足以支撑上覆荷载和地基岩体被压缩导致变形是引起地基变形的这两个原因。
关于基础的沉降计算,现行普遍采用国家规范的半理论半经验的分层总和法(图2)。

图2 基础沉降计算的分层示意
在现行参考规范《建筑地基基础设计规范》(GB 50007-2002)[2]计算地基变形时,地基的最终变形量S(mm)的计算公式为:
(1)
这个方法需要使用的参数相对较少,参数获得途径容易,且计算数与实际数的准确度较高,所以多被普遍运用于工程。根据公式(1),在确定沉降经验系数、基础尺寸、基础底面处的附加应力以及各土层的压缩模量的情况下,能求出最终沉降量。
对于复合地基工程一般采用复合模量法,使用这个方法时,复合土层分层与天然地基相同,加固区和下卧层土体内的应力分布采用各向同性均质的直线变形理论[3]。 复合地基最终变形量S的计算公式为:
(2)
该方法适用于复合地基工程,相比于公式(1),多考虑了加固区土的模量提高系数,针对于复合地基计算更加接近实际。
无论哪种方法,土的压缩模量对两种计算沉降量的方法都有很大的影响。土的压缩模量是计算地基变形的一个重要指标,同时也是进行地基和建筑物沉降计算时需要确定的一个重要土性参数[4-5]。压缩模量用符号Es表示,老标准中按下式计算:
(3)
式中,ei为土体在自重压力作用下的天然孔隙比;a为土体从自重压力到自重压力与附加应力之和压力段的压缩系数。
压缩模量Es和压缩系数a都用于评价土的压缩性,压缩模量Es与土的压缩性呈反比。
关于沉降因素的讨论,赵幸[6]、庄铃强[7]等早就做了一系列研究证明影响地基沉降的因素有很多,包括上覆荷载、压缩模量、置换率、桩土应力比、地下水水位、降水量等等。本文选取部分影响基础沉降的因素进行多元线性回归分析。由于地基土的性质十分复杂,压缩模量的计算需要土体在完全侧限条件下进行,随着荷载的不断变化压缩模量也会不断变化,计算沉降也需要对压缩模量有一个正确估算。
3 实验模拟
在地基由多层土组成时,持力层以下存在容许承载力小于持力层容许承载力的土层时,这样的土层称之为软弱下卧层。为了研究软弱下卧层的最佳状态,通常会提出很多的猜想和物理模型。但下卧层力学性质复杂,想要构建物理模型十分困难,因此用数值模拟分析的方法更为高效。其中有限元法作为数值模拟分析的一个重要特点就是用结点上的函数值用来将区域内的函数近似的描述。有限元模拟方法的应用对研究地基沉降的特性、计算应力应变有较大地辅助作用,为合理的计算压缩模量提供了有效的手段。
因为地基的沉降是受多种因素共同作用生成的结果,为了能够准确分析出下卧层性质对于沉降的影响,这里采用有限元数值模拟的方法做了以下3个实验来得到一个最佳压缩模量反映下卧层的一个最佳状态。
3.1 选择土体本构模型
Mohr-Coulomb塑性模型主要适用于在单调载荷下颗粒状材料,在岩土工程中应用非常广泛。本文将采用Mohr-Coulomb模型作为土体本构模型,可应用于地基的极限承载能力的计算,以及其它以土体破坏为关键因素的计算。这个模型的优势在于计算参数少,便于获取,模型概念简单但能很好的反应出土体摩擦性材料的特性质,从而在岩土工程中被工程师们广泛运用。
ABAQUS软件中摩尔库伦模型需与线弹性模型联合使用,采用各向同性弹性模型,涉及参数弹性模量E与泊松比v,其可以随温度与其他场变量变化。但现有地勘报告中基本不涉及弹性模量参数,一般只提供一个Es。查阅文献,其中高大钊等编著《土质学与土力学》[8]一书中定义弹性模量一般为压缩模量的3~5倍。杨敏和赵锡宏根据60余根桩在工作荷载下的试验结果,反算了土的弹性模量E和压缩模量Es的比例关系,得出E=(2.5~3.5)Es[9]。因此,本文采用E=3*Es进行土体模拟分析,将实验数据中的压缩模量换算成弹性模量进行试验。
3.2 模型合理性的验证
为验证本文借助ABA QU S软件建立出的计算模型和参数选取的合理可靠,同时因为天然地基的浅基础具有省材料、易施工、造价低廉的优点,比深基础更加优先考虑。
这里采取了保山市某项目具体数据进行验算,土层信息详见表1,拟建建筑采用基础类型为浅基础,基础埋深为2.0 m。

表1 土体计算参数
如图3所示,通过模拟得出的p-s曲线与实际载荷试验的p-s曲线在各点处都能较好吻合,所以误差较小。因此,本文借助ABAQUS建立的计算模型和参数选取合理,可以使用该模型进行下一步的研究。
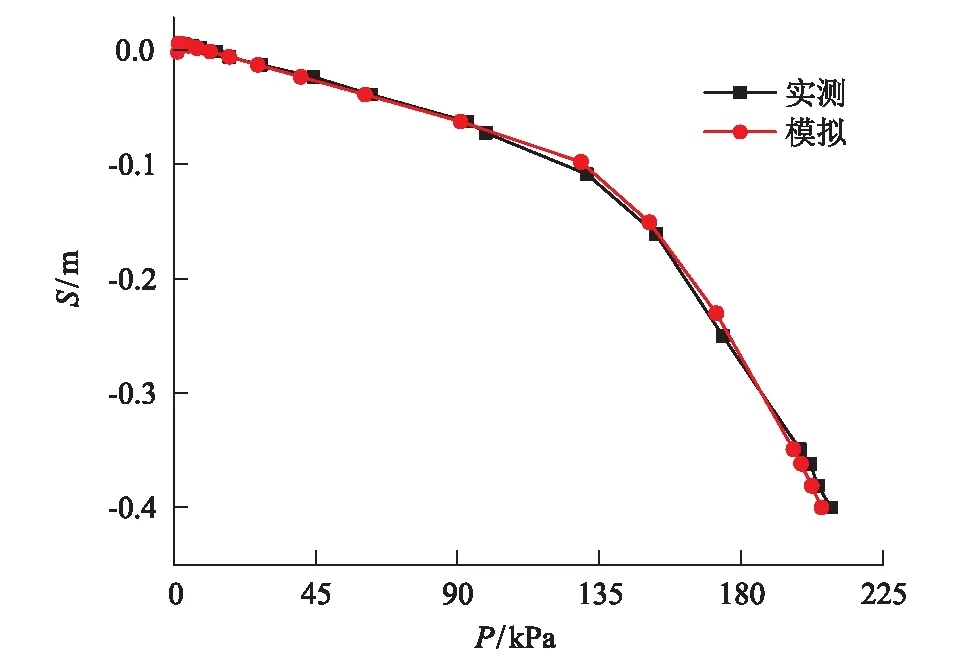
图3 模拟计算与实测数据对比
本文意在研究下卧层和沉降的关系。沉降量作为地基变形的表现形式,解决地基沉降的问题对于地基变形情况也有重要意义。
3.3 建立数值模拟模型
本文的研究模拟对象选取为浅基础-条形基础,在数值模拟中假设将实际工程采用平面有限元应变分析。为研究下卧层与沉降的关系,本文设计了3个数值模拟实验进行探究。
3.3.1 实验一
求持力层厚度与下卧层厚度的比值,为了避免出现因为地基持力层未发挥最佳承载力状态,而对研究地基变形实验产生影响的情况。
试验模型一:设置条形基础为宽度B=2 m,埋深D=1 m。则设计不同持力层厚度与下卧层厚度进行比值。设计持力层厚度为H分别为1.0 m(0.5B)、2.0 m(1B)、3.0 m(1.5B)、4.0 m(2B)、5.0 m(2.5B)、6.0 m(3B)、7.0 m(3.5B)、8.0 m(4B)、9.0 m(4.5B)、10.0 m(5B),共10组试验,编号分别为H1~H10。实验一参数详见表2。

表2 实验一参数表
图4为H1~H10荷载沉降p-s曲线,取p-s曲线上斜率发生显著变化的点所对应的荷载,为持力层的极限承载力,可得地基的极限承载力Pu随持力层厚度H增加的变化规律。图5为实验一的各组Pu曲线图,随持力层逐渐增加而下卧 层的厚度逐渐减小,各组Pu曲线斜率起始大、然后逐 渐 变小,发现持力层和下卧层厚度可以通过实验取到一个中间比值。曲线 拐 点大 约 在H5处,这时持力层和下卧层厚度比值为3得出实验一结果。

图4 H1~H10荷载沉降p-s曲线

图5 实验一 各组Pu曲线图
3.3.2 实验二
实验二是在最佳厚度比的计算结果下,判断最佳压缩模量比值。通常在对软弱下卧层顶面处的附加压力pz进行计算的时候会使用到国内外通用的扩散角法。地基压力扩散角θ是地基压力扩散线与竖直线的夹角[4],上层土的压缩模量Es1和下层土的压缩模量Es2影响着地基压力扩散角θ的取值。因此上层土的压缩模量Es1和下层土的压缩模量Es2的关系直接影响到地基的基础承载力,研究Es1/Es2是很有必要的。
试验模型二:基于上述实验找出的下卧层与持力层最佳厚度比,设置条形基础为宽度B=2 m,埋深D=1 m。保持相同的持力层压缩模量与不同的下卧层压缩模量进行比值,共10组试验,编号分别为H11~H20。实验二参数详见表3。

表3 实验二参数表
图6为H11~H20荷 载沉降p-s曲线,由图可知p-s曲线的变化规律。取p-s曲线上斜率发生显 著变化的点所对应的荷载,规律也和实验一相同。图7为实验二的各组Pu曲线图,随下卧 层厚度压缩模量Es2的增加,各组Pu曲线斜率起始大、然后逐 渐 变小,说明下卧层压缩模量等量增加时,在Es2较小时,下卧层压缩模量对地基承载力影响相对较大,后随着Es2的增大影响反而 逐渐 减小。曲线 拐 点大 约 在H15处,这时E1/E2的比值为0.25。这时的扩散角为最佳扩散角。所以得出了实验二想要求取的最佳压缩模量比值为0.25。

图6 H11~H20荷载沉降p-s曲线
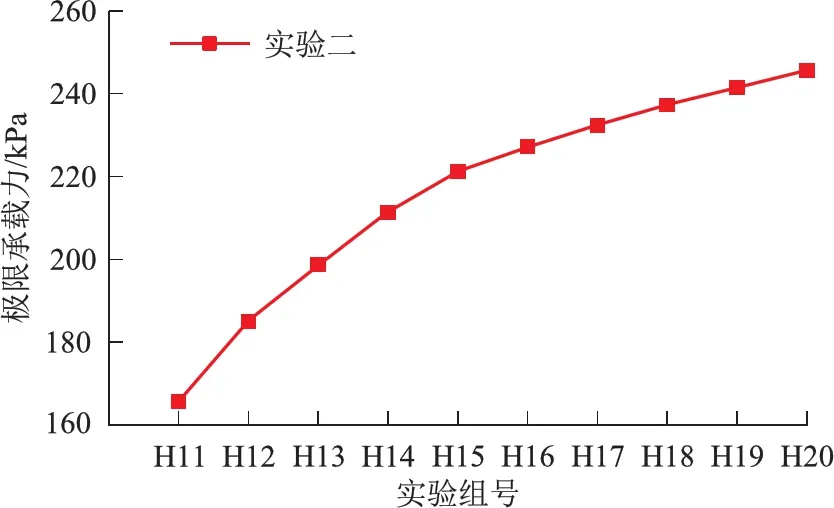
图7 实验二各组Pu曲线图
3.3.3 实验三
在得到最佳压缩模量比值后,为找出一个最佳下卧层压缩模量值范围,设计实验三实验。
试验模型三:条形基础为宽度B=2 m,埋深D=1 m。保持下卧层与持力层的比值为0.25时,改变持力层与下卧层的压缩模量值,共10组试验,编号分别为H21~H30。实验三参数详见表4。

表4 实验三参数表

图8为H21~H30荷载沉降p-s曲线,此实验控制了Es2/Es1比值在实验二得出的最佳比值0.25的条件下进行。图9为实验三的各组Pu曲线图。实验三基于实验一的持力层最佳效果和实验二的最佳扩散角的情况下,扩散角相同,随压缩模量的增加,各组Pu曲线斜率起始大,然后逐渐变小,说明压缩模量呈比例增加时,在E较小时,压缩模量对地基承载力影响相对较大,而后反而逐渐减小。曲线拐点大约在H25处,持力层压缩模量为25,下卧层压缩模量为6.25。

图8 H21~H30荷载沉降p-s曲线
4 沉降量与控制因素相关性分析
基于前文的3个实验所得数据基础上更加深入研究沉降量与各变形控制因素相关性,主要研究因素包括上覆荷载、持力层压缩模量Es1、下卧层压缩模量Es2。
4.1 实验数据基本特征
本文选取的指标包括:选取沉降量S为因变量,选取上覆荷载P、持力层压缩模量Es1、下卧层压缩模量Es2为基本变量。本次研究的实验数据均来自前文3个实验所得出的实验数据,共整理有效数据532组。具体数据统计表见表5。

表5 基本物理指标和力学指标统计表
4.2 沉降量与变形影响因素相关分析
为了进一步研究沉降量S与软弱下卧层基础沉降变形影响因素的相关性[10],将上述实验数据应用SPSS软件进行多元线性回归统计分析,用于深入研究下卧层中影响沉降量的因素,并获得经验公式。回归统计结果如表6所示。

表6 沉降量与各物理指标相关分析表
结果显示,发现沉降量与各单一的物理指标相关性均不显著,最好的为多因素模型三。所以沉降量并非由单一物理因素所能决定,而是由多因素共同影响的。
沉降量S与上覆荷载F、持力层压缩模量Es1、下卧层压缩模量Es2有较好的多元线性相关关系,相关模型关系式分别为:
模型1:f(s)=-2.943+0.082F
模型2:f(s)=2.736+0.096Es1-0.26F
模型3:f(s)=2.714+0.097F-0.193Es1
-0.127Es2
由上述3类模型可以看出,论单因素的话,上覆荷载对沉降量存在较大的影响,两者呈正相关关系,上覆荷载越大沉降量就越大。3个回归模型的回归系数R2随着物理指标的增加而增加,说明上覆荷载F、持力层压缩模量Es1、下卧层压缩模量Es2均是决定沉降量的重要因子。模型三的相关系数最高,为0.705,因而推荐因素全面的模型三为经验公式。
5 结论
(1) 当基础埋深D相同,在改变持力层与下卧层的厚度,在下卧层与持力层厚度比值为3时,地基承载力发挥效能最佳。
(2) 基于地基在最佳厚度比的情况下,改变下卧层与持力层的压缩模量比值。在Es2/Es1的比值为0.25。此时的扩散角为最佳扩散角。
(3) 基于最佳扩散角与厚度比的情况下,压缩模量的改变,也直接影响着地基极限承载力。当到达一定的区间时,随着压缩模量的增大,地基承载力的提升效果减弱,拐点在Es1=25和Es2=6.25处。
(4) 基于SPSS对于有效数据532组进行多元回归线性分析。说明沉降量S与重要因子上覆荷载F、持力层压缩模量Es1、下卧层压缩模量Es2有着较好的多元相关线性关系。由模型三可得上覆荷载越大,沉降量越大。压缩模量越大,越不容易沉降。持力层压缩模量变化效益大于下卧层。
