基于ABAQUS研究持力层厚度对浅地基承载力的影响

曾营，徐世光,2，殷诗茜, 谢志鹏

(1.昆明理工大学国土资源工程学院，昆明 650093；2. 云南地矿工程勘察集团公司，昆明 650041)

1 研究背景及意义

俗话说：万丈高楼平地起。地基和基础是建筑物的根基，地基的选择和处理、基础的设计和质量的好坏直接影响到建筑物的可靠性、经济性。从可靠性出发，地基与基础的可靠性直接影响着建筑物的安全，如果发生地基或基础的破坏，其补救和处理十分棘手。从经济性出发，基础工程的造价费用占整个建设费用相当大的比例，一般情况下，采用浅基础的多层建筑的基础造价占建筑造价的15%～20%，采用深基础的高层建筑的基础工程造价占总建筑费用的20%～30%。

浅基础一般指基础埋深3～5 m，或者基础埋深小于基础宽度的基础，且只需排水、挖槽等普通施工即可建造的基础，如图1。

图1 浅基础示意图

因为浅基础的广泛应用与地基基础破坏事故的频发性与严重性，因此需要对浅基础机理和地基破坏规律进行研究、归纳与总结。在过去的时间里，国内外众多学者对浅基础地基土的破坏机理、建立及修正地基极限承载力理论公式、地基承载力确定方法等等方面的探索取得了卓越的成效[1]。马少坤等[2]应用在基础上方模拟增量加载的方式，再现了地基极限破坏状态，分析了均质无重度地基的的极限承载力。张中辉[3]从地基土参数、基础埋深、地基土空洞缺陷3个方面入手，采用数值模拟方法，研究了不同因素对浅基础地基破坏。高广运等[4]利用有限差分程序建立三维非线性有限差分数值模型，研究了持力层性质对大直径扩底桩竖向承载性状的影响。

本文针对浅基础持力层厚度变化导致影响地基承载力的研究，以期更好的认识持力层厚度的重要性，与掌握地基的承载力发挥规律；更科学合理的选择浅基础方案，不仅使能避免今后发生严重的工程事故，也能达到更好的经济效益。

2 浅地基极限承载力

地基承载力是岩土工程的三大经典土力学问题之一[5]，满足承载力要求作为选择浅基础方案的基本要求。确定地基承载力的检测方法有原位实验法、规范表格法、理论公式法、当地经验法，本文采用有限元数值模拟方法，计算求出地基极限承载力，并得到持力层对浅地基承载力的影响规律。

2.1 浅基础的破坏模式

在上覆荷载的作用下，地基因为没有足够的承载能力而引起破坏，一般都由地基土的剪切破坏引起。现有的研究表明，浅基础的地基破坏模式有3种：整体剪切破坏、局部剪切破坏和冲切剪切破坏[6]。

该3种破坏模式主要根据载荷试验和实际工程破坏由前人提出的概念，在现场载荷试验中可以得到各级荷载及其相应的相对稳定沉降值，可得到荷载和沉降的关系曲线，即p-s曲线。

最早提出整体剪切破坏的概念是L.普朗德尔在1920年提出，这是一种在浅基础荷载作用下地基发生连续剪切滑动面的地基破坏模式；最早提出局部剪切破坏的概念是K.太沙基于1943年提出，这是一种在浅基础荷载作用下地基某一范围内发生剪切破坏区的地基破坏模式；最早提出冲切剪切破坏的概念是E.E.德贝尔和A.S.魏锡克在1959年提出，这是一种在浅基础荷载作用下基础产生较大沉降、地基土体发生垂直剪切破坏的地基破坏模式[3]。地基破坏示意图见图2所示，p-s曲线如图3。

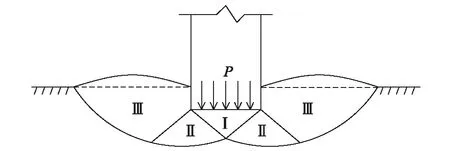
图2 地基破坏示意图

图3 地基破坏p-s曲线

2.2 理论计算确定地基极限承载力

目前求解地基极限承载力的主要理论公式有[7-9]：

(1) 普朗德尔(Prandtl)极限承载力理论在1920年提出，该理论假设基础具有无限刚度，且接触光滑，置于介质表面，地基是无重度的刚塑性材料。

其计算公式为：

pu=c·cotφ[exp(πtanφ)tan2((45°+φ/2)-1)]

+q·exp(πtanφ)tan2((45°+φ/2)

(1)

(2) 太沙基(Terzaghi)极限承载力在1943年提出，在普朗德尔的基本理论基础上，提出了考虑基础下土自重的极限承载力公式，基础底面以上地基土以均布荷载q=γod代替，即不考虑基础两侧土体抗剪强度的影响。从而发展出太沙基承载力理论。

其计算公式为：

pu=cNc+qNq+1/2γbNr

(2)

Nc=(Nq-1)cotφ

(3)

Nq=exp[(3π/2-φ)]/2cos2(45°+φ/2)

(4)

Nr=[(KPr/2cos2φ)-1]tanφ/2

(5)

式中Nc、Nq、Nr为粗糙基底的承载力系数;φ是内摩擦角的函数;KPr为被动土压力系数。

(3) 迈耶霍夫(Meyerhof)极限承载力在1951年提出，其在改进太沙基极限承载力公式中，不考虑基础两侧土体抗剪强度的影响。该理论提出了考虑地基土塑性平衡 区随着基础埋置深度的不同而扩展到最大可能的到达程度，并且也要计算基础两侧土体抗剪强度对承载力影响的地基承载力计算方法[3]。

其计算公式为：

pu=cNc+qNq+1/2γbNr+2fd/b

(6)

式中,Nc、Nq、Nr为粗糙基底的承载力系数；γ是内摩擦角φ的函数；f为土与基础侧面单位面积的摩擦力；d为基础埋深；b为基础宽度。

(4) 汉森(Hansen)极限承载力在1970年提出，在前人的基础上，多考虑了基础形状、荷载倾斜与偏心、地面倾斜的影响因素。

其计算公式为：

pu=cNcScicdcgcbc+qNqSqiqdqgqbq

+(1/2)γbNrSrirdrgrbr

(7)

式中,Nc、Nq、Nr为粗糙基底的承载力系数；Sc、Sq、Sr为基础形状修正系数；ic、iq、ir为荷载倾斜修正系数；dc、dq、dr为基础埋深修正系数；gc、gq、gr为地面倾斜修正系数；bc、bq、br为基底倾斜修正系数。

以上理论方法求解时，均需假定滑裂面的形状，土体材料假设为刚塑性材料。没充分考虑地基土体的真实应力应变关系和基础刚度以及基底接触面粗糙程度等因素的影响，无法全面地反映地基破坏的过程，计算求出的极限承载力Pu与实测Pu会存在一定偏差，具有局限性。

2.3 浅基础破坏的影响因素

由于地基土是自然体，其影响变量众多。影响地基破坏的因素主要有地基土的条件和基础条件，其中地基土的条件包括地基土的种类、密度、粘聚力、压缩性和内摩擦角等；基础条件包括基础的型式、埋深、尺寸等[6]。并且根据“2.2节”理论计算确定地基极限承载力中，理论公式的计算，可得出主要影响因素为：粘聚力c、内摩擦角φ、荷载q、基础埋深d、基础宽度b。

3 浅基础极限承载力模拟分析

岩土材料复杂的性质，构建模型难度大，所以数值模拟分析得到的结果常常受到参数选择、边界条件、本构模型的选择等很多因素的影响，因此结果要与试验结果进行检验对比，方可确认结果的合理及准确性。有限元模拟方法的应用对研究岩土体材料的特性、计算应力应变有较大地推动作用，为合理计算地基承载力提供了有效的手段。

根据上文可知，浅基础的地基破坏是受到多种因素的影响，但由于为了准确的分析出地基持力层厚度对地基承载能力的影响，因此采用有限元数值模拟的方法，对地基持力层厚度进行了变量分析。

3.1 ABAQUS在岩土工程中的应用

岩土工程分析中，由于岩土体应力应变关系的非线性、荷载及边界条件的复杂性，用解析方法求解难度很大，通常需采用数值方法进行求解，数值分析结果是岩土工程师对问题进行判断的重要依据之一，ABAQUS是一款功能强大的通用有限元软件，包含十分丰富的材料模型、单元模式、荷载及边界条件，能够求解静力、动力等多种问题，尤其在求解非线性问题方面的能力十分优异，对岩土工程有较好的适用性[10]。

3.2 土体本构模型的选择

Mohr-Coulomb屈服准则为描述岩土工程材料最常用的准则，摩尔-库伦定理是土力学的经典定理，一个基于工程常用土体参数的弹塑性土体本构模型。因为该模型参数少，容易获得，概念简单而又能反应土体的摩擦性材料的特性深受工程师们的喜爱。可应用于地基的极限承载能力的计算，以及其它以土体破坏为关键因素的计算。

3.3 模型验证

为验证本文借助ABAQUS建立的计算模型和参数选取合理可靠，采取曲靖市某项目具体数据进行计算，土层信息见表1，拟建建筑采用基础类型为浅基础，基础埋深1.50 m。

表1 土体计算参数

如图4所示，模拟计算得出的p-s曲线与实际载荷试验p-s曲线在各点处，吻合较好，误差较小。因此，本文借助ABAQUS建立的计算模型和参数选取合理，可使用该模型，进行进一步深入研究。

图4 模拟计算与实测数据对比

3.4 数值模拟模型建立

本文所研究的持力层厚度影响针对浅基础——条形基础，在数值模拟中可以将实际工程采用平面有限元应变分析。为研究持力层厚度对地基承载能力的影响，设计以下数值模拟试验。

试验模型一：条形基础为宽度B=2 m，埋深D=1 m。则设计持力层厚度为H分别为1.0 m(0.5B)、2.0 m(1B)、3.0 m(1.5B)、4.0 m(2B)、5.0 m(2.5B)、6.0 m(3B)、7.0 m(3.5B)、8.0 m(4B)、9.0 m(4.5B)、10.0 m(5B)共10组试验，编号分别为H1～H10。

试验模型二：条形基础为宽度B=2 m，埋深D=2 m。则设计持力层厚度为H分别为1.0 m(0.5D)、2.0 m(1D)、3.0 m(1.5D)、4. 0 m(2D)、5.0 m(2.5D)、6.0 m(3D)、7.0 m(3.5D)、8.0 m(4D)、9.0 m(4.5D)、10.0 m(5D)共10组试验，编号分别为H11～H20。

两个试验中，地基土体均设置为均匀，可用Mohr-Coulomb模型进行模拟。土体参数见表2。

表2 土体计算参数

试验模型三：条形基础为宽度B=2 m，埋深D=1 m。改变土体粘聚力参数c2=2c1，土体参数见表3。则设计持力层厚度为H分别为1.0 m(0.5B)、2.0 m(1B)、3.0 m(1.5B)、4.0 m(2B)、5.0 m(2.5B)、6.0 m(3B)、7.0 m(3.5B)、8.0 m(4B)、9.0 m(4.5B)、10.0 m(5B)共10组试验，编号分别为H21～H30。

表3 土体计算参数

试验模型四：条形基础为宽度B=2 m，埋深D=1 m。改变土体内摩擦角参数φ3=2φ1，土体参数见表4。则设计持力层厚度为H分别为1.0 m(0.5B)、2.0 m(1B)、3.0 m(1.5B)、4.0 m(2B)、5.0 m(2.5B)、6.0 m(3B)、7.0 m(3.5B)、8.0 m(4B)、9.0 m(4.5B)、10.0 m(5B)共10组试验，编号分别为H31～H40。

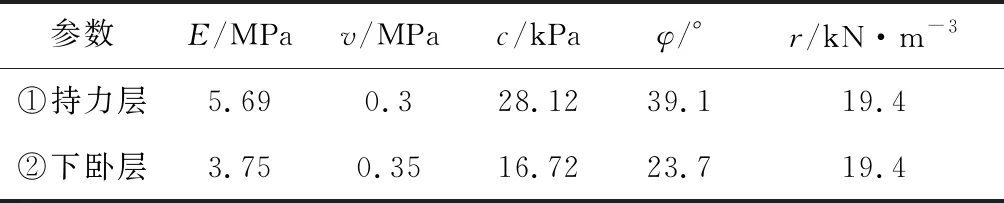
表4 土体计算参数

整个模型高度为20 m，宽度100 m，整体尺寸满足浅基础往两侧与下部影响范围。数值模拟加载时，均在基础顶部每级按100 kN加载。模型图如图5、图6。

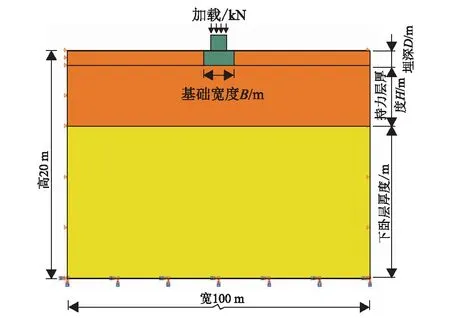
图5 计算模型示意图

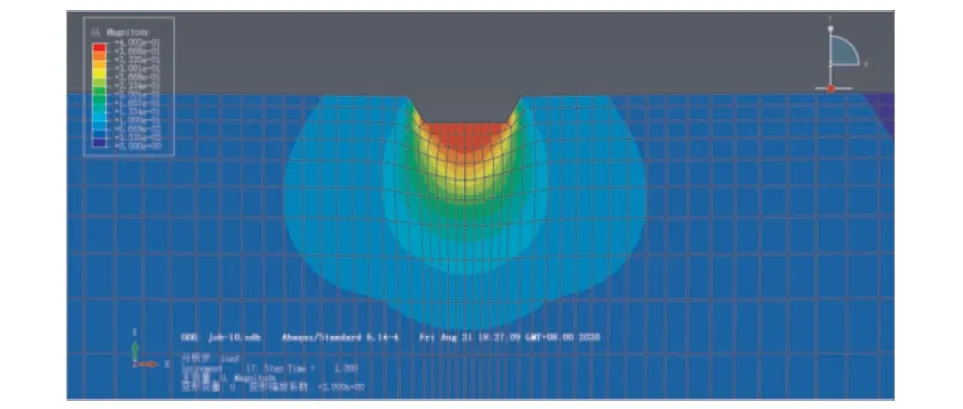
图6 加载位移变形图

4 计算结果分析

4.1 基础埋深与持力层厚度的关系

图7为H1～H10荷载沉降p-s曲线，图8为H11～H20 荷载沉降p-s曲线，由图可知，他们的p-s曲线具有相同的变化规律。取p-s曲线上斜率发生显著变化的点所对应的荷载，为持力层的极限承载力，可得地基的极限承载力Pu随持力层厚度H增加的变化规律，如图9所示。由图9可知，实验一、实验二两组曲线具有相同的变化规律，当两者持力层厚度一致时，其Pu值大致一致，说明基础埋深D的增加，对地基土竖向应力分布规律影响较小。

图7 H1～H10荷载沉降p-s曲线

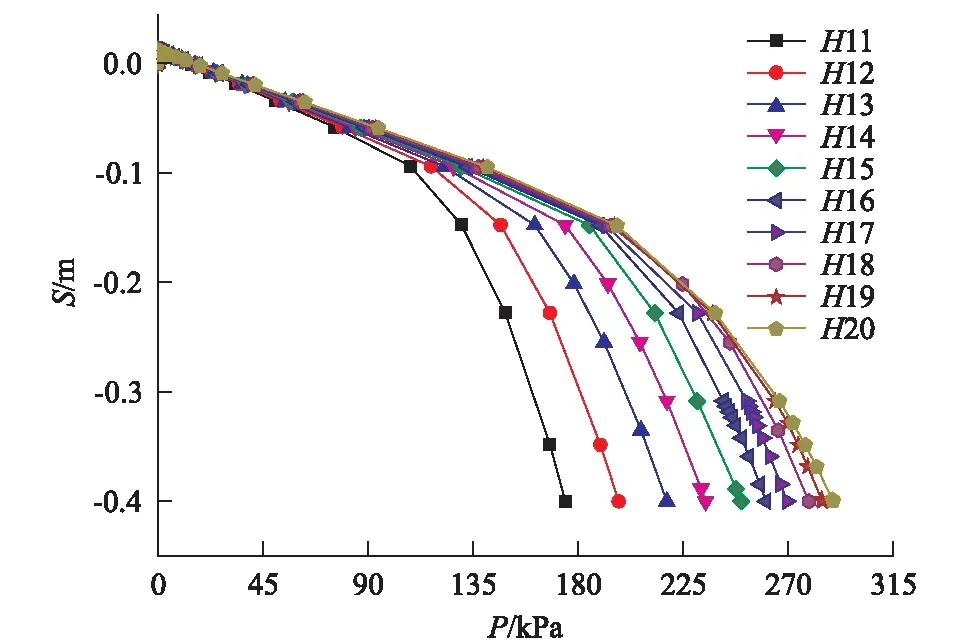
图8 H11～H20荷载沉降p-s曲线

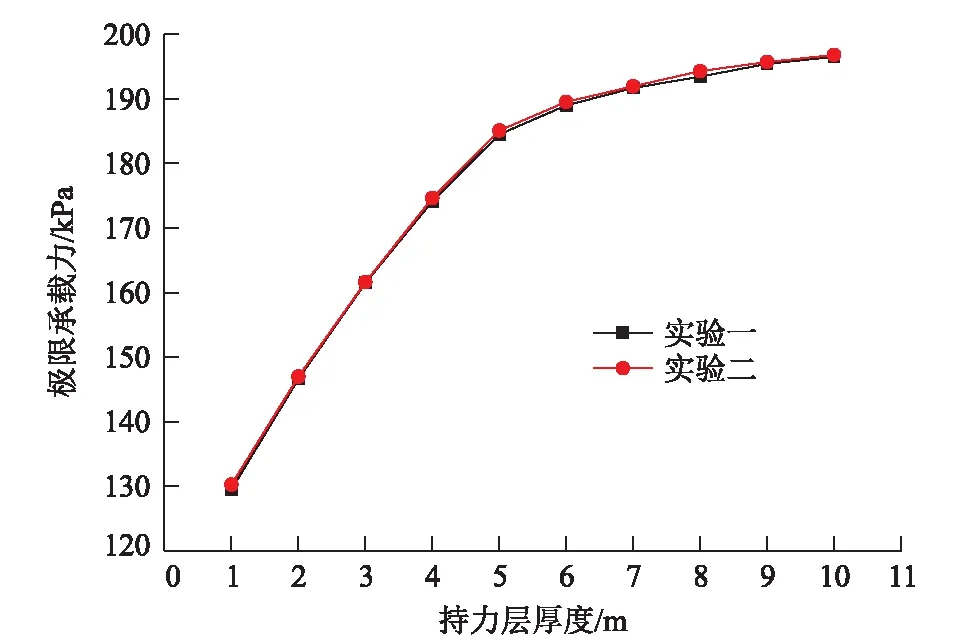
图9 实验一、二H～Pu曲线对比图

随持力层厚度H的增加，H-Pu曲线斜率起始大、然后逐渐变小，说明增加相同的持力层厚度，在持力层厚度较小时，持力层厚度对地基承载力影响相对较大，随着持力层厚度的增大影响逐渐减小。曲线拐点大约在H=5 m处，即H/B=2.5与H/D=2.5处，因此，在实际的浅基础工程设计中，尽量使得持力层厚度大于2.5B(D)时，能减小持力层厚度变化对地基承载力的影响。

4.2 粘聚力与持力层厚度的关系

地基土的c体现的便是土体抗剪度的强弱，图10为H21～H30荷载沉降p-s曲线，由图可看出其与基础埋深对p-s曲线的影响机理一致。由图11可知，实验一、实验三两组H-Pu曲线具有相同的变化规律，但粘聚力不同，计算得出Pu值也不同。实验三各组Pu明显大于实验一，说明土体c值的增大，将直接影响地基极限承载能力。

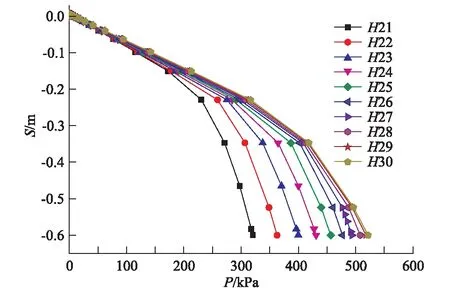
图10 H21～H30荷载沉降p-s曲线

见图11，实验一、三H～Pu曲线对比图，随着c的增加，地基极限承载力随之增加，但增大到一定程度，极限承载力增幅减小。曲线拐点大约在H=5 m处，即H/B=2.5处，在改变土体粘聚力的条件下，拐点依然与实验一、二结果一致。

图11 实验一、三 H-Pu曲线对比图

4.3 内摩擦角与持力层厚度的关系

地基土的φ同样也反映土体的抗剪强度的强弱，图12为H31～H40荷载沉降p-s曲线，由图可看出其与基础埋深、粘聚力对p-s曲线的影响机理一致。由图13可知，实验一、实验三、实验四3组H-Pu曲线具有相同的变化规律，但实验三各组Pu大于实验一，说明φ值的增大，能有效提高地基竖向承载能力。

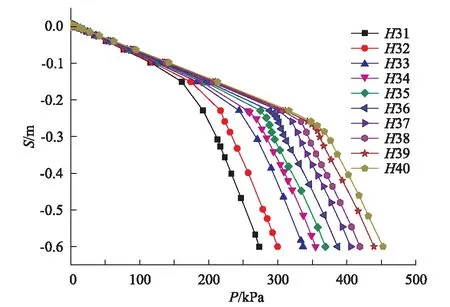
图12 H31～H40荷载沉降p-s曲线

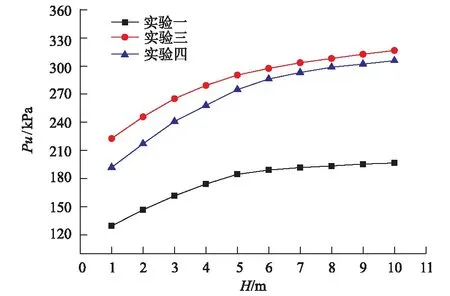
图13 实验一、三、四 H-Pu曲线对比图

如图13，实验一、三、四H-Pu曲线对比图，随着内摩擦角的增加，极限承载力随之增加，但增大到一定程度，极限承载力增幅减小。曲线拐点大约在H=5 m处，即H/B=2.5处，在改变土体内摩擦角的条件下，拐点规律依然未变。因此，在实际的浅基础工程设计中，尽量使得持力层厚度大于2.5B时，能减小持力层厚度变化对地基承载力的影响，达到发挥土体最佳承载能力。

取拐点H=5 m处的Pu值，3组数据见表5，比较得出：

表5 实验Pu数据

由实验三与实验一对比得：提高c值，将c增至2c，Pu值提高57.383%。

由实验四与实验一 对比得：提高φ值，将φ增至2φ，Pu值提高48.95%。

由实验三与实验四对比得：同比例提高c、φ值，提高c值，更好的提高地基承载能力，Pu值提高5.663%。

5 结论

本文从影响地基承载力的主要因素粘聚力c、内摩擦角φ、荷载q、基础埋深d、基础宽度b五个方面，基于Mohr-Coulomb模型。

通过对多组模型试验数据进行对比分析研究，得出以下结论：

(1) 当基础埋深D不同，而持力层厚度H相同时，增加持力层厚度H，Pu值逐渐增大，但两组实验得到的Pu值十分接近。说明基础埋深D的增加，对地基土竖向应力分布规律影响较小。

(2) 当基础埋深D与持力层厚度H不变时，提高粘聚力、内摩擦角能有效提高地基竖向承载能力。

(3) 基础底面放置在持力层上时，持力层厚度H较小，持力层厚度变化对地基竖向承载力影响大。随着持力层厚度H的增大，持力层厚度变化影响越小，临界点为H/D=2.5或H/B=2.5时，改变土体c、φ值，该规律依然存在，说明该规律适用于大部分土体中，因此在实际工程设计中，应当选择持力层厚度H大于2.5D或2.5B的地基基础，以达到发挥地基竖向承载力的最佳效果。

浅基础地基承载力影响因素众多，本文利用ABAQUS软件分析持力层厚度H变化在浅基础地基承载力中的影响规律，为今后浅基础设计提供一定的参考作用，为浅基础设计科学选址提供参考意见。