一类动力学网络上依赖时滞的相继滞后同步分析
2021-07-05李科赞
赵 杰, 李科赞
(桂林电子科技大学 数学与计算科学学院, 广西 桂林 541004)
同步是自然界普遍存在的一种现象,近年来学者们对其开展的相关研究深入到各个领域[1-3],如生物、力学、信息等,且有着重要的应用。滞后同步作为同步的一种重要模式,在网络领域已被广泛研究[4-6]。滞后同步定义在2个耦合网络中,xi(t)和yi(t)是2个网络中第i个节点的状态变量,当t→+∞时,有xi(t-τ)-yi(t)→0,τ>0,表示同步时滞,则称该耦合网络实现了滞后同步。为了实现滞后同步,文献[7-9]采用了牵制控制和自适应控制,网络模型都是基于完全同步提出的。
相继滞后同步是滞后同步的一种推广同步模式,近年得到广泛的研究。与滞后同步不同的是,相继滞后同步是在一个独立网络中定义的。xi(t)是网络中第i个节点的状态变量,网络的大小为n(或者网络的节点数为n),当t→+∞时,有xi(t-τ)-xi+1(t)→0,则称该网络实现了相继滞后同步。当n=2时,相继滞后同步就变成了滞后同步,而当同步时滞τ=0时,相继滞后同步就是完全同步。相继滞后同步现象在现实世界里普遍存在,如飞机编队的飞行等。
Li等[10]首次提出了相继滞后同步模式,并研究了受控的网络模型,得到了相继滞后同步的一些充分条件。文献[11-12]采用间歇采样控制和脉冲控制来实现网络的同步。这些研究都是基于受控下集中式的网络模型。相比集中式网络,分布式网络模型有更高的效率。因此,Li等[13]提出了新的分布式网络模型,为了更快更容易地达到同步,分别使用了2种反馈控制和自适应控制策略。Lu等[14]对新模型进行分析,得到了不加控制器下网络同步不依赖时滞的充分条件。
鉴于此,为得到依赖时滞的网络同步条件,对网络模型进行分析,通过构造李雅普诺夫函数,利用稳定性理论和矩阵理论得到了依赖时滞的网络同步的充分条件。选取3D神经网络作为网络的局部动力学,验证了理论结果的正确性。
1 预备知识
研究如下动力学网络模型[11]:


定义1[14]对任意初始条件xi(t)=φi(t)∈C[-(n-1)τ,0][10],若系统(1)的解满足:

则称相继滞后同步是全局渐近稳定的。
引理1[10]若g(t):R→R+在t≥0时为一致连续函数,且积分

定义2[14]QUAD(Δ,P,ω)函数类:设Δ=diag{δ1,δ2,…,δm}是对角阵,P=diag{p1,p2,…,pm}是正定对角矩阵,函数f(x,t):Rm×[0,+∞)→Rm,若存在ω>0,且对所有x,y∈Rm有:
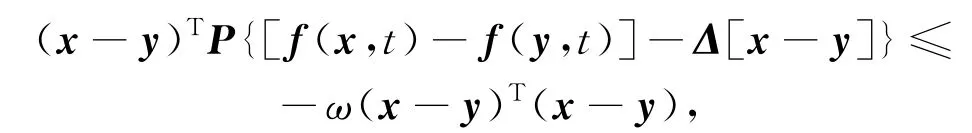
则f(x,t)∈QUAD(Δ,P,ω)。
引理2[15]对于合适维数的矩阵A1,A2,A3,A4和常数ϕ,矩阵的克罗内克积满足如下定律:
(i)(ϕA1)⊗A2=A1⊗(ϕA2);
(ii)(A1+A2)⊗A3=A1⊗A3+A2⊗A3;

2 依赖时滞的相继滞后同步分析
通过构造不同的李雅普诺夫泛函,再利用Barbalat引理分析网络相继滞后同步的稳定性,得到依赖时滞的2个同步充分条件。
定理1若矩阵B=(bik)(n-1)×(n-1),当i≠k时,满足bik≥0。f(x)∈QUAD(Δ,Im,ω),Δ=diag{δ1,δ2,…δn-1},ω>0。如果存在对角矩阵Λ=diag{α1,α2,…,αn-1},Θ=diag{ρ1,ρ2,…,ρn-1},Ξ=diag{ξ1,ξ2,…,ξn-1},h>0,使得:

且

证明 定义误差向量[11]ei(t)=xi(t-τ)-xi+1(t),i=1,2,…,n-1。于是误差系统为

构造李雅普诺夫泛函:
V(t)=V1(t)+V2(t)+V3(t),
其中:


V1(t)、V2(t)、V3(t)沿误差系统(4)的解的导数为:


从而,有:




定义分块对角矩阵:

其中:
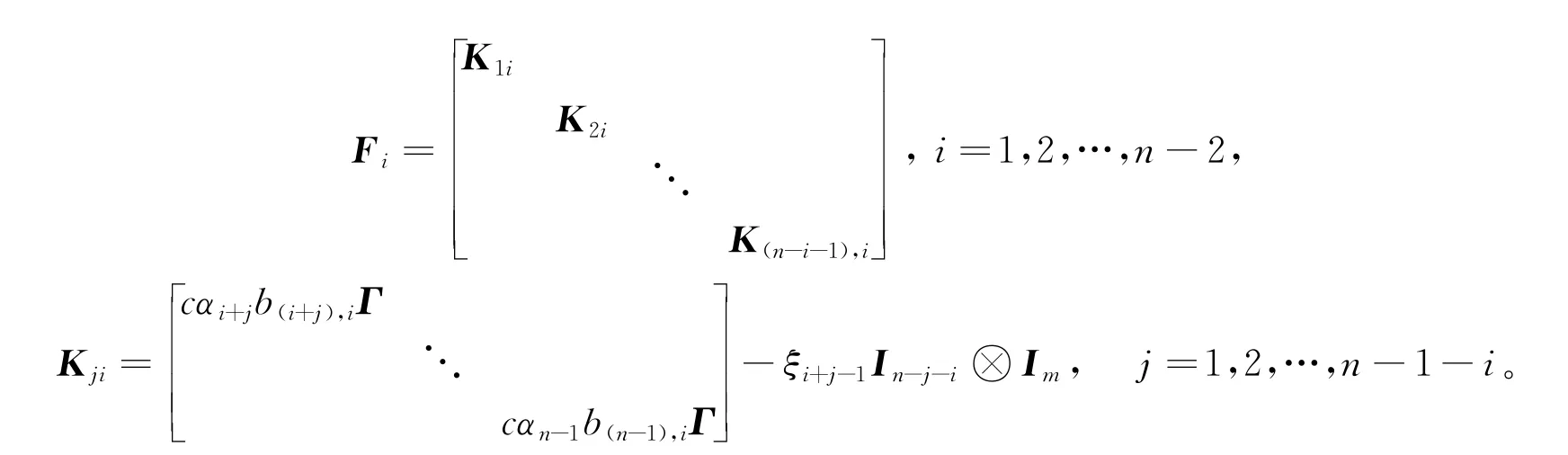
由定理1的条件(3)有:
F<0,
从而得到:

对式(5)从0到t积分有:

这意味着ei(t)→0,i=1,2,…,n-1。因此网络(1)的相继滞后同步是全局渐近稳定的。


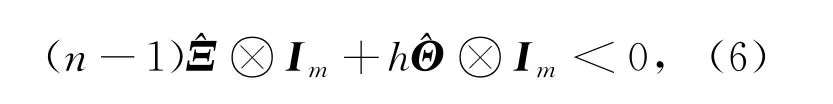
且

其中:

那么系统(1)的相继滞后同步是全局渐近稳定的。
证明
建立如下李雅普诺夫泛函:
H(t)=H1(t)+H2(t)+H3(t),
其中:

H1(t)、H2(t)、H3(t)沿 误 差 系 统(4)的 解 的 导数为:
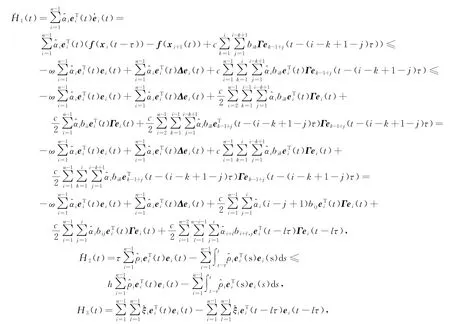
从而有:

定义分块对角矩阵:

其中:

根据定理2的条件(7),可得:
S<0,
进一步得:

对式(8)两边从0到t积分有:


定理2比定理1更为简洁,但定理1比定理2的条件弱,即当定理2的条件满足时,定理1的条件一定满足。因此,定理1的结果应用性会更强,定理2则更为简单。
3 数值模拟
为了验证理论的正确性,选择具体实例验证理论结果。不失一般性,选取如下的3D神经网络[15]作为网络节点的局部动力学:

其中:xi=(xi1,xi2,xi3)T∈R3;D=I3;

不失一般性,选取网络节点数n=10,网络耦合矩阵为


选 取Γ=I3,τ=0.2,c=10,Λ=0.1I9,Ξ=0.01I9,Θ=0.01I9,h=3。此时定理1的条件都满足,则在定理1的条件下,系统(1)在任意初值条件下都可以实现相继滞后同步。图1为系统的同步误差ei1、ei2、ei3的轨线。图2为在定理1的条件下系统(1)的状态变量xi1、xi2、xi3的轨线。从图1、2可看出,在同步时滞τ=0.2时,系统(1)实现了相继滞后同步。

图1 神经网络(1)的相继滞后同步误差(n=10,τ=0.2)
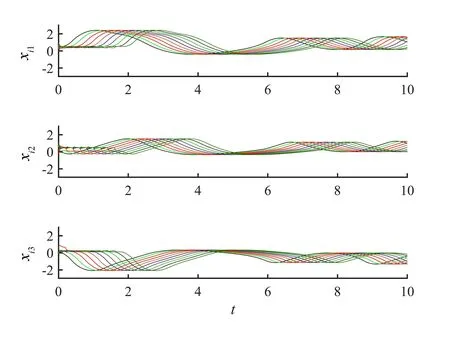
图2 神经网络(1)的状态变量(n=10,τ=0.2)
4 结束语
研究了一类新模型的相继滞后同步问题,得到了依赖时滞的同步条件。在现实中,系统往往存在时滞现象,因此依赖时滞的条件在实际中是有必要的。本研究是无控制条件的同步问题,今后将对网络加入控制器和加入的控制器的种类方法进行研究。
