求解非线性矩阵方程X+AiTX-niAi=Q的无求逆迭代算法
2021-07-05彭振赟
李 涛, 彭振赟, 王 杰
(桂林电子科技大学 数学与计算科学学院, 广西 桂林 541004)
讨论如下非线性矩阵方程的最大正定解问题:

其中Q∈Rp×p为对称正定矩阵,Ai∈Rp×p。

文中所用记号:Rp×p为所有p×p实矩阵的集合,N+表示正整数集合。对于矩阵A=(aij)∈Rp×p,用‖A‖F表示A的Frobenius范数,用A>0(A≥0)表示正定(半正定)矩阵A,若A-B>0(A-B≥0),则记作A>B(A≥B)。
1 无求逆迭代算法及其收敛性分析
非线性矩阵方程

对任意的非奇异矩阵X,设Y=X-1,代入方程(1),则有
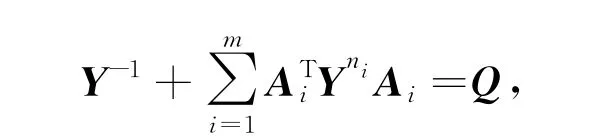
等号左右两边同时乘以Y,则转换为

算法1无求逆迭代算法求解方程(1)
1) 取定误差精度ε>0,输入Ai∈Rp×p,Q∈Rp×p为对称正定矩阵,Y0=Q-1,令k=0。
2) 计算
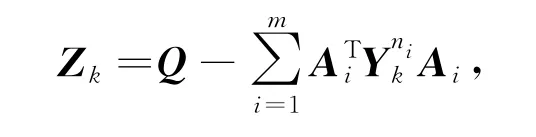
Yk+1=2Yk-YkZkYk。

引理1[19]当ni∈N+,Ai为非奇异矩阵时,若方程(1)有一个正定解X*,则

引理2[20]若B和C是相同阶的对称矩阵,且C>0,则
2B-BCB≤C-1。
引理3若方程(1)存在对称正定解X*,则



所以

又因为X*≤Q,则

因此,

定理1若方程(2)存在最小正定解Y*,{Yk}是由算法1生成的矩阵序列,初始值Y0=Q-1,则Y*是适定的,且0 证明设Y+是方程(2)的任意一个正定解,用数学归纳法证明对任意的自然数k,有0 当k=0时,Y0=Q-1, 由引理2和引理3可知, 所以k=0时,不等式成立。 假设k=t≥1时,0 由式(3)、(4)可知,0 通过数值实验来说明无求逆迭代算法对于求解方程(1)的可行性。所有数据均通过MATLAB R2016a,Windows 7 64 bit Intel®Core(TM)i5-6500处理器,3.20 GHz的PC获得。 为更加直观,考虑方程(1)的如下形式: 其中系数矩阵A1、A2为随机矩阵,Q为对称正定矩阵。算法终止条件为 其中ε=10-10为预设精度。 例1给定如下矩阵: 由算法1得到 这里‖Y9-Y8‖=8.740 9×10-11。所以Y9是方程(2)的最小正定解,即X9是方程(1)的最大正定解。 例2给定Q为单位矩阵I,A1,A2如下: 由算法1得到这里‖Y10-Y9‖=5.807 3×10-11。这表明,当Q为单位矩阵I时,用算法1解该方程依然有效,Y10是方程(2)的最小正定解,即X10是方程(1)的最大正定解。 针对非线性矩阵方程 的迭代法求最大正定解的问题,提出了一种无求逆迭代算法。该算法的优点在于,利用等价转换,构建了易于求解的迭代格式,避免了在迭代过程中反复求逆造成的数值不稳定。数值实验结果证明了可行性和收敛性,数值稳定,且迭代精度较高。
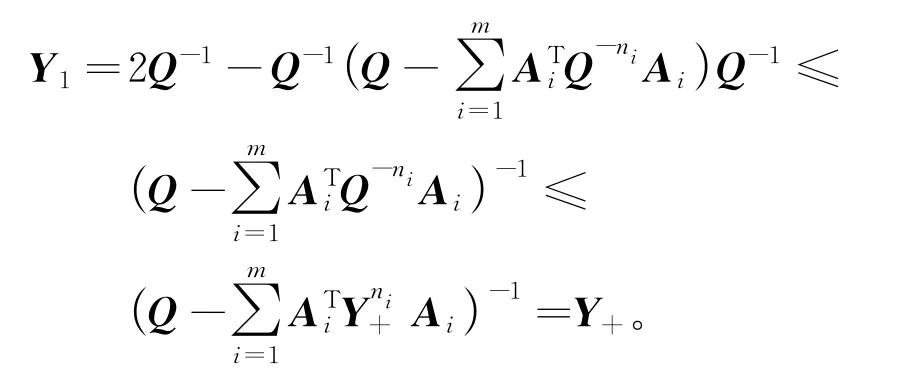

2 数值实验

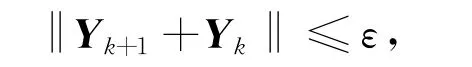





3 结束语

