LEA密码算法的积分区分器自动化搜索新方法

邱雪影, 韦永壮,2, 李灵琛,2

(1.桂林电子科技大学 计算机与信息安全学院,广西 桂林 541004;2.密码科学技术国家重点实验室, 北京 100878)

轻量级分组密码在许多资源受限的情境下(比如存储空间、功耗、计算能力等受限)具有特别重要的应用价值。轻量级分组密码算法的实用性设计和自动化分析一直是业界讨论的热点问题。目前国际上公开的一系列轻量级分组密码算法包括Midori[1]、Piccolo[2]、MIBS[3]、Height[4]、LED[5]、LBLOCK[6]等。这些算法不但能在资源受限的终端设备快速稳定运行,而且具有占用芯片面积小,消耗能耗低,存储资源少及安全性刻画清晰等优点,备受业界青睐。

轻量级分组密码的分析技术与设计技术相伴而生,相互促进和发展。积分密码分析是度量轻量级分组密码安全性的重要手段,最早由Kundsen等在文献[7-9]中讨论。随后,Z’aba等[10]在2008年快速加密软件国际会议上提出了比特级模式的积分攻击,使得积分分析方法趋于完善。2016年Xiang等[11-14]将混合整数线性规划(MILP)的思想结合可分性概念,并实际运用于积分分析。该工作还针对6个轻量级密码算法进行模型构建,由此产生一系列的线性不等式。随后,通过利用Gurobi求解器搜索,捕获新的积分区分器。此外,在2013年信息安全应用国际会议上,轻量级分组密码算法LEA[15]被提出,其采用4分支的Feistel结构,且内嵌ARX运算,具有实现速度快,适合各种软硬件实现等优点,备受广泛关注。2016年Sun等[16-17]使用模加运算的迭代表示构造比特级可分性的模加运算模型,并给出了LEA算法的一个8轮区分器。2017年Sun等[18]提出利用自动化工具来搜索ARX密码的可分性以及基于字级的一些密码算法的可分性的进展。2018年,Sun等[19]提出了一种基于非比特置换算法的建模方法,将一个复杂的线性层分解为复制和异或操作,然后逐个对这些基本操作建模。2019年Zhang等[20]提出了一种扩散层的可分性新方法。2020年张景芝[21]对轻量级密码算法的设计进行分析和总结。2020年Hu等[22]建立了一个新的模型,该模型只包含与一条有效路径对应的子矩阵。同年,Hao等[23]提出了一种使用自动化工具进行三子集可分特性建模的方法,对此进行立方攻击。2020年,李航等[24]利用中间相错技术再次分析了LEA算法,得到了9轮积分器。LEA密码算法是否存在更高轮数的区分器及破译方法是目前亟待解决的问题。

基于LEA密码算法的整体结构,结合BEIERLe等[25]在2020年美密会上给出的模加运算的可分性建模方法,提出一种结合MILP新模型捕获到积分区分器的自动化搜索方法。在Gurobi求解器环境下,证实了LEA密码算法存在10轮和11轮积分区分器。与已有结果相比,该方法捕获了更高轮数的新区分器。

1 LEA密码算法的介绍

LEA算法是Hong等[15]在2013年信息安全应用国际会议上提出的一个轻量级分组密码算法。其分组长度128 bit,且可选密钥分为128、192及256 bit,分别表示为LEA-128、LEA-192和LEA-256。以上表示方法所对应的轮数分别为24、28及32轮。

LEA使用以下符号:

1)明文P: 4个32 bit的字(128 bit),可表示为P=(P[0],P[1],P[2],P[3])。

2)密文C:4个32 bit的字(128 bit),可表示为C=(C[0],C[1],C[2],C[3])。

3)中间变量Xi:第i轮加密函数的输入,4个32 bit的字(128 bit),可表示为Xi=(Xi[0],Xi[1],Xi[2],Xi[3])。

4)Lx:字符串x的比特长。

5)轮数r:当LK=128;r=24;LK=192;r=28;LK=256;r=32。

6)所有轮密钥的连接RK:定义为RK=(RK[0],RK[1],…,RK[r-1]),其中RKi是第i轮的192 bit的轮密钥,其中RKi由6个32 bit的字组成,即RKi=(RK[0],RK[1],…,RK[5])。

7)x⊕y:相同长度的比特串x和y的异或。

8)x□+y:32 bit字符串x和y对232取模。

9)ROLi(x):在32 bit的值x上左移ibit。

10)RORi(x):在32 bit的值x上右移ibit。

LEA算法的加密流程:将128 bit中间值X0设置为明文P。加密算法中,轮函数包括模加运算、异或运算和循环移位,调用密钥编排算法生成r轮子密钥。第i轮 的128 bit输出Xi+1=(Xi+1[0],Xi+1[1],Xi+1[2],Xi+1[3]),i≤0≤r-1,可被计算为:

Xi+1[0]←ROL9((Xi[0]⊕RKi[0])(Xi[1]⊕RKi[1])),

Xi+1[1]←ROR5((Xi[1]⊕RKi[2])(Xi[2]⊕RKi[3])),

Xi+1[2]←ROR3((Xi[2]⊕RKi[4])(Xi[3]⊕RKi[5])),

Xi+1[3]←Xi[0]。

密文C经过循环迭代后,由最终得到的Xr生成,即C[0]←Xr[0],C[1]←Xr[1],C[2]←Xr[2],C[3]←Xr[3]。具体过程如图1所示。

图1 LEA加密算法

2 比特可分特性的MILP模型

2.1 可分性及其传播

可分性定义[13]定义X为一个多重集,其中的每个元素都属于()m。K(l),l=0,1,…,q-1表示m维向量集合,第i个元素的取值范围为[0,1,…,n]。若这个集合有可分特性,则满足如下条件:位比特函数

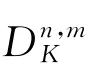
对于所有的i∈[1,2,…,r],从ki-1传播到ki,且(k0,k1,…,kr)∈K0×K1×…×Kr,最后,用向量集合Kr判定是否存在有效的积分区分器。因此,称(k0,k1,…,kr)为r轮可分轨迹。

2.2 MILP的简介

MILP(mixed integer linear programming)在商业和经济中经常被用于解决优化问题。MOUHA等[11]提出了一种基于MILP的自动搜索方法。然而,该方法的缺点是所提出的约束不能描述线性扩散层的差分传播轨迹。近年,也有许多密码分析人员将MILP方法应用到常用的差分分析、线性分析、积分分析等的密码分析方法上,详细地描述线性扩散层的差分传播轨迹。MILP模型用N表示,涉及的变量用N.var表示,约束用N.con表示,目标函数用N.obj表示。一个简单示例可以描述MILP求解过程如下:限制条件为p=x+y+2z,求p的最大值。

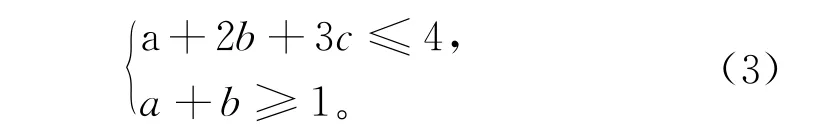
在本例中,目标函数的定义域由2个不等式和一个约束条件决定,得到目标函数在该域中的可行解。其最大值为3,对应(a,b,c)=(1,0,1)。

MILP应用实例说明:一组线性不等式T(例如在Sage软件中使用inequality_generator()函数),所有满足条件的解都包含在这一条可分路径上。通常,MILP问题的目标是快速地找到给定问题的可行(或最优)解。在基于比特可分性的背景下,构造了一个MILP模型来描述积分特性的传播轨迹。这个过程代表了一个自动化搜索积分区分器的过程,则一个完整的MILP问题可以用N(T,obj)来刻画。在模型构建方法中,所构建的MILP模型将通过开源数学优化软件Gurobi进行求解。

2.3 比特级可分性的MILP模型描述

以下是3种基本操作中的可分性变化关系[12]:

初始可分特性和停止规则:首先考虑多重集X,且可分性可表示为D,然后定义ei为长度为n的向量(也可称作为单位向量),其第i个坐标是唯一的非零坐标。在此说明了如何通过检查Kr+1是否包含所有ei(i=1,2,…,n),更准确地说,若能在集合Kr+1中找到所有的单位向量ei(每个ei∈Kr+1)。则意味着不存在任何r轮可分轨迹。同样,若存在ei,使ei,则表示可以找到r轮积分区分器。设Y表示对输入集合X执行的r轮加密的输出。假如Y是没有任何可利用的积分性质,则Y的所有向量的异或和对于每个比特都是未知的,这也意味着⊕y∈Yπei(y)这一可分性质对于任何的单位向量ei∈来说都是未知的情况,其中i=1,2,…,n。反之,若存在至少一个不属于K的单位向量ei,则在第i个位置的值总是等于零,即可以找到一个r轮的积分区分器。

搜索终止后,即可确定最终的积分区分器的平衡位置与未知位置。

3 LEA算法的建模搜索

在可分性传播过程中,可分性不会受其轮密钥加的影响而改变,故只考虑模加运算和置换操作对可分性的影响。在MILP模型中将ARX运算和分支结构分解为异或和复制操作,即可基于比特可分特性的单个轮函数的加密操作,使用MILP模型得到多轮可分性的传播。

对于具有ARX结构的分组密码来说,模加运算是一种重要的非线性运算部件。对该部件的具体建模如下:

假设x=(x0,x1,…,xn-1),y=(y0,y1,…,yn-1)和z=(z0,z1,…,zn-1)是nbit向量,且z=xy。模2n可表示为z=(x+y)mod2n(十进制形式),然后zi的布尔函数(二进制迭代建模)可用下列式子表示:

定义向量x,y,z属于Fn2,其中xn-1,yn-1,zn-1,cn-1为最低位,同时定义函数(ci,zi+1)=f(xi+1,yi+1,ci+1),可得到如表1所示的真值表。

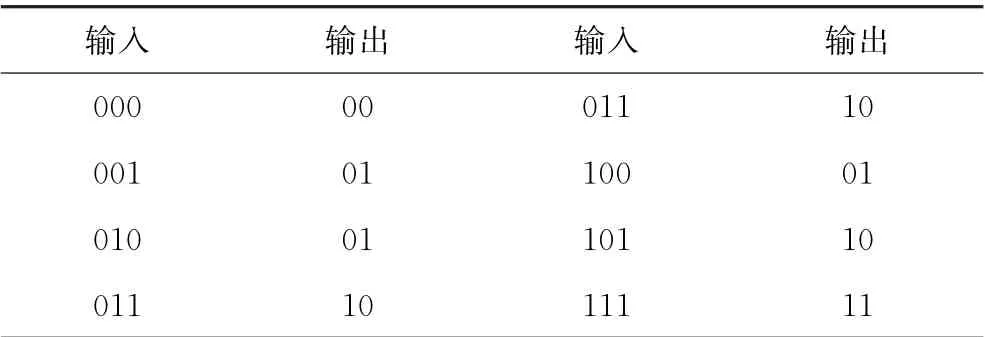
表1 函数(ci,zi+1)=f(xi+1,yi+1,ci+1)对应的真值表

用式(7)迭代表达式,可以逐步地对模加运算建模。以4 bit(n=4 bit)模加运算为例,迭代表达式zi(i=0,1,2,3)可表示为

Beierle等[25]在2020年美密会上给出了模加运算的一种可分性建模方法。其优点是减少不等式的个数,降低求解复杂度。利用表1的真值表,得到函数(ci,zi+1)=f(xi+1,yi+1,ci+1)对应的可分轨迹,如表2所示。

表2 函数(ci,zi+1)=f(xi+1,yi+1,ci+1)对应的可分性传播轨迹

由表2给出的可分性传播表具有以下不等式的特征:

其中:x,y,c∈Z2对应于输入可分性;c',y∈Z2对应于输出可分性的值。本实验中,这2个不等式应用于每个比特的位置,精确地生成了n到7的加法模2n的可分性传播表。

将可分轨迹作为Sage中Inequality_generator()函数的输入,得到以下表达式:

(-1,-1,-1,1,2)x+0≥0,

(0,0,1,0,0)x+0≥0,

(0,0,0,1,0)x+0≥0,

(0,0,-1,1,1)x+0≥0,

(1,0,0,0,0)x+0≥0,

(1,1,1,-1,-1)x+0≥0,

(0,1,0,0,0)x+0≥0,

(-1,0,0,1,1)x+0≥0,

(0,-1,0,1,1)x+1≥0,

(0,-1,0,0,0)x+1≥0,

(0,0,1,-1,-1)x+1≥0,

(0,0,0,0,-1)x+1≥0,

(0,0,-1,0,0)x+1≥0,

(1,0,0,-1,-1)x+1≥0,

(1,1,1,-2,-2)x+1≥0,

(0,1,0,-1,-1)x+1≥0,

(-1,0,0,0,0)x+1≥0。

用贪婪算法对表达式进行缩减,可得到模加运算第i个分量对应的可分性传播模型:

其中,0≤i≤n-1。

对LEA进行r轮搜索后,对基于比特可分性进行建模的MILP实例已执行了r次,因为需要检查所有单位矢量是否都包含在中,作为停止规则。最后,若求解器可以为特定的MILP实例找到可行的解决方案,则将确定LEA算法存在r轮区分器。

4 应用于LEA算法的搜索结果

基于前面讨论的方法,对LEA算法进行完整的MILP建模,利用Gurobi求解器进行区分器的搜索。采用的搜索工具为Python 2.7,建模工具为Sage-Math 8.3,Gurobi 8.1.0。

4.1 LEA的10轮积分区分器

当选取明文输入的活跃比特a的位置第0 bit到第43 bit、第47 bit到第127 bit,固定比特c从第44、45、46 bit时,进行10轮加密后,将相应的结果进行求和,则发现第9, 10, 11, 12, 13, 14, 15, 16, 17,105, 106, 107, 108, 109, 110, 111, 112, 113, 114,115, 116, 117, 118 bit (即平衡比特b的位置)的异或值为0,其余位置(即?的位置)的比特的值为未知。这本质上提供了一种10轮积分区分器:

输入:a32,a12c3a17,a32,a32。

输出:?14b9?9,?32,?26b6,?9b14?9。

4.2 LEA的11轮积分区分器

如果活跃127 bit,可得到LEA算法11轮积分区分器,即选择输入的第32 bit为固定比特,其余位为活跃比特位。经过11轮加密后得到有效的区分器如下:

输入:a32,c1a31,a32,a32。

输出:?32,?32,?32,?9b10?13。

当选取明文输入和进行遍历时,有126 bit为活跃位置的比特(即a的位置),1 bit的值不变(即固定比特c的位置)。以上明文数据进行11轮加密后,将相应的结果进行求和,则第105, 106, 107, 108,109, 110, 111, 112, 113, 114 bit (即平衡比特b的位置)的异或值为0,其余比特位置(即?的位置)的值为未知。

表3为LEA已知的区分器的对比情况。由表3可知,新提出的搜索算法捕获了更高的区分器轮数,进一步证实了该方法的有效性。

表3 LEA的区分器结果比较

5 结束语

基于LEA轻量级分组密码算法的轮函数结构的构造特点,构建了比特级可分性的MILP模型,并基于此提出一种捕获积分区分器长度的自动化搜索新方法。利用 Gurobi求解器,实验捕获了该算法的10轮及11轮积分区分器。这些LEA的新区分器比以往的区分器具有更高的轮数,这些都说明该自动化搜索方法是有效的。然而,如何优化建模,在提高攻击轮数的同时,大幅减少攻击所需的数据复杂度及时间复杂度是下一步需要研究的问题。