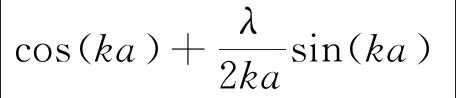一维周期性δ函数势场中束缚态能级的研究①
2021-07-05田路遥张澜旭裴魏魏张海丰
田路遥,张澜旭,裴魏魏,*,张海丰
(佳木斯大学a.理学院,b.机械工程学院,黑龙江 佳木斯 154007)
0 引 言
在初等量子力学中,求解一维薛定谔方程能够给出量子体系的严格的能级分布和波函数,其关键在于知道体系的势能函数分布,δ函数势场是典型的势能函数之一,因而被广泛的研究与应用[1-4]。例如,黄明举对有限长周期δ势阱和势垒中的原子链模型的薛定谔方程进行了递推法求解,给出了计算机计算时确定能级的递推公式[5];井孝功等在给定的极限条件下,方势垒(阱)的本征解与δ势垒(阱)的本征解一致[6];唐义甲等通过对添加δ势垒的一维半无限深势阱的薛定谔方程进行求解,得到了粒子运动的波函数和能级的相关公式[7];唐世清等求解了一维δ势阱的束缚态问题[8]。旨在通过求解一维周期性δ函数势所满足的薛定谔方程,给出系数方程组的系数矩阵,进而给出束缚态能级。
1 一维势场中的波函数
设质量为m的粒子约束在一维势V(x)中,在某些区域V(x)是常数V(x)=V。在此区域内,E>V,E 易知,体系的定态波函数满足的薛定谔方程为 (1) E>V时,令ћ2k2/2m=E-V,于是有 (2) 该方程的解可以写成 φ(x)=Aeikx+A'e-ikx (3) 的形式,这里的A是A'是任意复常数。 E (4) 上式的一般解是 φ(x)=Beρx+B′e-ρx (5) 这里B和B'是任意复常数。 E=V时,可得 (6) 上式的解为 φ(x)=Cx+C′ (7) 这里C是C'是复常数。 设质量为m,能量E>0的粒子被束缚在一维势-V0δ(x-a)中,下边讨论取极限ε→0时的定态薛定谔方程,进而给出束缚态波函数的跃变条件。 易知,体系的薛定谔方程可以写为 (8) 对上式在a-ε和a+ε之间进行积分 (9) 根据波函数φ(x)的自然条件,在区间[a-ε,a+ε]上,当ε→0时,可得 (10) 在x=a处,φ(x)的导数发生跃变 2mV0φ(x)/ћ2 (11) 由φ(x)在x=a连续性条件,可以得到 (12) 由式(11)和(12)可得 (13) 所以可以得到系数满足的方程组为 (14) 因而,有 (15) 设质量为m的粒子被束缚在周期性的δ函数势场中,周期势表示为 (16) 对于每一个na φn(x)=Bneik(x-na)+Cne-ik(x-na) (17) 则在n+1区域内的系数关系矩阵为 (18) 根据T的非奇异性,可以得到矩阵T的本征向量为 (19) 式中:β1和β2是复数。 在n和n+1两个区域的x=(n+1)a处按照边界条件可得 (20) 其中系数满足如下矩阵 (21) (22) 由于 (23) 可见T不是奇异矩阵detT≠0。 根据T的非奇异性,令C2的本征值为α1和α2,则有 (24) 则由式(18)可以得到 (25) 当|α1|≤1时 (26) 当|α2|≤1时 (27) 对于n→-∞的情况,可得 (28) 当|α1|=|α2|=1时,T的本征值方程为 det(T-eiφI)=0 (29) 式中:φ是实常数,I为单位矩阵,于是 (30) 整理上式可得 (31) 上式的实部为 (32) 由cos(2φ)=2cos2φ-1及可以得到 (33) (34) 可以通过对函数 (35) 描点法给出相应的能级。当k→∞时,函数f(k)近似为cos(ka)。可见相应的能量E并不对应一个可能的态,而是被|f(k)|≥1区域隔开的可能能量分布;当E→∞,能级分布的禁带将变得很窄,从而可以得到能级的连续谱。2 一维δ函数势场中束缚态本征函数的跃变条件
3 周期性的δ函数势场中粒子的束缚态能级
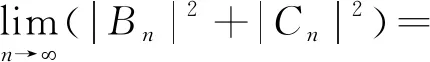
4 结 语