基于脉冲控制的线性多智能体系统的二部一致性①
2021-07-05周金连刘东南
周金连, 刘 琛, 刘东南
(湖南工业大学理学院, 湖南 株洲 412007)
0 引 言
近些年来,多智能体系统的协调控制广泛应用于各个方面,如多刚体系统的姿态同步控制[1],无人机编队[2]和传感器网络[3]等工业和军事领域中,由此吸引了众多研究者的兴趣.一致性的目标是系统通过一下合适的分布式控制使得个体所有的状态达到如期的一个状态值.
在多智能体一致的研究中大部分只考虑个体间只有合作关系.然而,在现实的系统中,个体间不仅有合作关系,还有竞争关系,它们之间的关系分别用正负权值表示.因此,具有正负关系的多智能体系统成了近年来多智能体系统研究的一个新趋势[4-7].如在文[4]研究了符号网络下多智能体系统的二部一致性问题.文[5]研究了一类具有合作-竞争关系的一般线性多智能体系统的输出调节问题.文[6]考虑了具有敌对关系的时变时滞多智能体协调二部一致.文[7]研究了信息交流具有间歇交互的一阶多智能体系统二部一致.以上所述的成果大部分是一阶和二阶系统的,而高阶动态系统控制协议的设计更具有挑战性,所以研究了高阶线性动态方程的多智能体系统.
脉冲控制是多智能体系统重要的一个控制方法,在复杂网络的研究中应用极其广泛,它具有控制量小、收敛性高、控制成本低等优点.为此,脉冲控制方式显得更重要[8-10].文[8]研究了混杂脉冲控制下二阶非线性的保性能双向编队控制一致性问题.文[9、10]设计了脉冲控制协议,使得二阶多智能体系统实现了二部一致性.目前,关于合作-竞争网络下多智能体系统采用脉冲控制方法的研究成果还较少,本研究采用脉冲控制方法.
1 预备知识与问题描述
1.1 预备知识

定义1[4]对于符号网络G=(V,E,A)的权重矩阵A=[aij]∈RN×N,若存在一个节点集合V的二元划分为V1和V2,且同时满足:V1∩V2=Ø,V1∪V2=V;∀(i,j)∈Vq,有aij≥0;∀i∈Vq,∀j∈Vp,有aij≤0,其中q,p∈{1,2},则称G是结构平衡的.
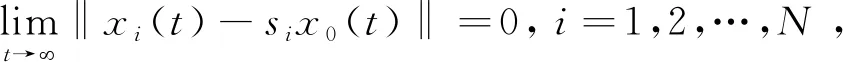
假设1假设拓扑图G是结构平衡的.
引理1[4]连通符号拓扑图G(A)是结构上平衡的,当且仅当下列等价条件之一成立:
(1)G(A)所有的周期都是正的;
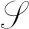
(3) 0是L的一个特征值.
1.2 问题描述
考虑由N个跟随者和1个领导者构成的多智能体系统,第i个智能体和领导者的动态方程为:
(1)
(2)
其中,xi=[x1T,x2T,…,xNT]T,Α∈Rn×n是常数矩阵,xi(t)∈Rn,ui(t)∈Rp分别代表第i个智能体的状态和控制输入,x0(t)∈Rn代表领导者的状态.
系统在脉冲控制下的动态方程具体描述如下:
(3)
其中△tk=tk-tk-1≤μ<∞为脉冲期间,常数c>0表示耦合强度.
根据脉冲控制的特点,设计了如下的一致性协议:
(sgn(aij)xj-xi)-hi(xi-six0))
(4)
其中符号函数sgn(·)满足sgn(aij)=1,aij>0,sgn(aij)=0,aij=0,sgn(aij)=-1,aij<0;tk表示脉冲时刻,且0=t0 当t≠tk时,定义误差系统为ei=xi-six0,对以上误差系统进行求导: (5) 当t=tk时,有 △ei(tk)=ei(tk+)-ei(tk)=Δxi(tk)=cui(tk) (6) 把(4)式代入(6)式得 (xi-sgn(aij)xj)-hiei) (7) 由于si2=1,|aij|=siaijsj,sisgn(aij)sj=1,因此等式(7)可写成 siaijsjsgn(aij)ej-siaijsjsgn(aij)sjx0)-hiei)= (8) (9) 综上所述,误差系统为: (10) 证明:当t≠tk时,构造下列李雅普诺夫函数 (11) 函数(11)对时间t求导可得: (12) 解得上式V(t) 当t=tk+时,有 (13) 图1 多智能体系统拓扑图 当t=tk-1+时,有 (14) 所以当t∈(tk-1,tk]时, V(tk) (15) (15)代入(14)得 依此类推,当t=t0+, (16) 所以t∈(t0,t1],V(t1) 通过迭代计算可得: 图2 智能体的运动轨迹图 图3 智能体的运动轨迹图 讨论了合作-竞争网络下的多智能体系统的脉冲控制二部一致性问题.通过设计合理的控制输入协议,利用代数图论、规范变换、稳定性理论等相关理论知识,得到了线性多智能体系统实现二部一致性的充分条件.最后,通过仿真的例子验证了结论的有效性.


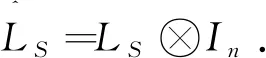
2 脉冲控制的二部一致性分析
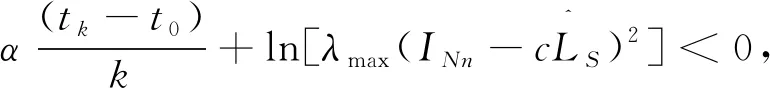
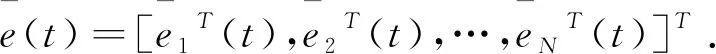
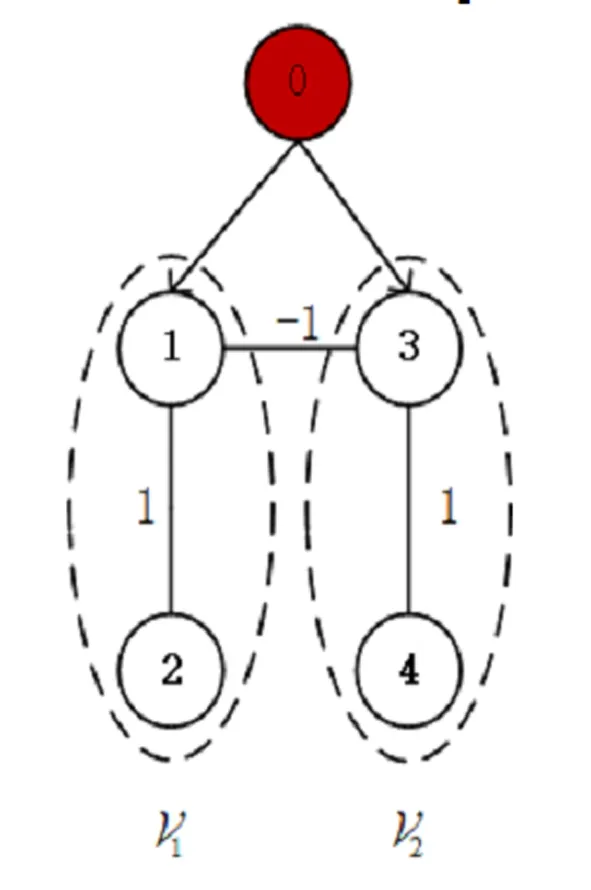
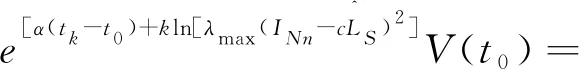
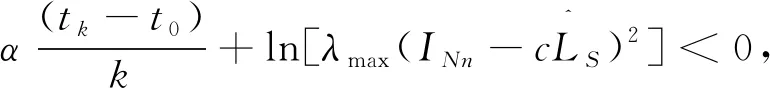
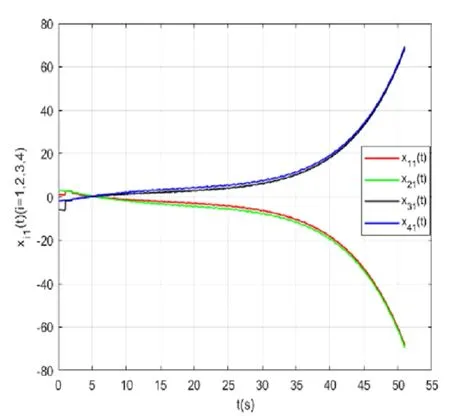

3 数值仿真
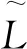
4 结 论
