双目摄像机标定及校正算法
2021-07-05侯一民洪梁杰
侯一民 洪梁杰
(东北电力大学自动化工程学院,吉林 吉林 132012)
0 引言
近年来,随着计算机性能的不断提高和图像处理技术的不断突破,计算机视觉技术在健康医疗、智能监控、机器人以及无人驾驶等诸多领域得到了广泛的应用。在计算机视觉研究领域,双目立体视觉是一项非常重要的研究内容,其利用双目摄像机模仿人眼,基于视差理论实现三维测距与定位。目前,双目立体视觉得到了世界各国研究机构的全力投入与支持,在理论以及实践应用方面取得了不错的成果。例如,微软公司与美国华盛顿大学联合研发了一套基于立体视觉技术的道路导航探测系统,该探测系统成功地应用于复杂火星环境下的火星探测车“探测者号”的视觉导航。美国麻省理工学院将双目立体视觉与雷达系统融合,并巧妙地将其应用于道路交通领域。浙江大学开发出一种番茄采摘机器人,其使用双目立体视觉技术有效地解决对遮挡番茄以及成簇番茄的识别和三维定位[1]。哈尔滨工业大学提出异构双目视觉系统,并将其成功应用到了足球机器人的导航系统中[2],这是一种结合了固定摄像机和可旋转摄像机的异构双目模型,实现了在无传感器工作的环境下保持基础导航的功能。对双目摄像机进行标定与校正是研究立体视觉的前提,其标定方法和立体校正方法对立体视觉系统的研究有非常重要的作用。
1 双目摄像机标定及立体校正
双目视觉的基本原理是借助2个视点观察同一景象来获取在不同视角下的感知图像,然后利用三角测量原理计算图像像素间的视差,进而重建其三维空间信息。该过程类似于人类视觉的立体感知过程。一个完整的双目立体视觉系统可以分为数字图像采集、相机标定、图像立体校正、立体匹配以及三维重建等。图1展示了理想状态下双目平行的立体视觉三维模型。
如图1所示,在理想状态下,光学参数完全相同的左、右2台摄像机都满足线性成像模型,并且处在同一高度,左右光轴相互平行。左摄像机的坐标系为Ol-xlylzl,其对应的物理坐标系为Ol-xlyl,其中xl、yl分别与左摄像机成像平面的竖直、水平方向垂直,Ol为光轴与左摄像机成像平面的交点;右摄像机的坐标系为Or-xryrzr,其对应的物理坐标系为Or-xryr,其中xr、yr分别与右摄像机成像平面的竖直、水平方向垂直,Or为光轴与右摄像机成像平面的交点。在空间中任取一点P(X,Y,Z),点P在左右摄像机上的成像点分别以Pl(xl,yl),Pr(xr,yr)表示,f代表有效焦距,B为左右摄像机光心Ol、Or之间的距离,也称作基线距离。在计算中假设左目相机的坐标系与世界坐标系重合,就能够通过计算求得目标在三维空间中的坐标信息,如公式(1)所示。


图1 双目立体视觉系统三维模型
在公式(1)中,xl、xr代表点P在左右摄像机成像平面上所形成的视差d,即空间中一点在双目图像中的位置差异。图2为双目立体视觉系统深度计算的示意图。

图2 平行双目视觉深度信息测量系统深度计算示意图
如图2所示,Ol、Or分别为光轴与左右摄像机成像平面的交点,Ol、Or为左右摄像机的光心,pl、pr为空间内任一点P在左右摄像机上的成像点,Z表示深度。根据相似三角形的基本原理,可以推导出深度公式,如公式(2)所示。

由公式(2)可以得出深度与视差之间呈反比例,即求得的深度值随着视差值的减小而增大;反之,得到的视差越大,求出的深度值则越小,如图3所示。

图3 深度与视差关系图
通常先用单摄像机的标定分别得到2个摄像机的内、外参数,进而得到物点与像点间的映射关系。摄像机标定参数见表1。表1中A为相机的内部参数矩阵;fx、fy为像平面中的有效焦距[3],u0、v0为图像的的中心点,即主点的像素坐标,γ为相机2个坐标轴之间的不垂直因子(理想情况下不垂直因子为0);k1、k2为径向畸变系数,p1、p2为切向畸变系数,R、T分别为摄像机位置变化的方向(旋转矩阵)与位置(平移矩阵)关系。
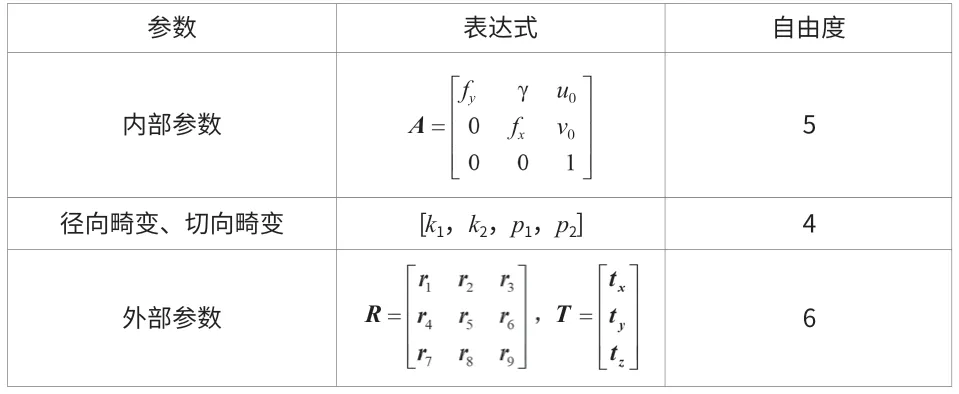
表1 摄像机标定参数
双目立体视觉系统中最重要的一步就是匹配问题,即在右摄像机成像平面中寻找匹配点pr与左摄像机成像平面上的某点pl相对应,为了避免在全局进行扫描搜索,可以根据极线几何理论,确保匹配点一定在待匹配点pl的对应极线上,这样就可以在极线上搜索并快速找到匹配点,从而实现高匹配精度和高准确率的效果。
事实上,由于相机内部构造以及相机的摆放位置和方式都会对实验造成一些误差,因此要保证2个摄像机的图像的行对准,使立体匹配更可靠、计算更可行,就还需要对图像对进行立体校正,从而确保2张图像的极线能够平行,且左右图像对应的像素在同一条直线上,提高匹配的可靠性和算法的效率。
目前关于立体校正的算法有Hartley和Bouguet算法,它们分别是针对未知参数和已知参数的校正方法。该文所选用的立体校正算法是Bouguet算法。
2 该文摄像机的标定及校正方法
2.1 摄像机标定结果与分析
该文采用黑白相间的棋盘作为标定板,黑白方格相交的点称之为角点,角点更有利于像素点的定位与测量。整个过程大致可以分为2个部分:1) 分别对左、右摄像机进行单目相机标定,得到左摄像机和右摄像机的标定参数。2) 进一步计算左右摄像机之间的旋转矩阵和平移向量,完成立体标定。图4为该文的棋盘格标定板,其大小为20 mm×20 mm,格数为6×11格。

图4 棋盘格标定板
2.1.1 图像采集
首先固定摄像机;其次,在不同角度和位置采集棋盘格标定板的图像。为了能够得到更加精确的标定信息以及保证棋盘格在图像中占有足够比例,该实验设定采集10幅以上的标定图像。
2.1.2 角点提取
在采集待标定图像后,需要对图像棋盘格的角点进行提取和检测。图5是一幅左目图像的角点提取结果,即棋盘方格中小正方形的4个顶点,图中黑色方框所涵盖的范围是角点所在的区域,叉号表示识别出来的角点,该结果共提取了66个角点,选取左上角的第一个角点作为世界坐标系的坐标原点,Z轴垂直于模板平面,并且指向模板外,根据右手规则确定X、Y轴,创建世界坐标系,棋盘格平面就是世界坐标系的平面。

图5 角点提取结果
2.1.3 算法标定
摄像机标定图像采集,完成角点提取步骤后,再进行张正友算法标定。该标定方法是介于传统标定算法与自标定算法之间的一种灵活度与准确性比较高的方法,其标定过程如下:首先,摄像机采用线性成像模型,在不考虑光学畸变的情况下通过单应性矩阵求出摄像机的标定参数;其次,引入畸变模型,求解出在线性模型下的相关参数;最后,将参数作为初始值对其进行非线性化优化,获取最终的模型标定参数。因为实验中标定图像大小是1280×720dpi,所以理想主点坐标应为图像的中心位置,即(640,360);而标定结果左右图像的主点坐标分别为(690,368)和(669,377),虽然与理想标定结果有一定的误差,但是都在合理的误差范围内。
双目相机标定参数中的旋转矩阵R表示双目相机的旋转关系,可以通过Rodrigues算法转换为矩阵形式。平移向量T代表右目相机相对于左目相机的距离(该文以左目相机为坐标轴原点),该文所用的双目相机的基线距离为43 mm,与标定结果42.9 mm近似相等,其他2个方向的距离很小,与实际情况相符。
2.2 立体校正实现
该文利用Open CV工具箱对图像进行图像剪裁、Bouguet校正以及消除畸变等操作。首先,利用径向和切向畸变系数矫正图像对;其次,输入标定参数,并用stereo Rectify函数与initUndistort-Rectify Map函数得到平移与旋转参数;最后,用remap函数得到校正后的图像对。立体校正前、后的图像对如图6和图7所示。
对比图6和图7可以看出,经过校正的图像实现了左右2幅图像的行对齐,每一行都能够沿着极线在水平方向上对齐。

图6 未经校正前的图像

图7 立体校正后的图像
3 结论
该文首先介绍了双目立体视觉的基本原理;其次阐述了关于相机标定和立体校正的相关内容;再次,详细介绍了相机标定实验,并针对相关图像数据进行分析;最后,通过OpenCV中提供的相关函数并结合标定参数对双目图像进行立体校正,实现了行对齐。该文完成了双目立体视觉研究的前期工作,即通过标定方法获取标定参数,利用标定参数完成图像对的立体校正,使图像对实现行对齐。在双目立体视觉研究的后期,还需要使用立体匹配算法,通过视差值的计算得到图像对的深度图,进而根据成像原理和双目测距原理实现三维重建。
该文在实际的标定过程中,遇到的实验条件可能是复杂多变的,为了获得更加准确的成像效果,需要不断调整摄像机的焦距,从而使摄像机的内外参数发生了变化。因此,接下来在相机标定方面的研究重点主要在于对图像的快速自标定方法进行研究,进而提高标定的实时性。
