轴支架双桨船附体阻力尺度效应数值分析
2021-07-05韦红刚詹明珠
韦红刚 詹明珠 冯 毅 孟 阳 于 海
(1.上海市船舶工程重点实验室 上海200011;2.中国船舶及海洋工程设计研究院 上海2000113.上海船舶研究设计院 上海201203)
引 言
安装于水线以下船体表面的附属体(如侧推孔、舵、减摇鳍、轴包套、轴及轴支架等)统称为船的附体,由于附体的存在而产生的阻力称为附体阻力[1]。目前比较常见的计算方法是通过全附体与裸船体船模试验所得到的总阻力的差值来确定附体阻力。但由于船模速度低、附体尺度小,故存在较严重的尺度效应[2]。水下附体阻力主要为黏压阻力和摩擦阻力,雷诺数是其尺度效应的重要影响因素。此外,考虑船尾伴流场的尺度效应是非常必要的,历届ITTC会议均十分关注这个问题。第26届ITTC 伴流场尺度效应专门委员会[3]还系统地总结了目前存在的几种换算法。
CFD就是针对目标船型利用计算机进行数值计算,从而得到船舶阻力等的计算方法。CFD是船舶计算流体力学的一个分支,也是船舶流体力学最基本的应用[4]。目前理论上进行实尺度船舶附体数值计算已经成为可能,只是缺乏实船验证数据[5]。
目前国内外已有众多学者对船舶尺度效应开展了相关研究。张恒和詹成胜[6]计算了KCS(KRISO Coutainer Ship;其中: Korea Research Institute for Ships and Ocean Enginearing,KRISO)在不同雷诺数下的阻力值,证明通过改变介质的黏性系数使得不同尺度船舶满足全相似是可行的。陈骞等[7]计算了静水下实尺度船舶不同航速的总阻力,并通过水池试验验证了实尺度模拟、优化的可行性。王展智和熊鹰[8]计算了DTMB5415多种尺度的船舶黏性流场,详细分析了该船轴向伴流场的尺度效应。Bart Schuiling[9]采用数值方法研究了伴流场的尺度效应。李亮和王超[10]开展了KCS考虑自由液面的实船自航试验数值模拟。
本文采用CFD商用软件NUMECAFineMarine数值模拟,基于RANS(Reynolds Average Navier-Stockes)方法,采用 VOF(Volume of Fluid)方法捕捉自由液面,通过采用动网格刚性变形结合加权变形来处理船舶直航引起的升沉和纵倾浮态变化[11];开展了轴支架双桨船附体尺度效应数值模拟并与模型试验及其实船换算结果对比,分别分析了侧推孔、轴包套、轴支架阻力性能及附体压力分布的尺度效应;同时简要分析了轴支架双桨船的自由液面波形和轴向伴流尺度效应。
1 数学模型和数值方法
取尾垂线和基平面交点为原点,从船尾指向船首为x方向,船宽左舷方向为y方向,z方向垂直向上,形成右手坐标系,见图1。

图1 坐标系和计算模型
对于非定常、不可压的黏性流体,采用流动的控制方程为RANS方程:
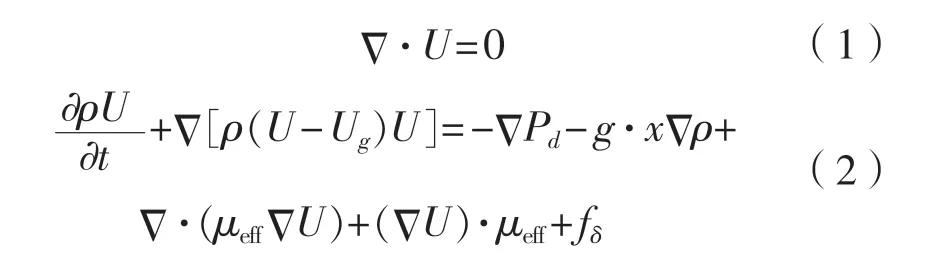
式中:U和Ug分别为流场速度和网格节点速度,m/s;Pd为流场动压力,Pa;μeff为动力黏性系数;fδ为表面张力,N/m3。
2 模型尺度数值模拟及试验验证
本文以某型轴支架双桨船为研究对象,采用计及姿态的阻力和伴流数值模拟方式,数值模拟并分析了轴支架双桨船型阻力与伴流尺度效应分析。表1为某型轴支架双桨船部分船模主尺度。

表1 船模A主尺度
针对阻力数值模拟,在HEXPRESS软件中生成高质量六面体非结构化网格,整个计算域与船体表面网格如图2所示。
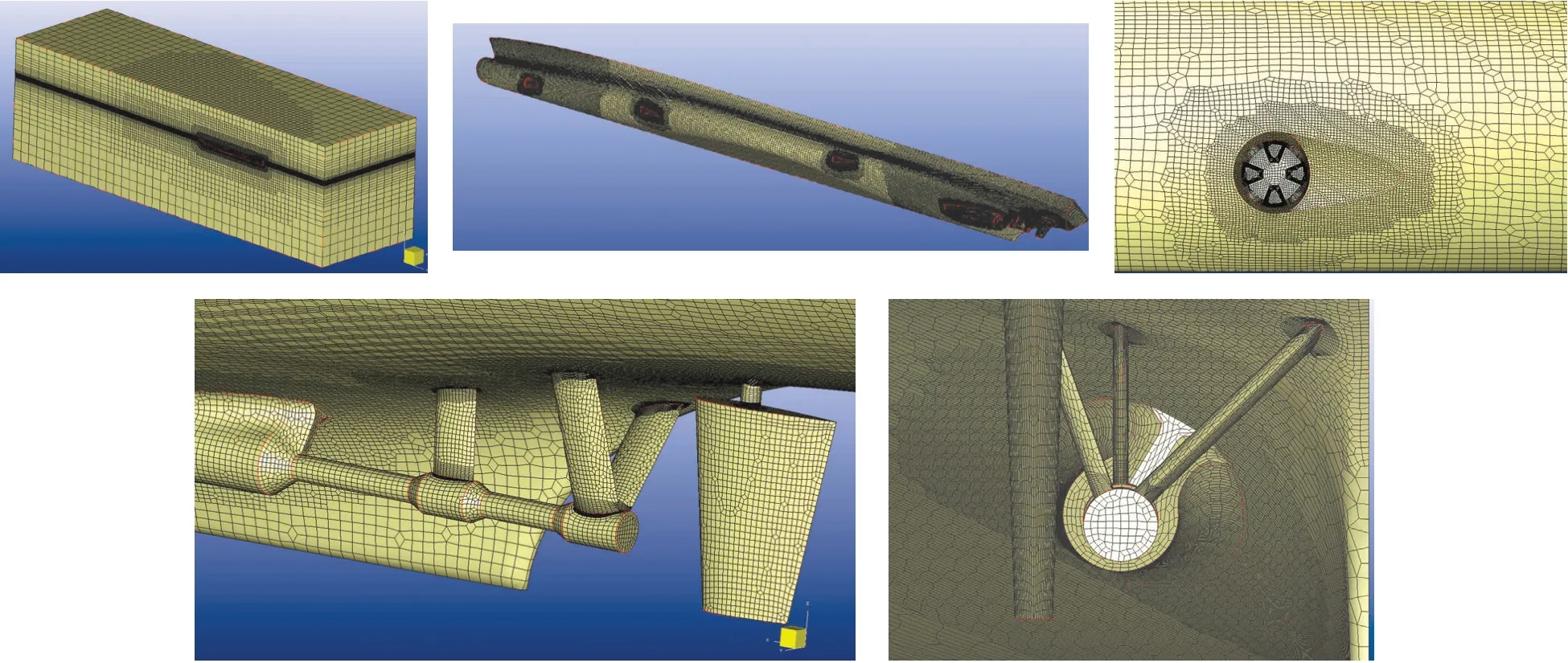
图2 计算域及船体表面网格
计算设置船体纵倾和沉降为自由变化,输入船体浮心坐标(以浮心替代重心作为转动中心)、重力、绕y轴的惯性矩[12]。
该计算域的长度为5倍船长,宽度为1.5倍船长,高度为1.5倍船长。
在侧推孔、支架、舵等附体采用逐层细化的全六面体非结构网格生成技术,并在侧推孔、支架、舵等附体表面采用拆分紧邻物面一层网格单元的方法生成适当层数的边界层网格[11]。
首先对该轴支架双桨船进行静水中的裸船体和全附体(包括侧推孔、轴包套、支架、舵等附体)阻力数值模型模拟和试验验证,模型试验照片见图3。

图3 模型试验照片
模型尺度(雷诺数Re=1.1×107)阻力计算和模型试验换算成实船的有效功率Pe对比结果见下页图4。

图4 船模计算与试验Pe对比
可见,无论是裸船体还是全附体计算,均与试验结果吻合良好,故可以此计算方法为基础,考虑尺度效应的数值模拟与分析。由于该轴支架双桨船附体种类和数量多,因此其全附体阻力的增量偏大。本文中的阻力增量百分比均为与CFD计算中雷诺数为1.1×107时裸船体有效功率之比的增量。
在模型尺度裸船体和全附体数值模拟的基础上,通过改变船模长度的方法,本文分别对“裸船体”、“裸船体+侧推孔”、“裸船体+侧推孔+轴包套”、“裸船体+侧推孔+轴包套+支架”进行了不同雷诺数下的模型数值模拟,并进行附体阻力增量尺度效应分析。
3 阻力、附体压力分布尺度效应分析
本文对不同尺度的阻力、伴流数值模拟生成不同厚度的边界层。表2为不同雷诺数(Re)时的Y+,图5为船体模型尺度流线图。从图5可见,船体表面流动顺畅,无明显的流动分离和汇聚现象,从而为不同附体阻力增量的尺度效应分析提供良好的基础。

图5 船体流线图

表2 不同Re下的网格Y +
图6为不同Re阻力数值模拟结果对比;下页图7为不同Re下各附体Pe增量对比。不同尺度的数值模拟都采用淡水的密度和黏度,同时并没有在数值模拟中考虑表面粗糙度的差异,而是在换算过程中统一标准补偿此差异。
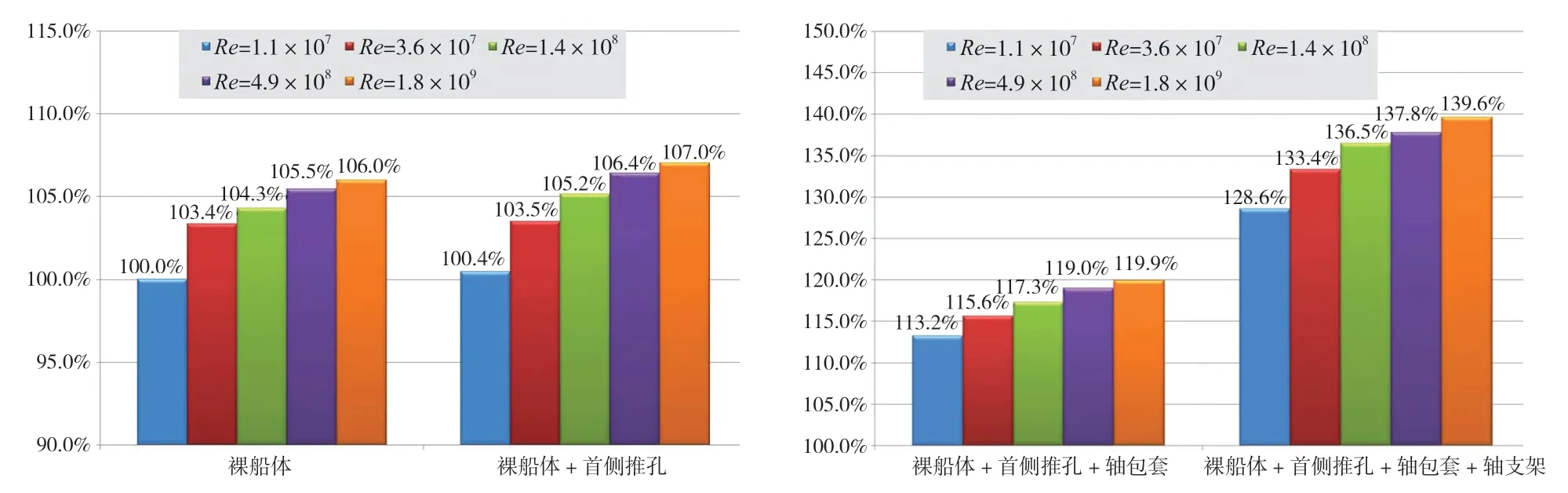
图6 不同Re阻力数值模拟结果对比
从图6和图7中可见,无论是裸船体还是裸船体+附体阻力计算,Pe结果均随Re的增加而增大。这一增量在Re为107量级上最快,随后趋于平缓。3种附体的阻力增量均不随Re的增加而单调变化,但在Re>108以后基本趋于稳定。侧推孔和轴包套随Re增加,但阻力增量变化很小,均在1%以内;轴支架的阻力增量在Re为107~108时,与裸船体相同,增加均很快。
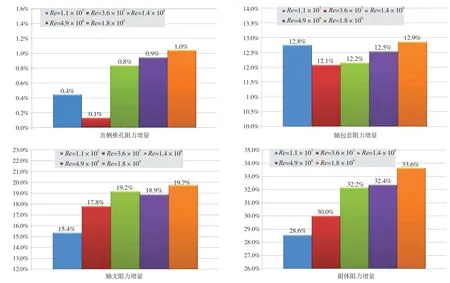
图7 不同Re的附体Pe增量对比

续图8 不同附体压力分布数值模拟结果
下页图8为轴包套和支架不同Re下的无量纲压力分布。从图中可见,轴包套折角处收缩较为剧烈,此处存在一个负压较大的区域;且这一区域的面积和绝对数值均随Re增加而明显增大。双臂外支架的外侧处大片的负压区域是支架阻力增量很大的原因,当Re为107~ 108时,负压区域面积增加明显。这与图7中支架阻力增量随Re变化关系相对应。
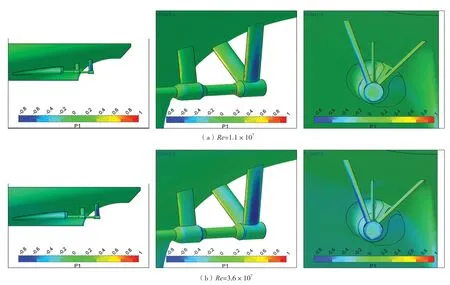
图8 不同附体压力分布数值模拟结果
4 兴波、伴流尺度效应分析
在阻力尺度效应分析的基础上,进一步开展轴支架双桨船兴波和伴流的尺度效应分析。下页图9为“裸船体+侧推孔+轴包套+支架”在不同雷诺数无量纲自由液面的数值模拟结果。由图9可见:不同雷诺数船体中前部分的兴波差异很小,这同兴波阻力与Re无关的假设相符,但在船尾后方波形存在一定的差异,这与船体傅氏数及尾封板浸水深度相关。
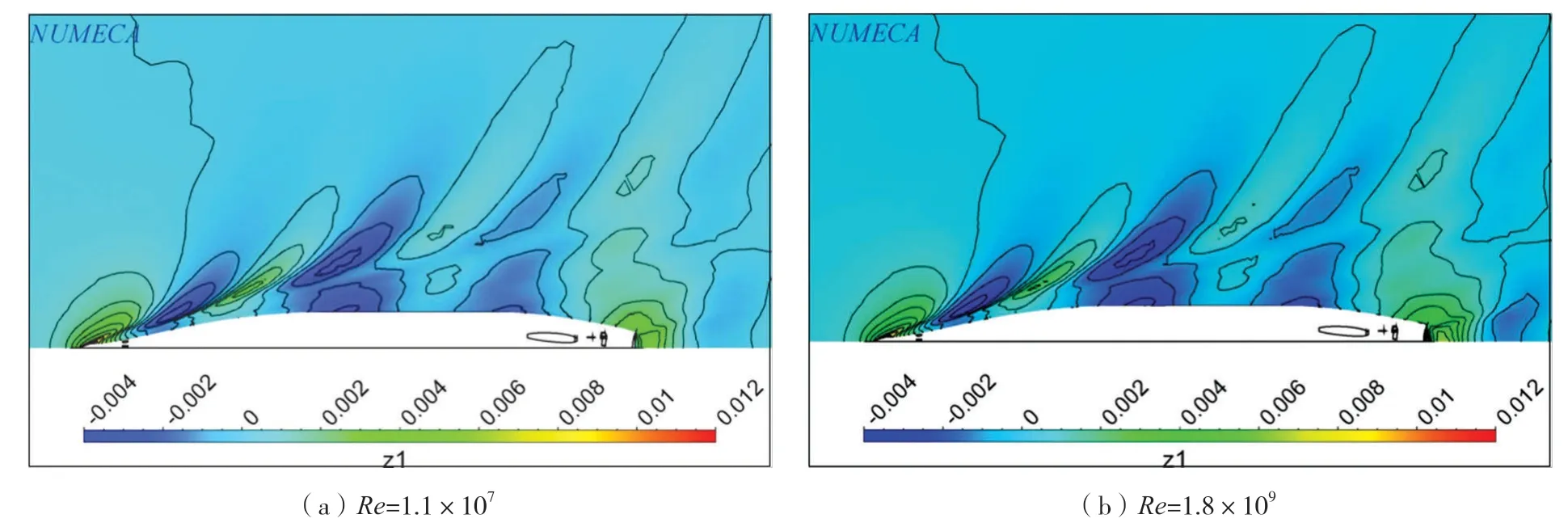
图9 不同Re自由液面数值模拟结果
下页图10为不同Re桨盘面(0.35R~1.2R)伴流数值模拟结果(左舷)。由图10可见,轴向伴流顺时针30°区域存在一片伴流较高的区域,可能是后视图中包套和内支架联合影响的结果。高雷诺数数值模拟结果表明:高伴流区域的伴流峰值显著降低,其他低伴流区域面积随着Re的升高显著增大。
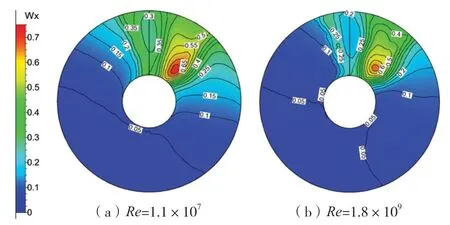
图10 不同Re伴流数值模拟结果(左舷)
5 结 论
本文使用NUMECAFineMarine软件研究轴支架双桨船尺度效应,研究发现:
(1)由于附体区域的局部Re远远小于船体Re,当船体Re大于108之后,3个附体的阻力增量才基本稳定。为了减小尺度效应影响,轴支架双桨船模型试验的Re应尽可能大些。
(2)不同Re船体中前部分的兴波差异很小,但在船尾后方波形存在一定差异。这与船体傅氏数及尾封板浸水深度相关。对于轴支架双桨船,桨盘面轴向伴流均值和伴流峰值都随Re增加而降低。
