基于SPARK GraphX的YELP社区发现研究

袁丽娜 王红勤 潘正军

（广州软件学院软件工程系 广东省广州市 510990）

随着互联网的快速发展，网络分析逐渐成为研究热点，而社区发现是复杂网络研究中的重要领域。在这大数据时代，分布式计算平台在大数据处理领域发挥着举足轻重的作用，使用分布式计算平台不仅能够快速处理海量数据，还能提高算法的执行效率，在实际生产中起着非常重要的作用。Hadoop 和Spark 是目前主流的开源分布式处理平台。本文重点研究使用Spark GraphX 对YELP 数据集进行社区发现及可视化。

1 社区发现

1.1 复杂网络

现实世界中，每个个体或者事物都至少属于一个系统中，不同的个体之间通过各种方式进行着交互，如社会关系、万维网、交通运输系统等，若将这些个体看成一个个节点，个体间的交互关系看成边，即可将这些高度复杂性的网络抽象成为一个复杂网络。复杂网络理论的研究最早来自于1736年数学家欧拉关于七桥问题的解决，进而哈佛大学心理学家通过“六度分离”理论研究了人与人之间的社交关系网络图，从此复杂网络正式进入了全新的领域。而对于复杂网络的研究最具开创性的文章主要有两篇，其一为1998年6月在Nature 杂志上发表《“小世界”网络的集体动力学》的文章；其二为是1999年10月在Science 杂志上发表的《随机网络中标度的涌现》的文章。后续复杂网络在学术界开始进行大量研究[1]。

复杂网络区别于正常普通网络主要表现在网络规模庞大，节点种类繁多，结构复杂，连接多样化、具有动态性等[2]。

复杂网络在探索其网络拓扑结构中，主要涉及以下统计类指标：

（1）度及度的分布：某节点的度指的是与该节点直接相连的节点总数。有向网络度分布包括出度、入度两种特征，从不相关节点到连接相关节点之间通过边连接，这种边的总数量称为入度；从目标节点到其它节点的边的总数称为出度。复杂网络中，描述节点度分布状况的函数是度分布函数。

（2）平均最短路径：连接两个不同节点所需最少边的数量称为两节点之间的最短路径。而任一节点到其余节点的平均距离叫做平均最短路径，通常用来描述网络的大小和节点及节点是否紧密联系。

（3）聚类系数：一个节点能够连接的邻居节点之间实际存在的边数与最大可能边数之比称为聚类系数，通常用来描述网络中一个节点的聚集程度。

（4）介数中心性：介数中心性是基于最短路径的，用来衡量网络图的中心性。介数分为节点介数和边介数。节点介数可以通过网络中经过某节点的最短路径的数目除以所有最短路径数目计算得到。边介数可以通过网络中经过某条边的最短路径的数目除以所有最短路径数目得到[3]。

复杂网络发展不断演化，网络拓扑结构的发展从开始的规则网络模型、随机网络模型，然后到小世界网络模型、无标度网络模型等。

（1）规则网络。规则网络是指网络中任意两个节点之间通过既定的规则进行连接，各个节点的邻居节点数目相同。常见的包括全局耦合网络、最近邻耦合网络和星型耦合网络。

（2）随机网络。随机网络即指网络当中的任意节点不是按照确定的规则连线，而是使用纯粹的随机方式进行连线。如果节点按照某种自组织原则方式连线，将演化成各种不同网络。

（3）小世界网络。规则网络和随机网络两个极端并不能完全展示真实网络的相关特征，而小世界网络模型则作为两者的过渡。

无标度网络。很多网络中其实只有少数节点与大量节点之间存在链接关系，在度分布上具有幂律形式，而多数节点则是存在极少数几个链接，这些具有大量链接的节点称为“集散节点”，所拥有的链接数可能高达几百、几千甚至几百万。无标度网络就是包含这种集散节点的网络，且网络节点的度没有明显的特征长度。

1.2 社区发现

科学家们根据图论理论对现实网络构建了大量数学模型，通过这些模型发现了其相似的规律及特征，因此社区结构被发现成为了网络存在的重要特征。同一社区具有一定的共性信息，社区内部连接紧密，社区间连接稀疏。社区发现属于挖掘复杂网络社区结构的技术，实际上是一种网络聚类的方法，即可以将其理解为一类具有相同特性的节点的集合。复杂网络中的社区结构分析不仅可以得到网络结构特点的统计结果，也可以了解网络的动态特性。有效的社区结构挖掘在很多领域都有非常重要的意义，例如交通网络中，通过社区发现，可以帮助交通部门分析不同路段车流量的情况，从而合理地规划网络中交通灯的变化情况；也可以通过社区发现，快捷地捕获到用户感兴趣的信息，实现热点挖掘、个性化推荐和链接预测；还可以为经济、政策及社会活动提供导向性作用，预测传染病传播等各方面。复杂网络的社区发现在政治、医学、经济、生物学和社会关系等领域均获得广泛关注[4]。

近几年社区发现发展快速，目前，已经有一些算法被提出来用于社区发现，这些算法从不同的角度出发，在不同的网络上进行模拟实验，研究了不同类型的社区结构，同时也提出了模块度等衡量社区质量的指标。按照社区结构来划分社区发现算法，通常可以分为重叠社区发现算法和非重叠社区发现算法。按照算法检测的网络来划分，通常分为可以应用在无向网络、有向网络、符号网络以及无符号网络的社区发现算法。社区发现算法主要包括基于图分割的Kernighan‐Lin 算法，基于层次聚类的GN 算法，基于模块度优化的贪婪算法，模拟退火算法，半监督聚类的标签传播算法等。

2 SPARK GraphX

Apache 下的顶级开源项目Spark，是一款专门为快速处理大规模数据而设计的计算引擎，如今已经形成了一套完整的生态系统，在此生态系统中既可以提供内存计算框架进行大规模数据计算，也可以使用Spark SQL 提供SQL 即席查询，使用GraphX 进行图计算和处理，使用MLlib 机器学习，使用Spark Streaming 对流数据进行流式计算。

Graph X 属于Spark 生态系统中的子项目，主要用于进行分布式图处理，实际上就是图算法的并行化实现，将大图分割成一个个子图，然后放在分布式集群上并行化处理。Graph X 利用Spark 为其图的计算引擎，同时很好地融合其他Spark 生态系统中的组件，实现了大规模图计算的功能[5]。

3 YELP社区发现研究

Yelp 是美国最大点评网站，于2004年创建，包括各种商户，其中涵盖各地餐馆、酒店、购物中心、旅游等各领域，网站的用户则可以在Yelp 网站中交流各种购物实践体验，给体验过的相关商户进行打分评论等。在Yelp 网站中可以通过名称等查询某个酒店或餐厅，则可以看到酒店或餐厅的简要介绍及网友的星级评价和各种体验评论。通过各种体验评论用户则可以对酒店或餐厅有更直观的了解。因此用户在获取信息的需求之外，也有获取服务的需要。本文对Yelp 社交网络三万多条用户信息数据集进行分析，以Spark为平台，使用Spark GraphX 为工具，进行大规模的并行图计算。关键实现代码如下：

经计算分析，虽然有三万多条用户信息，但有些用户之间没有任何交集，本文通过sparkGraphX 根据图的连通性将这些具有连通性的所有顶点及边构建出来，共3565 个顶点，分别用各种颜色的点表示，边用白色表示，其社交网络图如图1所示。

图1：有关联用户的社交网络图

并且将此3565 个相关用户的重要属性数据抽取出来，计算出每个顶点的度，然后根据度的大小进行倒序排序，如图2所示。

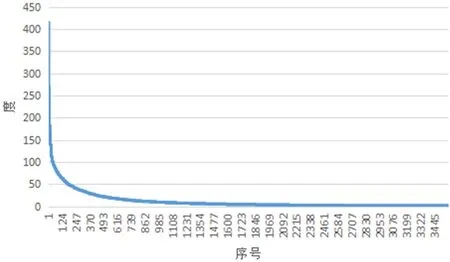
图2：用户度中心度的幂律分布图

通过图2 可以看出，其符合幂律分布规律，因此该社交网络属于复杂网络中的无标度网络结构[6]。该Yelp 社交网络中只有极少数的用户和非常多的用户有关联，而大部分用户只和少部分的用户存在关联关系。通过了解其社交网络结构，对于该网络中重要用户的度量及相关研究都有重要的作用。

4 结束语

本文重点研究了复杂网络中的社区发现问题，并采用Spark GraphX 对YELP 数据集进行社区发现实现及可视化。YELP 社交网络属于复杂网络中的无标度网络结构，其特征是网络中的大部分节点只和很少节点连接，其社区结构的发现对于后续研究其社交网络中信息传播具有一定的实际意义。