基于最近邻数据关联的车辆多目标跟踪

毕栋 邱子威

（湖北汽车工业学院汽车工程师学院 湖北省十堰市 442002）

车辆多目标跟踪是对传感器感知的到的信息进行计算与分析，通过确定目标的位置、加速度、速度、位姿等运动参数，并持续估计车辆所在区域，最后实现目标轨迹的跟踪。目前多目标跟踪算法研究框架主要基于检测跟踪和基于深度学习这两种框架[1‐2]，传统的数据关联算法有最近邻数据关联算法[3]、概率数据关联算法[4]、联合概率数据关联算法[5]等。

最近邻数据关联算法（Nearest Neighbor Data Association，NNDA）最早是由SINGGR 等1971年提出的简单有效的数据关联方法，该方法主要就是要解决关联门的大小和关联门内目标匹配这两个问题，关联门就是以上一帧的跟踪目标为中心划分的空间区域。NNDA 算法简单、计算量小并且易于实现，但在目标比较密集的情况下，算法容易出现对检测目标误检和漏检的情况。后来很多学者针对NNDA 算法不足做了一些改进，胡朋启[6]基于最近邻数据关联算法提出了一种最近邻‐点拓扑图的目标关联算法，该算法有效地克服了最近邻方法对系统偏差敏感，显著提高了存在系统误差条件下的关联成功率。

本次研究建立了基于多传感器融合的车辆多目标跟踪系统，可实现复杂场景下的多目标跟踪，有效融合数据关联算法快速获取可靠的轨迹数据。实验结果分析，本文算法可以有效解决目标遮挡、漏检的问题，并很好地获取实时目标轨迹，为智能驾驶提供可靠的轨迹数据。

1 多目标跟踪关联实现

在复杂交通场景下，车与车之间有较高的相似性和交互性，这使得多目标跟踪难度剧增，其主要是在解决检测目标集与已形成轨迹集关联匹配问题的同时，算法也要保证匹配精度和实时性。

本次研究采用最近邻关联算法，在检测目标的同时根据当前帧实时更新状态轨迹，大大提高匹配精度和实时性。利用激光雷达和摄像头获取输入序列的检测结果，从第k 帧的检测结果开始，计算目标检测集与前一帧已形成轨迹集之间的关联矩阵，结合关联判定准则得到三种关联结果，最后结合卡尔曼对目标轨迹预测及更新，实现目标轨迹的持续跟踪。

数据关联多目标跟踪过程如图1所示。

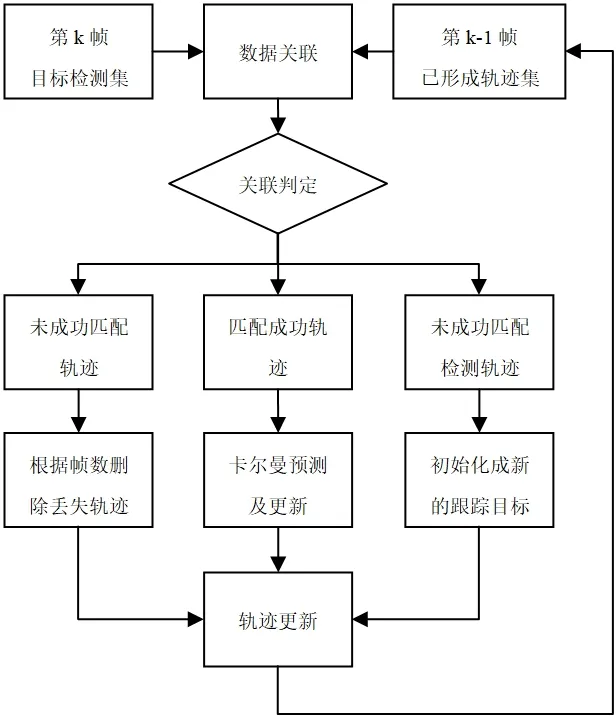
图1：数据关联多目标跟踪过程

最近邻数据关联主要分为两步，第一步是检测每帧中移动的目标，第二步是通过计算损失函数将检测到的目标与之前正在跟踪的同一目标进行关联。损失函数阈值大小直接影响检测目标与已形成轨迹之间的关联概率，因此损失函数阈值大小既要使真实检测目标计算的损失函数小于阈值，又要减少无关的检测结果，损失函数阈值大小可以根据跟踪场景的情况进行相应调整。在确定了损失函数阈值之后，车辆多目标跟踪系统将统计距离最近作为目标检测集与已形成轨迹集之间的判定准则。

在跟踪目标i 的损失函数阈值之内，将检测结果j 与目标航迹预测位置i 这两者之间的矢量差定义为残差[7]，表示为：

设Sij为残差信息的协方差矩阵，于是可以得到统计距离平方值：

该值是判断“最近邻”的度量标准，利用先验信息的最大似然概率。假设残差服从零均值多维正太分布，则残差的似然函数为：

近年，学生素养教育方面的问题成为高校人才培养和思想政治教育工作中存在的一个较为突出的问题，而职业素养，对于学生求职、就业都起着至关重要的作用，也是大学培养体系不可缺少的部分。目前大学生大多为95后，独生子女，家庭溺爱下成长，自主学习能力较差，职业素养相对欠缺。作为应用型院校，培养的毕业生大多去企业工作，而企业对员工的品质、综合能力、职业素养越加重视，这就要求大学生不仅要具备较高的理论素养，更要具备实践能力及职业素养。

由公式（3）可知，先对其取对数，然后再求导，可计算得到最大似然函数值。于是就能得出残差似然函数极大值与残差极小值具有等效关系，它们分别使用gij与eij表示。为此在具体场景中，只要选取距离最近的检测结果即可。

假设由检测器得到的轨迹集合和检测目标集合，p 表示第t 帧中第i 个检测目标，q 表示第t 帧中第j 个检测目标，将巴氏距离作为相似性度量：

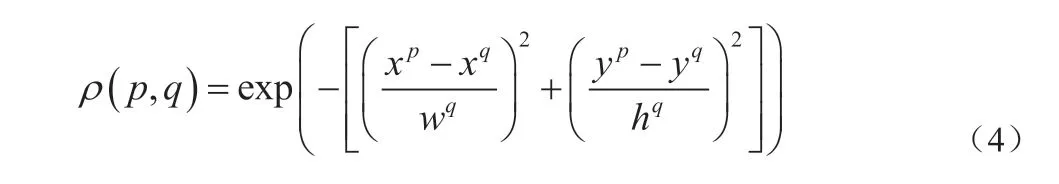
式中，xp和xq分别为p 和q 的横坐标；yp和yq分别为p 和q的纵坐标；wq和hq分别为检测目标的宽和长。

2 轨迹处理

2.1 关联结果处理

根据关联判定准则最终三种关联结果，其分别为：检测目标与前一帧轨迹匹配成功；前一帧轨迹集中的轨迹未与检测目标集匹配成功，目标在当前目标检测集中丢失，可能是目标漏检或者目标离开当前检测范围；目标检测集中的检测目标未与前一帧轨迹集匹配成功，这可能是当前帧中出现一个新的跟踪目标。针对以上三种关联结果，检测目标集和前一帧轨迹集的处理分为以下四种方式：

（1）检测目标与前一帧轨迹匹配成功，则将检测目标作为新轨迹进行卡尔曼预测并更新，对目标进行持续跟踪。

（2）设定跟踪目标连续不可见帧数阈值n，如果跟踪目标连续不可见帧数小于阈值，则认为目标检测算法存在漏检或者短时遮挡，需要将检测目标重新并入轨迹集中，然后根据目标信息进行位置预测。如果跟踪目标连续不可见帧数大于阈值，则认为跟踪目标超出目标检测算法检测范围，删除当前帧中此轨迹信息，不再对其进行预测和更新。

（4）设定两跟踪目标出现遮挡时的距离为l，当跟踪目标出现遮挡，持续对其进行位置预测，当目标检测算法再次检测到跟踪目标时，重新关联匹配并更新到轨迹集中。

2.2 基于卡尔曼滤波遮挡处理

在包含各种不确定信息的动态系统中，如目标遮挡，卡尔曼滤波依靠运动信息可以很好的对下一帧目标所在位置进行预测，即便存在诸多干扰卡尔曼滤波也能得到接近真实目标的预测位置。在目标的状态短时间内不会发生剧烈变化的情况下，将目标速度、加速度、位置视作目标状态矢量，借助于动力学方程来对其状态变化进行描述，然后通过递推算式预估出目标状态。卡尔曼滤波可以借助观测结果对系统状态进行最优估计，主要通过检测与校正这两步来完成目标位置的估计，在预测阶段使用上一帧跟踪目标的位置和状态做出对当前帧目标的位置预测，在校正阶段利用当前帧的检测结果状态来修正预测阶段得到预测位置。

由k‐1 时刻到k 时刻，系统状态预测方程及状态观测方程为：

式中，A 表示状态转移矩阵；uk表示系统输入向量；B 表示输入增益矩阵；wk表示均值为0，协方差矩阵为Q，且服从正太分布的过程噪声；H 表示测量矩阵；vk表示均值为0，协方差矩阵为R，且服从正太分布的过程噪声。

通过上一状态的最优值和将要施加的控制量来预测当前状态，而高斯噪声均值为0，可以省略式（5）最后一项得到：

式中，xk为卡尔曼估计值。

卡尔曼滤波本质是最小均方差估计，而均方差是Pk的迹，协方差矩阵求迹并两边对卡尔曼增益Kk求导，可得卡尔曼增益：

最后更新估计误差的协方差矩阵：

以此迭代并更新计算，完成目标位置的持续跟踪。卡尔曼滤波适用于连续变化的系统中，由于仅需保存前一帧的轨迹集，所以算法运行速度较快，使车辆多目标跟踪系统有较好的实时性。

3 实验仿真与分析

本次实验以MATLAB 为仿真平台，首先通过代价矩阵计算对关联结果进行判定，然后将匹配成功的轨迹用卡尔曼滤波进行更新，未匹配成功检测轨迹更新成新的跟踪目标，设定不可见帧数阈值为20，新目标连续出现帧数阈值为3，两跟踪目标出现遮挡时的距离为1.5m，最后综合初步确定跟踪轨迹。MATLAB 多目标跟踪仿真如图2所示。

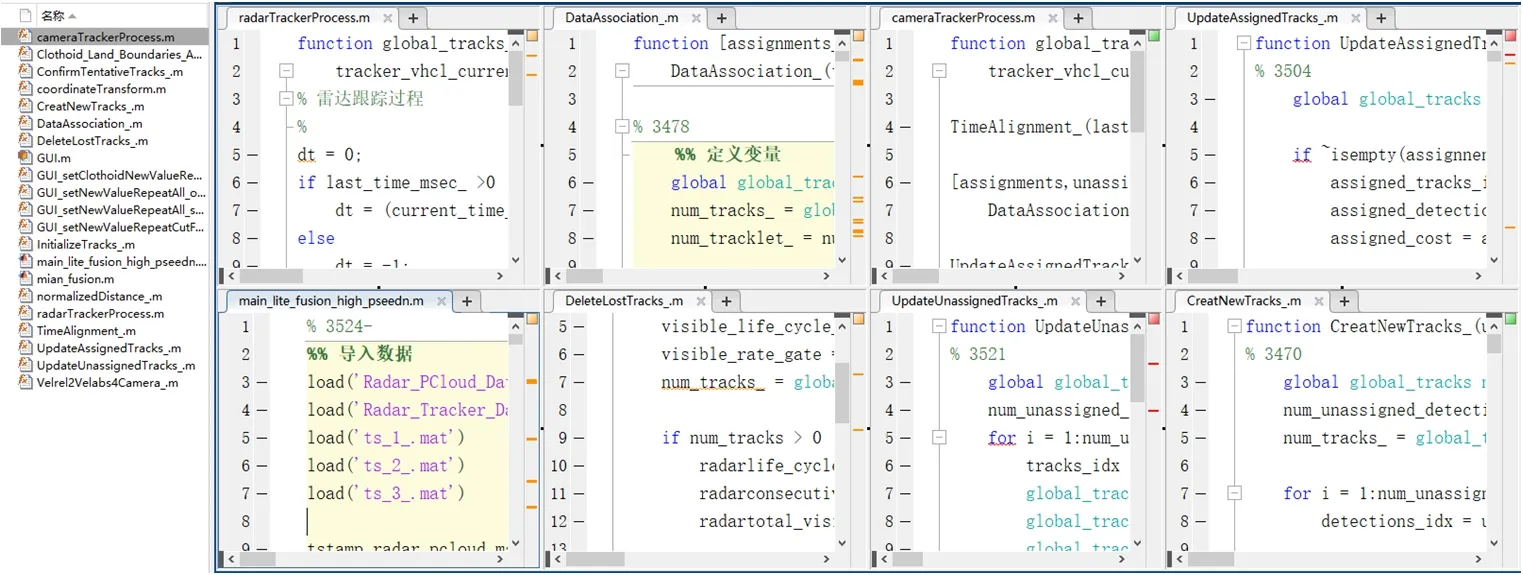
图2：MATLAB 多目标跟踪仿真

仿真结果在GUI 显示界面中显示，红色三角表示自身汽车位置，绿色方框及箭头表示摄像头跟踪目标位置及行驶方向，黄色方框及箭头表示激光雷达跟踪目标位置及行驶方向，紫色方框及箭头表示数据关联后目标位置及行驶方向。图3 为连续两帧汽车多目标跟踪仿真。

图3：MATLAB 多目标跟踪仿真

仿真结果显示本次研究的算法能够实现车辆多目标的跟踪，可以实现连续多帧良好的跟踪效果，并且在行驶过程中，2 号目标和3 号目标短暂遮挡也能通过算法进行识别跟踪。

4 结论

本次研究利用最近邻数据关联算法来匹配检测结果与跟踪目标，首先根据统计距离进行关联判定，然后结合卡尔曼滤波器的目标遮挡模型，利用卡尔曼滤波更新快，能快速构造预测位置的特点，有效解决短时遮挡问题，多目标跟踪系统的鲁棒性得到显著提高，最后利用多帧信息对跟踪目标持续跟踪，使关联算法更稳定。多组测试序列检测结果表明，本文的跟踪算法可以满足实时性的要求，可应用到实际工程中，下一步工作重点是提高准确率。